§ 2. Резонатор в безграничной стенке

123

Перейдем теперь к расчету резонаторов. Рассмотрим три случая:

а) резонатор в безграничной стенке;

б) перфорированные экраны перед жесткой стенкой;

в) случай нескольких резонаторов.

§ 2. Резонатор в безграничной стенке

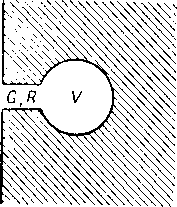
Пусть на безграничную стенку, в которой имеется один резонатор, нормально падает плоская волна. Пусть G —проводи­мость резонатора, V — его объем,, a R — сопротивление (фиг. 74). Последнее является мерой затухания ре­

зонатора и будет определено ниже.

Поглощение и рассеяние звука резо­натором полностью описываются его импедансом Z, зависящим от частоты. Импеданс Z определяется как отноше­ние звукового давления р к объемной скорости v; его можно выразить через

\G, $ и V

z

^-+$ +

*Ро /«>V •

(7.4)

/1

'/ Фиг. 74. Единичный

Это уравнение выражает тот факт, резонатор,

что часть внешнего давления идет на А.

преодоление инерции и сопротивления трения наЩдящегося в канале воздуха; остальная же часть идет на адиабатическое сжатие воздуха в полости. В электрических аналогиях такая систе­ма соответствует последовательному соединению элементов цепи. Для цилиндрического канала слагаемое, обусловленное инерцией (без поправок на концы), равно j^₀l/S. Согласно Рэлею, оно мо­жет быть представлено в общем виде j^jG для случая, когда канал не цилиндрической формы и когда учтены поправки на открытые концы. Так как р включает в себя влияние инерции воздуха перед резонатором, то оно не является давлением точно у входа в канал, но представляет собой давление перед резона­тором на некотором расстоянии от входа, например на рассто­янии, равном диаметру канала (точка А на фиг. 74). Слагаемое, обусловленное упругостью, вытекает из определения модуля сжатия, который равен *р₀; появляется при дифференцирова­нии смещения по времени (электрический аналог 1//о)С).

Величина очевидно, представляет собой составляющую звукового давления р в точке А, находящуюся в фазе со ско­ростью v и деленную на эту скорость.

Если в точке А амплитуда звукового давления равна р, а

объемной скорости равна v, то поглощаемая мощность будет ¹/г v²R,

Г л. VII. Резонансные звукопоглотители

аналогично выражению I²R = ¹/₂i ²R _в электродинамике; Сможет быть вычислено через р по формуле

Р= \ Z\vy

так что нужно знать только значение р, чтобы найти погло- щаемую мощность.

В вопросе о давлении часто возникают недоразумении. Когда на стенку падает плоская водна с амплитудой p_i9 то давление в точке А не будет равно ни 2 p_iy как вблизи твердой стенки, ни pi, как^считают некоторые авторы, а будет зависеть от сопро- тивления излучения отверстия. Чтобы найти это звуковое давле-

ние, представим себе безинерционный поршень, который может без трения перемещаться в канале. Под действием внешней силы этот поршень будет пе- ремещаться с объемной скоростью v. При наличии падающей плоской волны давление с внешней сторон^ поршня равно сумме 2pi — Z_n3A.v_y 1*де первое слагаемое обусловлено падающей вол- н|й, а второе —излучением; Z_H3JI, есть сопротивление излучения поршня. Дав-

ление с внуЛенней стороны, очевидно, равно Z'v_y где Z' равно Z мийус сопротивление, обусловленное внешней по отношению к поршню массой в канале и равное /о)р₀Д/_Внешн./5. Следователь- но, условие равенства давления с обеих сторон поршня запи- шется в виде:

2pi — Z_waAv = Z'v. (7.5)

Знак минус перед вторым членом в левой части обусловлен тем, что за положительное направление скорости взято направ­ление от внешнего конца канала к внутреннему. При v, удовле­творяющем этому уравнению, не требуется никакой внешней силы для поддержания движения поршня; поэтому в первом прибли­жении мы ничего не изменим, если уберем этот поршень. Следо­вательно, уравнение (7.5), связывающее скорость v и давление па­дающей волны, справедливо для резонатора без поршня. 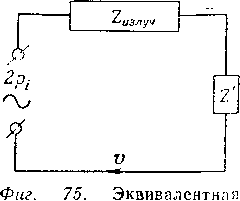На фиг. 75 показана соответственная электрическая схема. К двум последова­тельно соединенным сопротивлениям Z_II3;I. и Z' приложена э.д.с. 2р_{. Сюда приложима известная теорема из теории электричества: ток в любом участке электрической цепи равен току, который про­ходил бы по этому участку, если бы он был присоединен к за­жимам источника тока с э.д.с., равной напряжению на концах данного участка цепи при бесконечном сопротивлении этого

схема для резонатора.