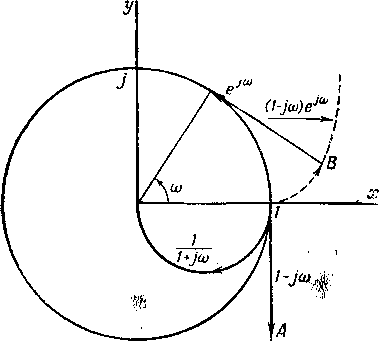- •Глава I
- •§ 2. Импеданс слоя конечной толщины
- •§ 3. Волновой импеданс воздуха
- •§ 3. Волновой импеданс воздуха
- •§ 4. Изображение результатов в комплексной плоскости
- •§ 4. Изображение результатов в комплексной плоскости
- •§ 5. Геометрическое изображение cth у/
- •§ 5. Геометрическое изображение cth у/
- •В плоскости г.
- •Поглощения а0.
- •§ 7. Волновой импеданс среды с внутренним трением
- •§ 7. Волновой импеданс среды с внутренним трением
- •2 Звукопоглощающие материалы
- •§ 7. Волновой импеданс среды с внутренним трением
- •Случай резко селективного поглощения.
- •§ 8. У равнение распространения волн в пористом материале
- •§ 8. Уравнение распространения волн в пористом материале с твердым скелетом
- •Фиг. 15. Потери при колеба ниях, гистерезис.
- •§ 8. У равнение распространения волн в пористом материале
- •Фиг. 16. К понятию структурного фактора.
- •Три образца, обладающие одной и той же пористостью h и сопротивлением о, но имеющие различные структурные факторы k.
- •2) С этим принципиальным высказыванием авторов нельзя согласиться, по крайней мере в отношении материалов с простейшей структурой. (Прим, ред.)
- •§ 9. Постоянная сопротивления с
- •§ 9. Постоянная сопротивления з
- •Глава II
- •Влияние вязкости и теплопроводности на распространение звука в пористых средах
- •§ 1. Распространение звука в цилиндрических трубах и порах
- •§ 2. Расчет плотности при пренебрежении тепловыми эффектами
- •§ Зо упругость воздуха в цилиндре (при пренебрежении вязкостью)
- •§ 3. Упругость воздуха в цилиндре
- •§ 3. Упругость воздуха в цилиндре
- •3 Звукопоглощающие материалы
- •§ 4. Применение теории кирхгофа к распространению звука в цилиндрических трубах и порах
- •§ 4. Применение теории Кирхгофа к распространению звука
- •§ 4. Применение теории Кирхгофа к распространению звука 37 Подстановка (2.25) в (2.17) дает 1л0±ы)_ I q3 (tX2r)
- •§ 5. Применение теории Кирхгофа для пористых сред
- •§ 6. Обсуждение теоретических результатов Корринга, Кронига и Смита 41
- •§ 6. Обсуждение теоретических результатов корринга, #он||а и смита ф
- •§ 9. Опытная проверка теоретических результатов
- •§ 9, Опытная проверка теоретических результатов 47
- •4 Звукопоглощающие материалы
- •§ 1. Пористые материалы с упругим скелетом [13, 14]
- •Первый член в правой части (3.1) представляет собой силу инер- ции, а второй член — силу, с которой воздух действует на ске-
- •§ 2. Бегущие волны в пористой среде с упругим скелетом
- •§ 3. Графическое изображение корней г-уравнения
- •§ 3. Графическое изображение корней V-уравнения
- •С отрицательно
- •§ 3. Графическое изображение корней V-уравнения
- •60 Гл. III. Теория поглощения звука пористыми слоями
- •Акустические штукатурки
- •*) Технические единицы метр—килограмм (масса)—секунда. (Прим, ред.)
- •§ 5. Слой с закрытой передней поверхностью
- •§ 5. Слой с закрытой передней поверхностью
- •5 Звукопоглощающие материалы
- •Фиг. 25. Улучшение поглощения при покрывании поверхности податливого слоя.
- •§ 5. Слой с закрытой передней поверхностью
- •Фиг. 27. Импедансный контур покрытого слоя со слоем воздуха позади толщиной 78 мм. Указаны частоты в сотнях герц.
- •§ 6. Слой с открытой передней поверхностью
- •§ 6. Слой с открытой передней поверхностью
- •§ 7. Упругий слой на подкладке, отличающейся от твердой стенки 71
- •§ 7. Упругий слой, лежащий на подкладке, отличающейся от твердой стенки
- •Глава IV
- •Экспериментальное определение постоянных, характеризующих пористые материалы
- •§ 2. Пористость
- •§ 2. Пористость
- •' Пористый образец
- •Фиг. 30. Прибор Леонарда для измерения пористости.
- •§ 3. Воздушное сопротивление
- •§ 3. Воздушное сопротивление
- •§ 4. Модуль сжатия
- •§ 5. Результаты измерений комплексной упругости
- •§ 5. Результаты измерений комплексной упругости
- •§ 5. Результаты измерений комплексной упругости
- •Глава V
- •Измерение нормального импеданса и коэффициента поглощения
- •§ 1. Введение
- •§ 2. Интерферометр постоянной длины
- •§ 2. Интерферометр постоянной длины
- •Фиг. 33. Интерферометр постоянной длины.
- •Фиг. 34. Общий вид интерферометра постоянной длины.
- •§ 3. Метод Вента а Бсделла
- •Фиг. 35. Разрез микрофона, вмонтированного в стейку трубы интерферометра.
- •§ 3. Метод вента и беделла [36]
- •§ 4. Метод ширины максимума давления вблизи излучателя [27]
- •§ 5. Интерферометры, в которых измеряется реакция на излучатель 85
- •§ 5. Интерферометры, в которых измеряется реакция на излучатель
- •§ 5. Интерферометры, в которых измеряется реакция на излучатель 87
- •§ 6. Практическое определение коэффициента поглощения
- •§ 6. Практическое определение коэффициента поглощения
- •§ 6. Практическое определение коэффициента поглощения
- •8. Геометрический величин d, dVl I.
- •§ 7. Импедансный индикатор гелюка
- •Фиг. 40, Излучатель с антирупором для импе- дансного индикатора.
- •§ 7. Импедансный индикатор Гелюка
- •§ 8. Детали импедансного индикатора
- •§ 8. Детали импедансного индикатора
- •Грамма к фиг. 44.
- •Звуковоглешаюшие материалы
- •Фиг. 49, Скелетная схема импедансного индикатора.
- •Глава VI опытные данные. Сравнение с теорией
- •§ 1. Введение
- •§ 2. Опыты на искусственных образцах
- •Фиг. 50. Образец поглощающей конструкции из стеклянных трубок с наклоном 60°.
- •§ 2. Опыты на искусственных образцах
- •Частоты для случая импедансных контуров фиг. 51.
- •§ 4. Пористые материалы с твердым скелетом
- •Фиг. 53. Образец с искусственными боковыми порами.
- •§ 3. Непроницаемые материалы с высокой упругостью
- •§ 4. Пористые материалы с твердым скелетом
- •Фиг. 55. Импедансные контуры пористых материалов с упругим скелетом:
- •§ БЯюристые материалы с упругим скелетом и открытыми порами
- •§ 6. Пористые материалы с упругим скелетом и закрытой передней поверхностью
- •§ 7. Пористый материал, расположенный на расстоянии от стенки 111
- •§ 7. Пористый материал,
- •§ 7. Пористый материал, расположенный на расстоянии от стенки 113
- •Цифры около кривых указывают толщину зазора.
- •Фиг. 67, Графический способ построения импеданса для многослой- ной системы.
- •§ 7. Пористый материал, расположенный на расстоянии от стенки 115
- •Фиг. 68. Зависимость коэффициента поглощения от частоты для покрытого образца пористой резины толщиной 78 мм при наличии воздушного зазора между стенкой:
- •Фиг. 70. Зависймость коэффициента поглощения от частоты для покрытого образца пористой резины толщиной 78 мм при наличии железной сетки, изображенной на фиг. 69, 6.
- •§ 8. Целотекс с-4
- •§ 8. Целотекс с-4
- •Фиг. 71. Импедансный контур для целотекса с-4. Указаны частоты в сотнях герц.
- •Фиг. 72. Эквивалентная схема для целотекса с-4.
- •Глава VII резонансные звукопоглотители
- •§ 1. Введение
- •§ 1. Введение
- •§ 2. Резонатор в безграничной стенке
- •§ 2. Резонатор в безграничной стенке
- •§ 2Ь Резонатор в безграничной стенке
- •Фиг. 77.1гЗависимость параметров, характеризующих эффективность отдельного резонатора, от внутреннего сопротивления и проводимости g.
- •§ 2. Резонатор в безграничной стенке
- •9 Звукопоглощающие материалы
- •§ 3. Практическое использование конструкций с одним резонатором 131
- •§ 3. Практическое использование конструкций с одним резонатором
- •§ 4. Перфорированный экран перед твердой стенкой
- •§ 4. Перфорированный экран перед твердой стенкой
- •§ 4. Перфорированный экран перед твердой стенкой
- •§ 5. Правила проектирования перфорированных звукопоглощающих покрытий
- •§ 5. Правила проектирования перфорированных покрытий
- •Фиг. 83. Зависимость между проводимостью g, диаметром круглого циЩндрического отверстия d и толщиной экрана /.
- •§ 7. Опытные данные
- •§ 6. Проектирование поглощающих экранов с щелями
- •§ 7. Опытные данные
- •§ 7. Опытные данные
- •§ 8. Комбинации резонаторов
- •§ 8. Комбинации резонаторов
- •§ 8. Комбинации резонаторов
- •Глава VIII
- •§ 1. Введение
- •Реверберационный метод. В этом хорошо известном случае падение звука происходит более или менее диффузно. Трактовка этого случая чрезвычайно трудна [67].
- •§ 2. Наклонное падение на поверхность с локальной реакцией
- •§ 2. Наклонное падение на поверхность с локальной реакцией
- •§ 2. Наклонное падение на поверхность с локальной реакцией 155
- •§ 3. Наклонное падение на поверхность с одним резонатором
- •Литература
- •Цена 8 р. 40 к. (по прейскуранту 1952 г.)
- •Москва, Трехпрудный пер., 9.
11
Индекс
0 у а добавлен для того, чтобы отметить
случай нормального падения.
Полученные
здесь для свободного воздуха формулы
имеют более общую применимость. Уравнения
движения и непрерывности во многих
случаях могут быть записаны точно в
такой же форме, как (1.7)
и (1.8),
хотя при этом постоянные р и К
будут иметь другие, в общем случае
комплексные значения.
Во
избежание путаницы все величины,
относящиеся к свободному воздуху,
в дальнейшем будут снабжаться индексом
нуль, как это, например, сделано в
настоящем параграфе: р0,
До, у0,
с0.
Практически
важным способом применения поглощающих
материалов является непосредственное
укрепление слоя материал; на твердой
стенке. Как было показано в § 2,
импеданс на передней стенке слоя в
этом случае будет
Или,
учитывая (1.10) и (1.11), получаем общее
выражение для Импеданса любого слоя,
укрепленного на твердой стенке,
Исключением
являются лишь некоторые пода?||йвые
пористые
материалы.
Вопрос о вычислении К
и р будет рассматриваться
с
§ 7 гл. I по § 6
гл. II.
Для
понимания смысла таких формул, как
(1.5) и (1.11), весьма
полезно
изображение cth
у/
и других комплексных функций г
от
со
на
комплексной плоскости. Если предположить,
что со
про-
бегает
все значения от 0
до оо, то значения рассматриваемой
функции
в комплексной плоскости будут
располагаться на неко-
торой
кривой. Последняя более наглядна, чем
аналитическая
формула.
Для построения кривой необходимо
отделить действи-
тельную
часть функции от мнимой, т. е. представить
z
в
фор-
ме
z
(<о)
=
х
(со)
-f
jy
(со),
после
чего остается лишь изобразить z
в
плоскости с координатами х
и у.
Примеры:
функция z=l
— /со
в
комплексной плоскости пред-
ставляет
собой прямую, начинающуюся в точке х
=
1,
лежащей
на
действительной оси, и идущую параллельно
оси у
вниз (фиг. 3).
Функция
z
=
е3'*
= cos
со
+■
/ sin
со
изображается
окружностью
единичного
радиуса.
Умножение
комплексного числа на е^
соответствует поворо-
ту
его вокруг начала координат на угол
со.
Так,
при умножении
числа,
соответствующего точке А
(см. фиг. 3), на е3'*
мы
z
~W
cth у/.
(1.14)§ 4. Изображение результатов в комплексной плоскости
§ 4. Изображение результатов в комплексной плоскости
![]()
12
Г
л.
/. Элементарная
теория поглощения звука
получаем
точку В;
очевидно, что £ лежит на развертке
окружности. Следовательно, кривая z
=
(1 — /ш) является разверткой окружности.
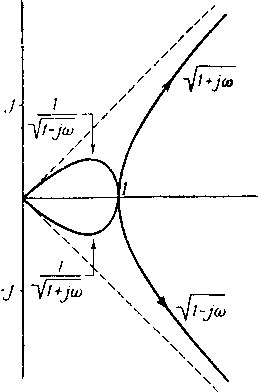
Функция
z
= ]/l +
/«> изображается гиперболой с взаимно
пер- пендикулярными асимптотами (фиг.
4). Действительно, положив z
= x + jy = \/'
1
+ /ш, после возведения в квадрат получаем
х2
__ у2
+
2jxy
=
1
-f
/о).
Приравнивание вещественных частей
дает я2
—у2=1,
что соответствует указанной выше
гиперболе.
Фиг.
3.
Изображение развертки Фиг.
4.
Изображение гиперокружности в
комплексной болы и лемнискаты в ком-
плоскости. плексной
плоскости.
Приравнивание
мнимых частей дает 2хг/ = ш; так как
иГвсегда положительно, то х
и у
должны иметь одинаковые знаки. Отсюда
следует, что функция Hi
+
/<о изображается верхней ветвью
гиперболы, нижняя же ветвь соответствует
функции |/1
— /ш . В более общем случае, когда z
— \Zl ±
//(а>), где /(со)
произвольная
вещественная функция со,
мы
будем иметь ту же самую гиперболу, но
с переменным масштабом для ш.
Обратным
числом для z—МеЯ
является — = -Ге-л>
т. е. мо-
z
М
дуль
является обратной величиной модуля г,
а фаза имеет противоположный знак.
Так как лемниската является кривой,
обратной гиперболе, то она соответствует,
очевидно, функции (1
^ Окружность, как хорошо известно из
геометрии,
является
кривой, обратной прямой линии. На фиг.
3 изображена