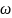РГР4 Гайдук 5А03

Министерство науки и высшего образования Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего образования

«Национальный исследовательский Томский политехнический Университет»

Инженерная школа энергетики

Отделение электроэнергетики и электротехники

Направление: 13.03.02 Электроэнергетика и электротехника

«Расчет переходных процессов в линейных электрических цепях»

РГР-4

Вариант – 185

по дисциплине:

Теоретические основы электротехники

Выполнил: :
студент гр. 5А03			Гайдук К.А.		26.10.2022
Проверил:
доцент ОЭЭ ИШЭ			Шандарова Е.Б.

Томск – 2022

Задание № 4 Расчет переходных процессов в линейных электрических цепях

I. Для заданной схемы при коммутации ключа K₁ в момент времени t = 0, когда ключ K₂ еще не сработал, выполнить следующее:

1. При постоянном источнике ЭДС e(t) = E или тока J(t) = J опреде­лить ток i(t) или напряжение u_J(t):

а) классическим методом;

б) операторным методом;

построить график зависимости тока i(t) или напряжения u_J(t).

2. При гармоническом источнике ЭДС 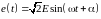или тока 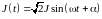определить ток i(t) или напряжение u_J(t):

а) классическим методом;

б) комбинированным (операторно-классическим) методом;

на интервале времени 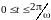построить график зависимости тока i(t) или напряжения u_J(t).

3. При импульсном источнике ЭДС 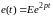или тока 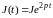и нулевых начальных условиях определить интегралом Дюамеля ток i(t) или напряжение u_J(t), построить их график зависимости (p – корень характеристического уравнения из п. 1, а).

II. Для заданной схемы с постоянным источником ЭДС e(t) = E или тока J(t) = J при коммутации ключа K₂ в момент времени t=0, когда ключ K₁ давно уже сработал, определить ток i(t) или напряжение u_J(t):

а) классическим методом;

б) операторным методом;

в) методом переменных состояния;

построить график зависимости тока i(t) или напряжения u_J(t).

III. Проанализировать методы расчета, результаты вычислений, графики зависимостей и сформулировать выводы по работе.

Исходные данные:

E	J			R	L	C
В	А	град	1/с	Ом	Гн	мкФ
300	5,5	90	600	30	0,1	111

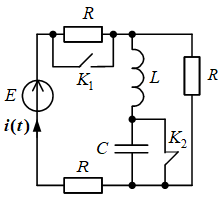
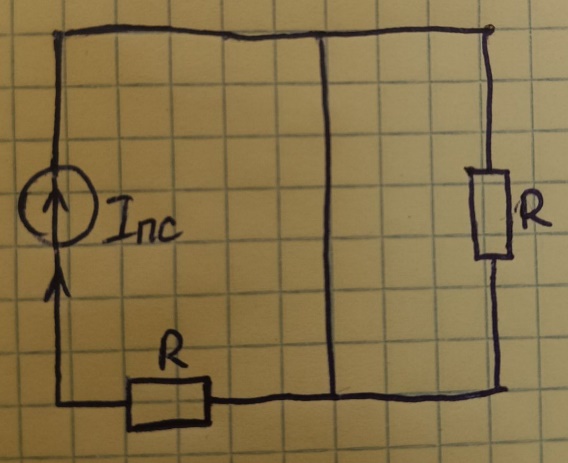
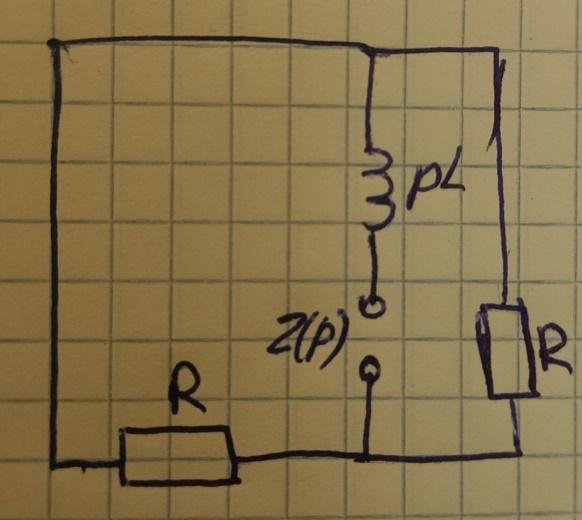
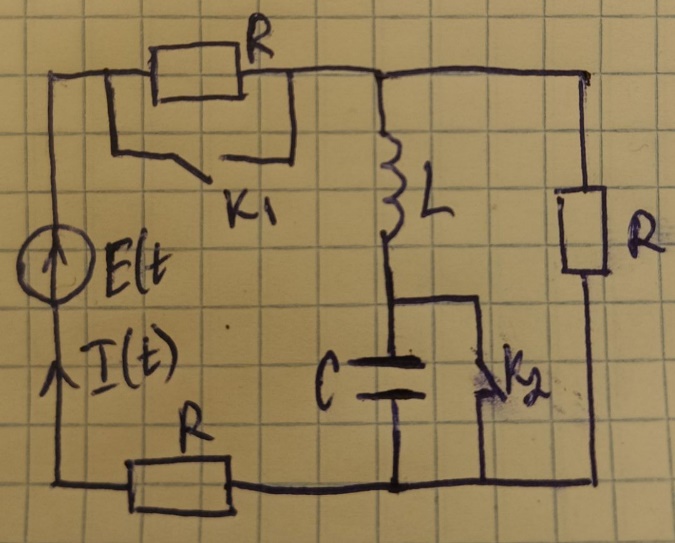
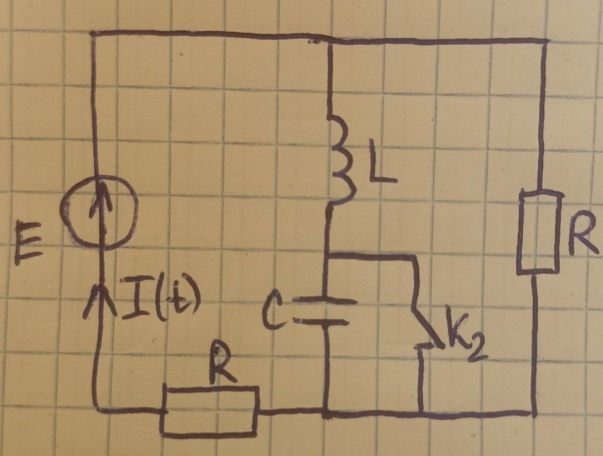
Рис.1. Исходная схема

1.1. Классический метод:

1.1.1 ННУ

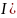
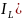
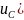
1.1.2 ЗНУ

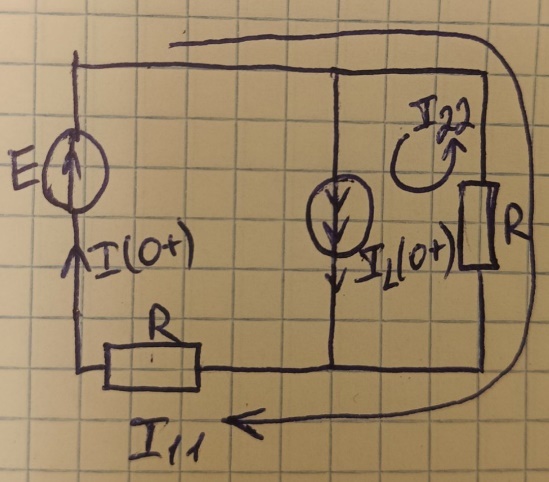
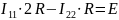–метод контурных токов

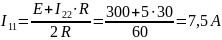
1.1.3 ПС

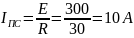
1.1.4 Определим корень характеристического уравнения

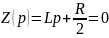
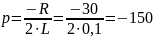
1.1.5 Определим постоянную интегрирования

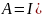
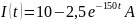
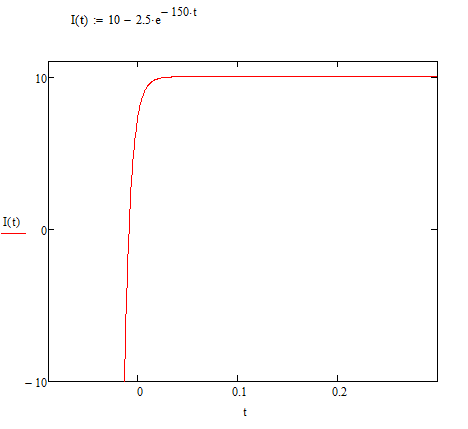
Построим график зависимости i(t)

1.2 Используем операторный метод

1.2.1 ННУ

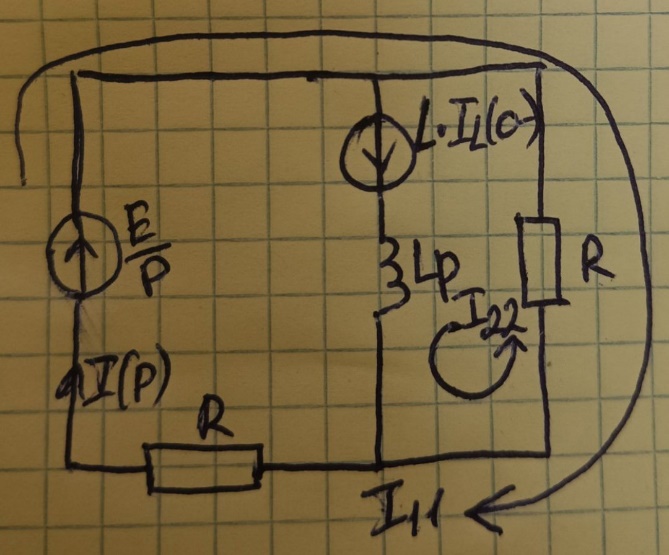1.2.2 Операторная схема после коммутации

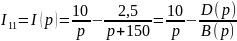
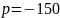
2. При гармоническом источнике ЭДС

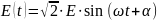
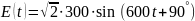
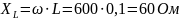
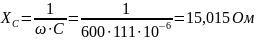
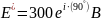
2.1.1 ННУ

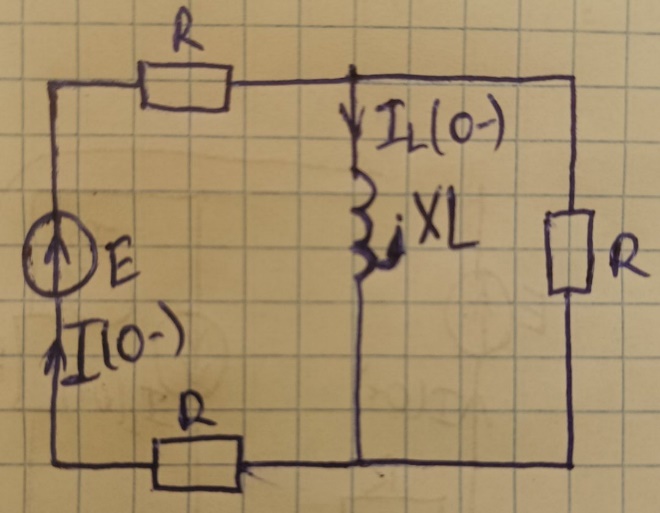
По правилу разброса найдём

2.1.2 ЗНУ (после коммутации )

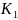2.1.3 ПС

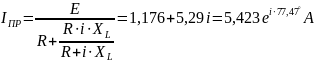
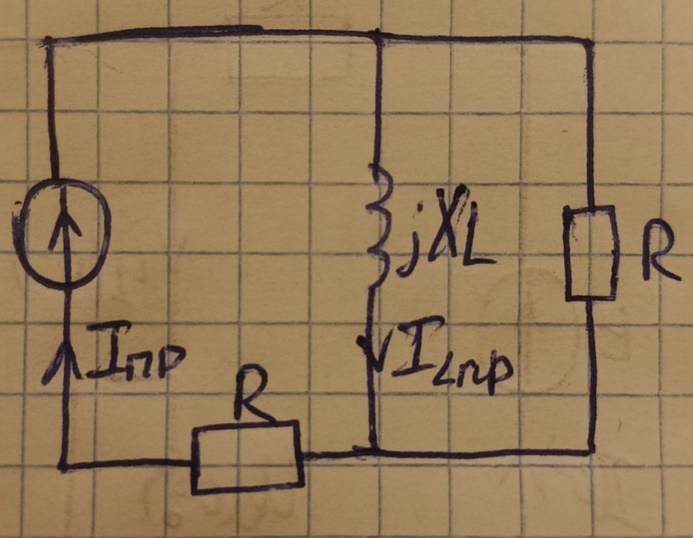
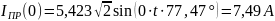
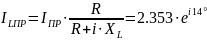
2.1.4 Определим корни характеристического уравнения

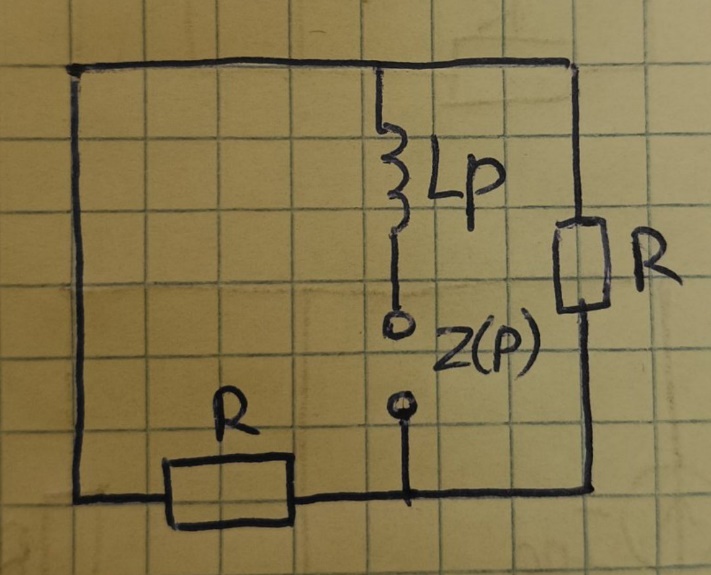
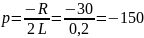
2.1.5 Определим постоянную интегрирования

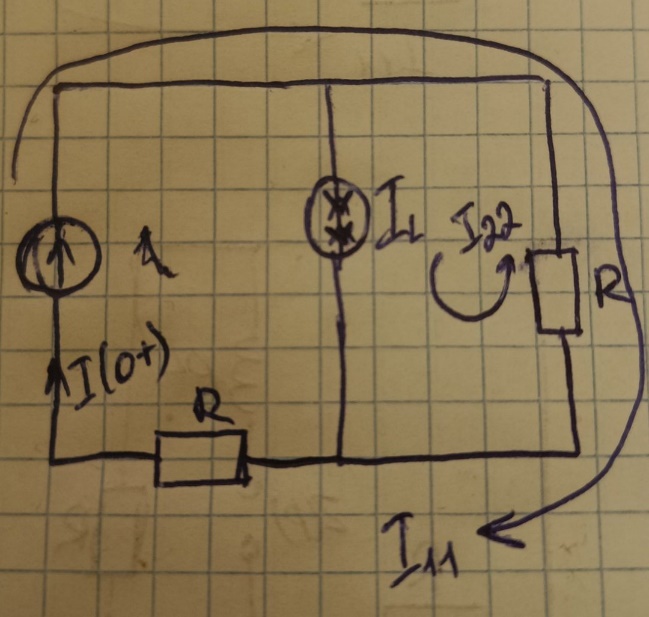
2.1.6 Результат

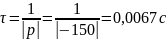
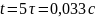
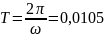
2.2 Используем комбинированный (операторно-классический) метод

2.2.1 ННУ

2.2.2 ПС возьмём из пункта 2.1.3

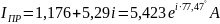
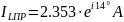
2.2.3 Определим начальные значения свободной составляющей тока

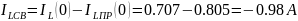
2.2.4 Операторная схема после коммутации свободной составляющей тока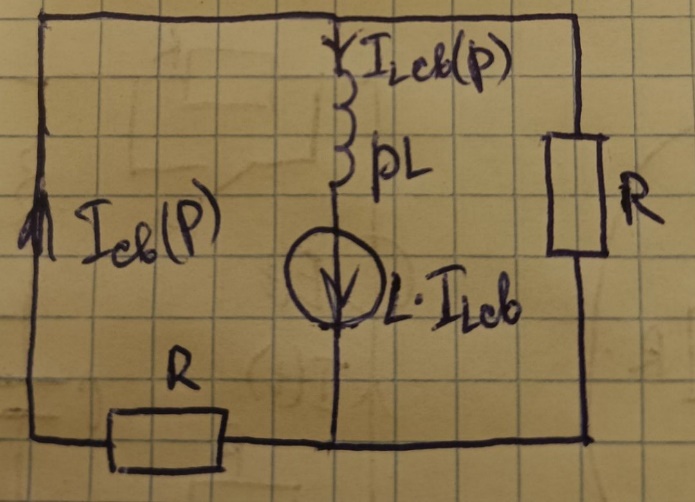

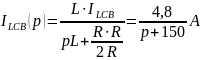
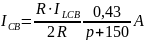
Пересмотреть

2.2.5 Используя теорему разложения и принцип наложения, получаем окончательный результат

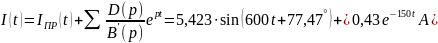
3. При импульсном источнике ЭДС

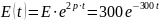
Ключ 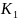сработал.

3.1 Находим переходную характеристику h(t) для I(t) операторным методом

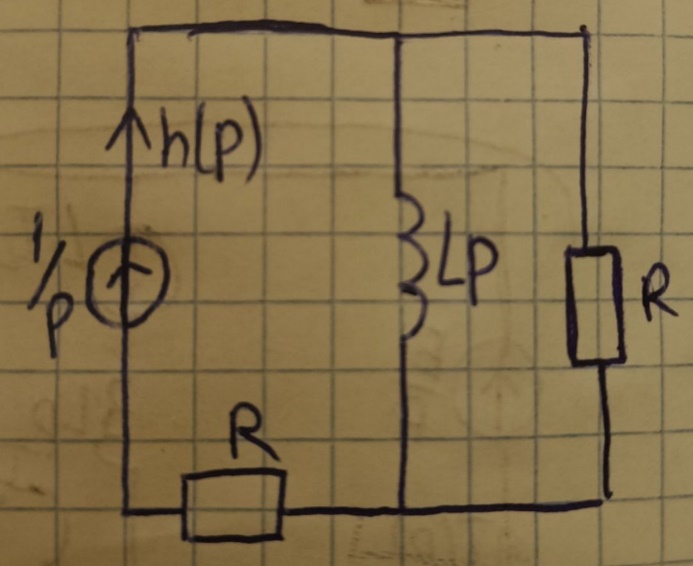
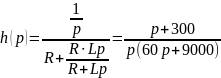
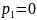
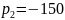
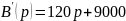
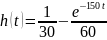
Проверка

а) t=0 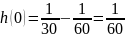L-разрыв

б) t=∞ 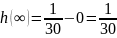L-закоротка

3.2 Рассчитаем интегралом Дюамеля

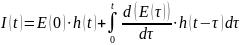
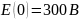
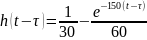
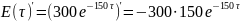
Произведём расчёт интеграла в Mathcad: Пересмотреть

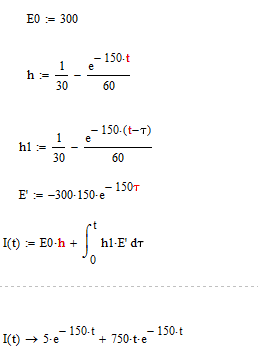
Получаем ответ:

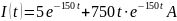
Построим график зависимости тока от времени:

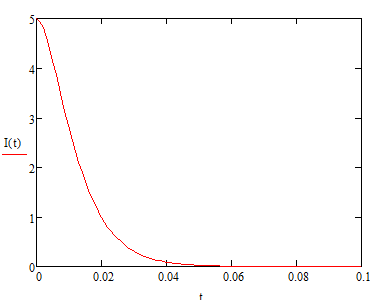
4. Цепь второго порядка.

При постоянном источнике после срабатывания ключа

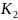
4.1

Схема, когда давно сработал

4.1.1 ННУ

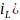
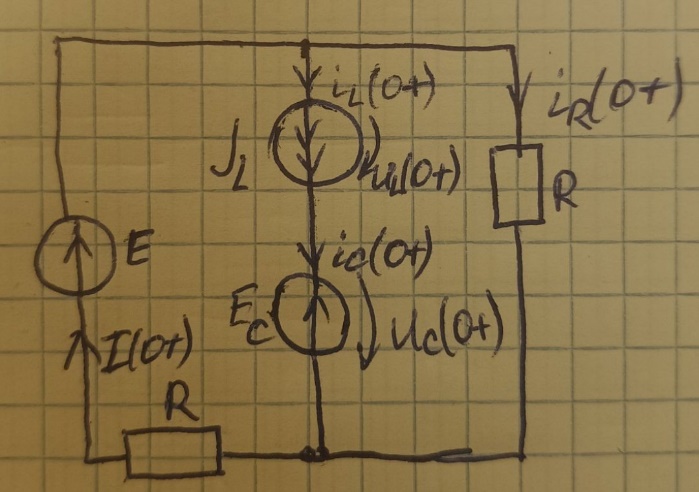4.1.2 ЗНУ

По законам коммутации

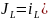
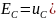
По законам Кирхгофа

Из уравнения 1

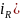
Подставим в уравнение 3

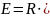
Получим

Из второго уравнения

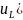
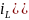
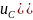
Найдём

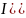
По законам Кирхгофа

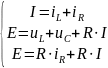
Из первого уравнения

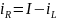
Из третьего уравнения

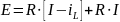
Отсюда

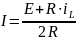
Тогда получим

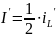
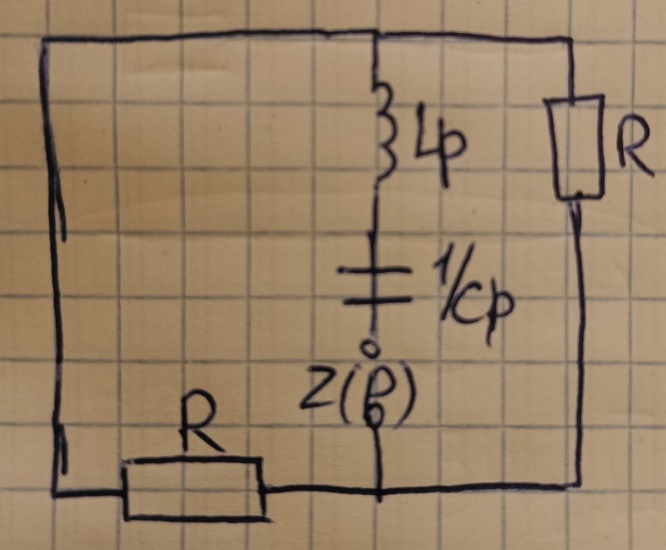
4.1.3 ПС

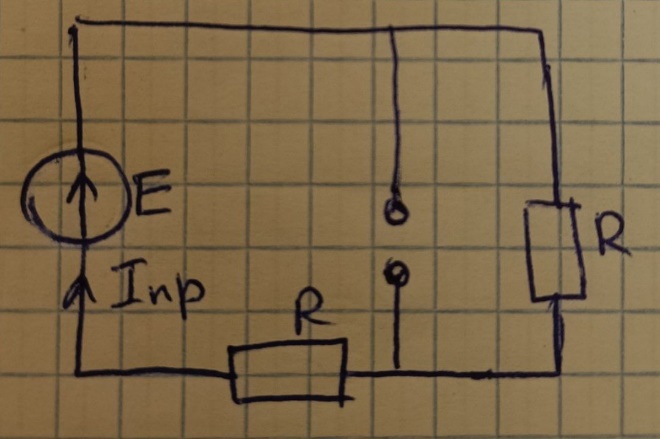
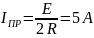
4.1.4 Определим корень характеристического уравнения

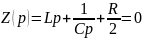
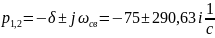
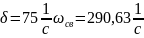
4.1.5 Определим постоянную интегрирования

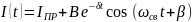
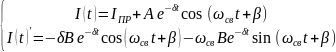
Или

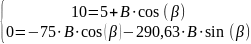
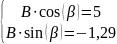
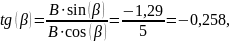
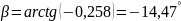
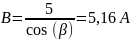
4.1.6 Окончательный результат

.

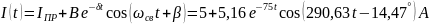Постоянная времени

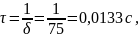
Длительность переходного процесса

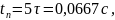
Период свободных колебаний

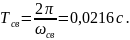
4.1.7 Построим график зависимости тока от времени на интервале

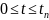
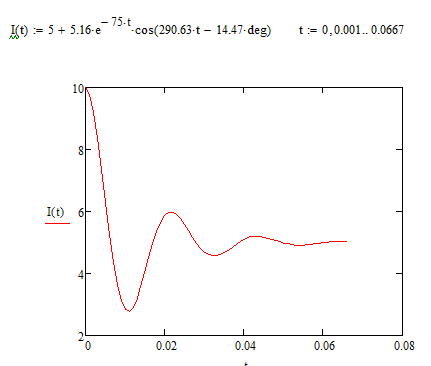
4.2 Используем операторный метод для определения i(t)

4.2.1 Из расчёта установившегося режима до коммутации находим ННУ(4.1.1)

4.2.2 В операторной схеме после коммутации используем метод наложения

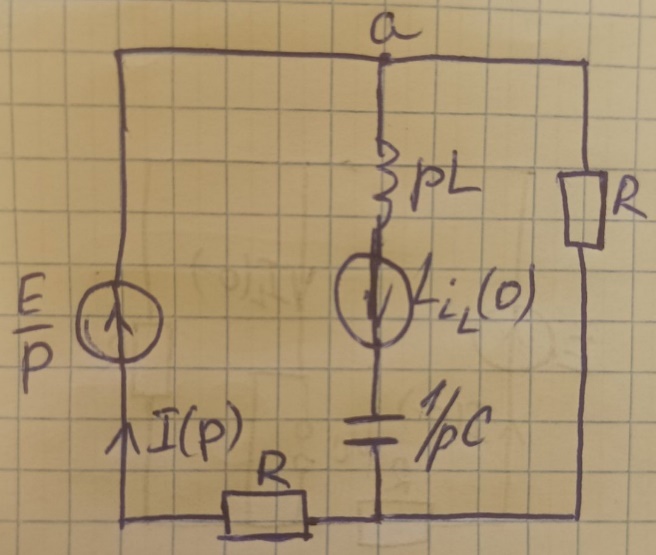
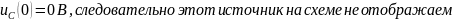
а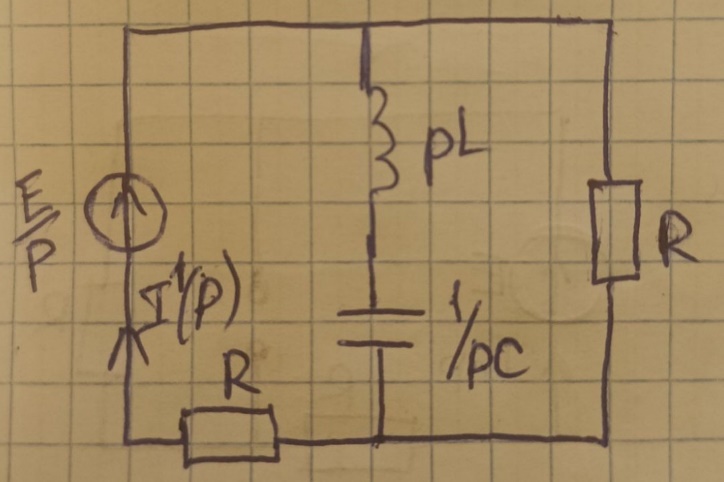 ) подсхема с источником ЭДС

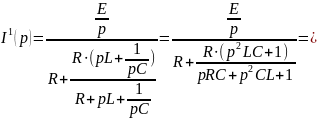
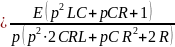
б ) подсхема с источником

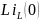
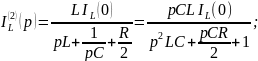
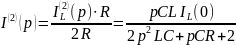
Операторное изображение искомого тока

.

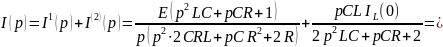
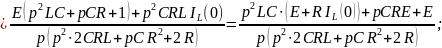
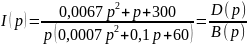
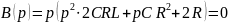
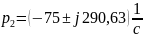
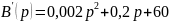
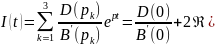
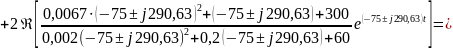
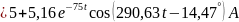4.3 Метод переменных состояний

4.3.1 ННУ

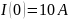
4.3.2 Составим уравнения состояния по законам Кирхгофа

Из первого уравнения

Из третьего уравнения

Отсюда

Из второго уравнения

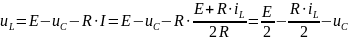
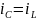
Тогда

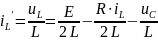
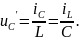
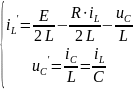
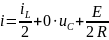
4.3.3 Решим методом Эйлера в MathCAD

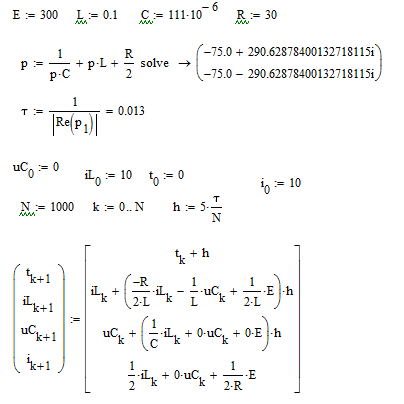
Построим график зависимости I(t)

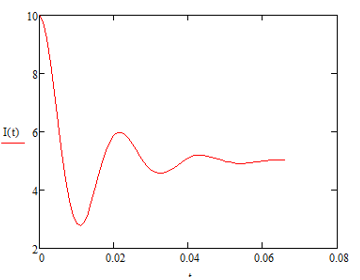
Вывод: все методы расчета показали возможность их применения для расчета переходных процессов в линейных электрических цепях.

Расчёты были произведены классическим(постоянный и гармонический источник), операторным(постоянный и переменный источник напряжения), комбинированным(импульсный источник напряжения) методами, интегралом Дюамеля(экспоненциальный источник напряжения), методом переменных состояний и методом Эйлера.

Результаты методов расчета цепей первого и второго порядка соответствуют друг другу.