§ 7. Магнитное поле постоянного тока

1. Закон Био –Савара-Лапласа. Магнитная индукцияполя, создаваемого элементом проводника с током

,

или

,

где μ_о— магнитная постоянная (μ_о=4π10^-7Гн/м), μ — магнитная проницаемость среды (для вакуума μ=l),- радиус-вектор.

2. Магнитная индукция 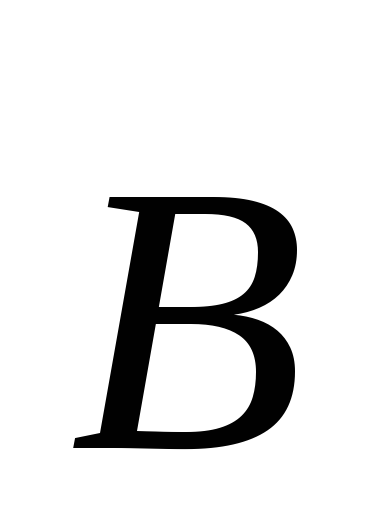связана с напряженностьюмагнит­ного поля соотношениемμ_о μ , или в вакуумеμ_о

3. Магнитная индукция в центре кругового проводника с током:

,

где R— радиус кривизны проводника.

4. Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:

,

где r— расстояние от оси проводника.

Магнитная индукция поля, создаваемого отрезком проводника на расстоянии rот него.

Обозначения ясны из рисунка. Вектор индукции перпендикулярен плоскости чертежа, направлен к нам и поэтому изображен точкой.

При симметричном расположении концов проводника относительно точки, в которой определяется

магнитная индукция, cosφ₂ = соsφ₁=cosφ и, следовательно,

.

5. Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси):

= μ_о μ I,

где n— число витков, приходящихся на единицу длины соленоида,I— сила тока в одном витке.

Магнитный момент рамки с током , где- единичная нормаль к плоскости рамки.

При наложении магнитных полей (в соответствии с принципом суперпозиции магнитных полей) магнитная индукция результирующего поля равна векторной (геометрической) сумме магнитных индукций, складываемых полей:

В частном случае наложения двух полей:

= ₁+_{2 ,}

а абсолютное значение вектора магнитной индукции:

,

где α — угол между векторами ₁ и .

6. Закон Ампера - сила, действующая на элемент тока,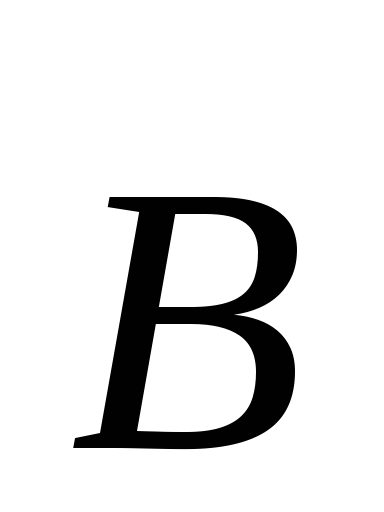- индукция магнитного поля в месте нахождения элемента тока.

7. Магнитное поле свободно движущегося заряда .

8. Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора индукции магнитного поля )

§8. Сила, действующая на заряд, движущийся в магнитном поле

Сила, действующая на зарядqдвижущийся со скоростьюв магнитном поле с индукцией, выражается формулой (сила Лоренца)

, где α — угол, образованный вектором скорости движения частицы и вектором индукции магнитного поля.

§ 9. Работа перемещения проводника с током в магнитном поле. Электромагнитная индукция. Индуктивность.

1. Работа перемещения замкнутого контура с током в магнитном поле определяется соотношением

где ΔФ — изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.

2. Основной закон электромагнитной индукции (закон Фарадея — Максвелла). Электродвижущая сила ε_iиндукции, возникающая в замкнутом контуре, пропорциональна скоростиизменения магнитного потока со временем:

где N — число витков контура, — потокосцепление; если все витки катушки пронизываются одним и тем же потоком, то=NФ.

3. Разность потенциалов Uна концах проводника длиной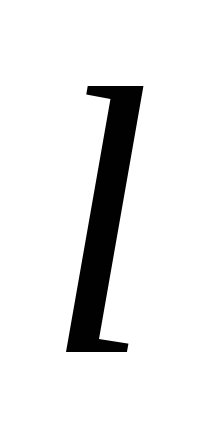, движущегося в однородном магнитном поле с постоянной скоростьюv, выражается формулой

U=Blv sinα,

где α— угол между направлением вектора скоростии вектора магнитной индукции.

4. Электродвижущая сила индукции ε_i, возникающая в рамке, содержащей N витков площадьюS, при вращении рамки с угловой скоростью( в однородном магнитном поле с индукциейопределяется уравнением

ε_i=BNSω sinωt,

где ωt— мгновенное значение угла между вектороми вектором нормали к плоскости рамки.

Электродвижущая сила самоиндукции ε_i, возникающая в зам­кнутом контуре при изменении силы тока в нем, пропорциональна скорости изменения силы тока:

,

где L- индуктивность (коэффициент самоиндукции) контура.

5. Потокосцепление ψ пропорционально силе тока I, протекающего по контуру,

=LI,

где L— индуктивность контура.

6. Индуктивность L соленоида (тороида) пропорциональна квадрату числа витков на единицу длины соленоида и объемуVсоленоида

L= μ_o μ n²V.

Магнитная проницаемость μсердечника соленоида (тороида) зависит от напряженности магнитного поля. Во всех случаях вычис­ления индуктивности соленоида (тороида) с сердечником по приведенной формуле для определения магнитной проницаемости следует пользоваться графиком зависимостиот , а затем формулой

.

7. Объемная плотность энергии магнитного поля

8. Намагниченность

9. Связь между векторами и ,

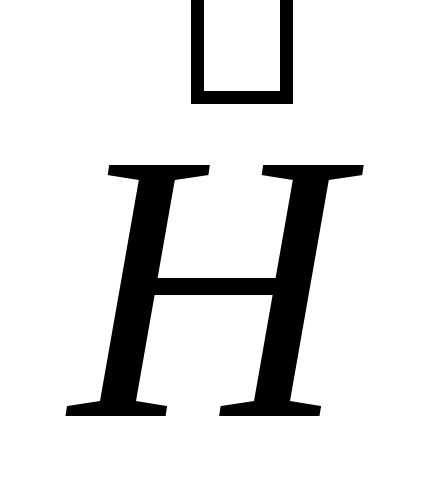
10. Теорема о циркуляции вектора

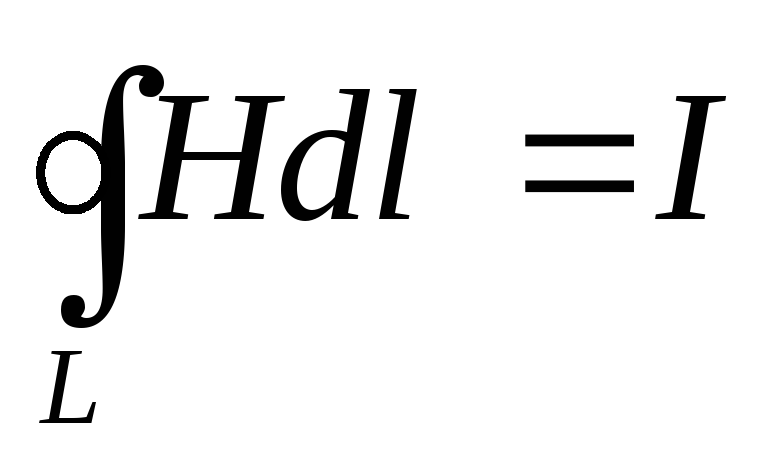
11. Мгновенное значение силы тока Iв цепи, обладающей сопротивлениемrи индуктивностьюL:

а) после замыкания цепи:

где ε— э. д. с. источника тока,t — время, прошедшее после замыка­ния цепи;

б) после размыкания цепи:

где I_о— значение силы тока в цепи приt=0,t— время, прошедшее с момента размыкания цепи.