Основы_акустики_Гринченко_Вовк

Рис. 8.6. Зависимости σ(ψ)/πа при разных значениях волнового радиуса ци- линдра: а — жесткий цилиндр, б — мягкий цилиндр

На рис. 8.6 показано позиционное сечение рассеяния при соответ- ствующих значениях волнового радиуса цилиндра ka. Сначала рас- смотрим рассеяние звука цилиндром на низких частотах, т.е. при ka < 1. В наших расчетах это соответствует ka ≤ 0,3. Следует обратить внимание, с одной стороны, на характер кривой, а с другой — на ве- личину позиционного сечения рассеяния. Как видим, в случае мяг- кого цилиндра (рис. 8.6, б, ka ≤ 0,3) диаграмма рассеяния подобна круговой диаграмме, что характерно для монопольного рассеяния, а для жесткого цилиндра (рис. 8.6, а, ka ≤ 0,3) — подобна кардиоидной диаграмме, которая образуется как суперпозиция монопольного и дипольного рассеяний. Монопольное рассеяние малым препятствием, как уже отмечалось, обусловлено только различием в сжимаемостях препятствия и среды. Для жесткого цилиндра сжимаемость равна ну- лю. Дипольное рассеяние связано с таким препятствием, которое от- личается от среды только плотностью. Этот результат можно проком- ментировать следующими физическими соображениями. В звуковой волне происходят процессы сжатия и смещение частиц среды. Малое препятствие в звуковом поле, по сути, малая частица, в виде жестко- го цилиндра изменяет характер сжатия и смещения частиц среды вблизи цилиндра. Это обуславливает возникновение рассеянной вол- ны, такой, что на поверхности цилиндра должны выполняться гра- ничные условия: радиальная скорость равна нулю. Таким образом, изменение характера сжатия приводит к монопольному рассеянию, а изменение характера движения частиц среды приводит к дипольно- му рассеянию, причем вклад обоих типов рассеяния оказывается примерно одинаковым, в чем несложно убедиться.

Обратимся к формуле (8.44) для давления в рассеянной волне же- стким цилиндром и определим асимптотическое поведение коэффициентов Bn (формула (8.33) при ka → 0). Используя соотношение (8.40), получаем

511

Коэффициенты Bn при n > 1 имеют порядок малости высший, чем (ka)2 (убедитесь в этом самостоятельно). Как следствие, нормирован- ную амплитуду давления рассеянной волны от жесткого цилиндра

Как видим, первое слагаемое в (8.51) определяет монопольное рассея- ние, а второе слагаемое - дипольное рассеяние. Запишем соответст- вующую нормированную интенсивность

Рассмотрим мягкий цилиндр малых волновых размеров. Здесь асимптотика коэффициентов Bn (формула (8.34)) при ka → 0 имеет

коэффициенты Bn при n > 0 пропорциональны (ka)2n и, следовательно, при (ka) << 1 будут значительно меньшими, чем коэффициенты В0 (убедитесь в этом).

Таким образом, оставляя первый член ряда (8.44), можно записать следующее выражение для нормированной амплитуды давления рас-

которое не зависит от угла ψ и представляет собой рассеянием моно- польного типа. Как следствие, дипольное рассеяние для мягкого ци- линдра при (ka) << 1 значительно меньше, чем рассеяние монопольно- го типа.

Обратим внимание на числовые значения σ(ψ)/πа при ka < 1. Как видно из графиков (рис. 8.6, ka ≤ 0,3), в случае мягкого цилиндра

512

значения σ (ψ)/πа значительно превышают соответствующие значе- ния для жесткого цилиндра. Согласно формулам (8.51) и (8.54), кото- рые справедливы для (ka) << 1, величина σs/πа для жесткого цилинд- ра стремится к нулю при ka → 0, а в случае мягкого цилиндра — σ(ψ)/πа → ∞. Природа бесконечности уже обсуждалась при анализе колебательной скорости на поверхности мягкого цилиндра, и понят- но, что в случае цилиндра конечной длины этой бесконечности не бу- дет. Итак, приходим к выводу: если в случае жесткого цилиндра рас- сеянное поле уменьшается до нуля при ka = 2πa/λ → 0, то в случае мягкого цилиндра рассеянное поле будет иметь конечное значение при любом малом размере волнового радиуса ka.

При увеличении волнового радиуса цилиндра (ka) вид диаграмм постепенно усложняется (рис. 8.6). Появляется характерная особен- ность высоких частот: рассеяние вперед, в направлении падающей волны, которое больше, чем рассеяние в противоположном направле- нии. Формируется так называемый теневой лепесток характеристи- ки. С ростом ka диаграмма фактически разделяется на две части: первая из них определяет рассеяние в сторону падающей волны, а вторая формирует теневой лепесток.

Картина рассеяния звука цилиндром с ростом величины ka в об- щих чертах имеет такой вид. Одна часть энергии рассеивается в сто- рону падающей волны. При больших ka угол отражения звука от по- верхности цилиндра соответствует законам геометрической акусти- ки. Другая часть энергии создает теневую волну. Фаза этой волны противоположна фазе падающей волны, а амплитуды обеих волн ока- зываются одинаковыми. В поле за цилиндром, определенном супер- позицией этих волн, создается зона тени. Это действительно так, ведь согласно постановке задачи (см. формулу (8.22)) падающая плоская волна существует в пространстве всюду и потому рассеянное поле должно иметь именно такие свойства.

При дальнейшем увеличении волнового радиуса ka разделение рассеянной волны на отраженную и теневую оказывается все более сильным. В предельном случае, когда ka становится очень большим, теневой лепесток имеет малый угол раскрыва, стремящийся к нулю. Фактически имеем случай рассеяния звука на препятствии большого волнового размера, в этом случае взаимодействие звука с препятст- вием хорошо описывается на основе лучевых представлений (рис. 8.2). Поэтому понятно, что при ka >> 1 даже при малом отклонении от максимума теневого лепестка мы попадаем в зону “освещенную” па- дающей волной. Неограниченный рост максимума теневого лепестка не должно удивлять. Дело в том, что, с одной стороны, существует падающая плоская волна, у которой амплитуда не зависит от рас- стояния, а с другой — рассеянная цилиндрическая волна, у которой

513

Is 1/r. С учетом того, что точка наблюдения принадлежит дальнему полю (kr → ∞), становится понятным существование этой особенно- сти.

Выше шла речь о теневом лепестке при росте волнового размера ka. Рассмотрим теперь, какой характер имеет рассеяние звука в на- правлении, противоположном направлению падающей волны, с уве- личением ka. Как видим (рис. 8.6), в окрестности угла ψ = 180° с рос- том ka кривые, осциллируя, скапливаются вокруг единицы. Физиче- ски этот результат иллюстрирует понятную ситуацию: от идеального препятствия большого волнового размера коэффициент отражения в противоположном направлении равен единице.

Теперь определим полную мощность рассеянной волны, которая приходится на единицу длины цилиндра. Для этого проинтегрируем функцию (8.47) по поверхности цилиндра радиуса r и единичной вы- соты:

Тогда полное сечение рассеяния цилиндра по определению (8.7) равно

Полное сечение рассеяния цилиндра может быть как больше, так и меньше, чем геометрическое сечение 2а (определяем на единицу дли- ны образующей цилиндра). Чтобы в этом убедиться, проведем анализ ситуации в случае, когда ka >> 1, и когда ka << 1.

Для волн, которые имеют большую длину волны (ka << 1), в случае жесткого цилиндра, используя (8.50), в ряде (8.56) можно удержать только два первых члена:

Таким образом, на низких частотах согласно (8.52) и (8.57) интенсив- ность рассеянной волны зависит от угла ψ по закону (1 – 2 сosψ)2, а

514

полное сечение рассеяния жесткого цилиндра значительно меньше, чем его диаметр.

Для мягкого цилиндра с малым волновым радиусом (ka << 1) си- туация иная. Действительно, согласно оценке (8.53) в этом случае в ряде (8.56) достаточно удерживать только первый член:

(имеем предел lim (ka ln2 ka) = 0 ). Итак, рассеянная волна для малого ka →0

мягкого цилиндра (ka << 1) равномерно распределена по всем направ- лениями, и полное сечение рассеяния значительно больше геометри- ческого сечения цилиндра.

Анализ асимптотического поведения коэффициентов Bn в формуле (8.56) при ka >> 1 показывает [31, с. 295—296], что на высоких час- тотах сечение рассеяния как для мягкого, так и для жесткого цилин- дров, равно удвоенному геометрическому сечению, т.е. σ = 4а. Полу- ченный результат соответствует общему анализу рассеяния плоской волны на выпуклых телах большого волнового размера (см. формулу

(8.9)).

Рис. 8.7. Зависимость полного сечения рассеяния идеального цилиндра и идеальной сферы от волнового радиуса ka:

1 — жесткий цилиндр; 2 — мягкий цилиндр; 3 — жесткая сфера; 4 — мягкая сфера

515

На рис. 8.7 приведенные численные расчеты величины σs /2a по точной формуле (8.56). Как видим, если ka >> 1, то для обоих цилинд- ров величина σs /2a → 2; если ka << 1, то величина σs /2a стремится к нулю для жесткого цилиндра и возрастает в случае мягкого цилиндра. Еще раз отметим, что это неограниченное увеличение величины σs при ka → 0 связано с бесконечной длиной цилиндра. Для цилиндра конеч- ной длины, такой нефизический результат, отсутствует.

8.7. Рассеяние плоской волны на идеальной сфере

Внесем в однородную среду, в которой распространяется плоская волна, тело сферической формы. Как следствие этого появля- ется рассеянная волна. Полное поле, образованное суперпозицией плоской и рассеянной волн, должно удовлетворять граничным усло- виям на поверхности сферы. Как мы уже знаем, задачу рассеяния звука можно свести к задаче излучения, которую сформулируем сле- дующим образом: рассеянное поле создается вследствие некоторого распределения давления (в случае жесткой сферы) или нормальной скорости (мягкая сфера) на поверхности сферы. Это распределение является таким, что вместе с полем падающей плоской волны оно должно удовлетворять соответствующим граничным условиям.

Рис. 8.8. Пример падающей плоской волны на сферу

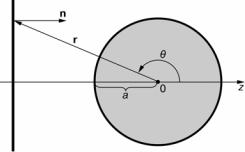
Задачу следует решать в сферических координатах (r, θ, ψ). Не ограничивая общности решения, можно считать, что плоская волна р0 распространяется вдоль положительного направления оси Oz (рис. 8.8). В такой ситуации поле рассеянной волны не зависит от уг- ла ψ, что позволяет определить амплитуду давления рассеянного поля в виде (см. формулу (7.195)):

Давление падающей волны (рис. 8.8) запишем в виде

516

Рис. 8.9. Диаграммы распределения (справа), графики (слева) для нормиро- ванной амплитуды давления вблизи жесткой сферы, а/λ = 0,9:

1 — θ = 180°; 2 — θ = 0°

Используя эти формулы, можно, как это было сделано в случае с цилиндром, решать разные задачи, связанные с рассеянием звука на сфере. Например, на рис. 8.9 представлено распределение нормиро- ванной (относительно амплитуды падающей плоской волны) амплиту- ды давления вокруг идеально жесткой сферы. Интересно отметить, что если для цилиндра (рис. 8.5, а) в точке, противоположной направ- лению падения волны (ψ = 0) наблюдаем образование теневой зоны, то в аналогичной ситуации для сферы (рис. 8.9, θ = 0) имеем давле- ние, близкое по значению к давлению в падающей волне, т.е. тень “освещается”. Это так называемая пятно Пуассона . Такая особен- ность объясняется тем, что в области геометрической тени на полу- прямой θ = 0 сходятся, имея одинаковую фазу, дифракционные вол- ны от всех точек экватора сферы, а в случае цилиндра — только от двух точек его профиля. Понятно, что в области геометрической тени для углов θ ≠ 0 такая синфазность нарушается. Наличие пятна Пуас- сона будет наблюдаться при рассеянии волны и на других телах, на- пример, при осевом падении волны на диск.

Подробнее рассмотрим такую важную характеристику, как полное сечение рассеяния. Рекомендуем читателю самостоятельно (в полной аналогии с цилиндром) провести последовательность выкладок. Сна- чала, имея давление рассеянной волны (8.71), следует записать вы-

Пуассон (Poisson) Симеон Дени (1781—1840) — французский механик, физик и математик.

519

ражение для колебательной скорости υrs. Далее, используя асимптоти- ку сферической функции Ханкеля при kr → ∞ (см. формулу (8.41)):

нужно записать выражения для давления ps и скорости υrs в дальнем поле при kr → ∞. Далее запишите выражение для интенсивности рас- сеянного поля на большом волновом расстоянии от сферы:

Используя свойство ортогональности полиномов Лежандра (8.63), полу- чаем окончательный результат:

Очень интересным является случай сферы малого волнового радиу- са (ka << 1). Выполним преобразования в формуле (8.76) на основе