Базовые средства матпакета Scilab

xopt – вектор аргументов, обеспечивших оптимальное значение функции;

gopt – градиент целевой функции (или производной в случае одномерной оптимизации) в точке xopt;

work – рабочий массив перезапуска для Квази-Ньютоновских методов. iters – скаляр, число итераций, которое отображается при iprint=2. evals – скаляр, число вычислений функции cost, которое отображается

при iprint=2.

– скаляр, индикатор завершения, может иметь следующие

err=1 – норма вычисленного градиента ниже допустимого;

err=2 – на последней итерации f уменьшается;

err=3 – оптимизация останавливается из-за слишком малых

изменений для X;

err=4 – остановка: максимальное количество обращений к f;

err=5 – остановка: максимальное количество итераций;

err=6 – остановка: слишком маленькие изменения в

направлении градиента;

err=7 – остановка: во время расчета направления спуска;

err=8 – остановка: во время расчета оценки матрицы Гессе;

err=9 – окончание оптимизации, успешное завершение;

err=10 – успешное окончание оптимизации (линейный поиск

не выполняется).

Каждый алгоритм, реализованный в optim, имеет свои собственные критерии завершения, которые могут использовать параметры, полученные от пользователя, такие как: nap, iter, epsg, epsf и epsx.

Рассмотрим пример использования решателя optim для случая решения задачи оптимизации одномерной функции f(x)=x4+3x3-13x2-6x+26, имеющей на отрезке [-4;-2] единственный минимум (исследование которой приведено выше на рис. 2.7.1-2 и 2.7.1-3), выбрав в качестве начальной точки х0=-3 (рис. 2.7.3-1). В нашем случае используется достаточно простой формат функции optim – передается имя вспомогательной функции (costf) и начальное значение аргумента (х0), а в качестве выходных параметров выступают координаты точки минимума функции f(х).

271

-->// Нахождение координат точки минимума с использованием решателяoptim

--> -->exec('РИС2731.sce'); -->x0 = -3;

--> // Вычисление координат точки минимума

--> [fmin, xmin] = optim(costf, x0); // Обращение к функции optim --> disp([fmin, xmin])

-95.089413 -3.8407084

Рис. 2.7.3-1. Нахождение координат точки минимума функции f(x)с использованием решателя optim

В примере, приведенном на рис. 2.7.3-1 для вычисления производной используется функция numderivative, что позволяет устранить проблему получения аналитических выражений производных в случае сложного выражения целевой функции. Однако использовать эту функцию совсем необязательно. Так, например, на рис. 2.7.3-2 приведен сценарий, в котором для вычисления значений производной используется аналитическое выражение.

Рис. 2.7.3-2. Вычисление производной с использованием ее математического выражения

272

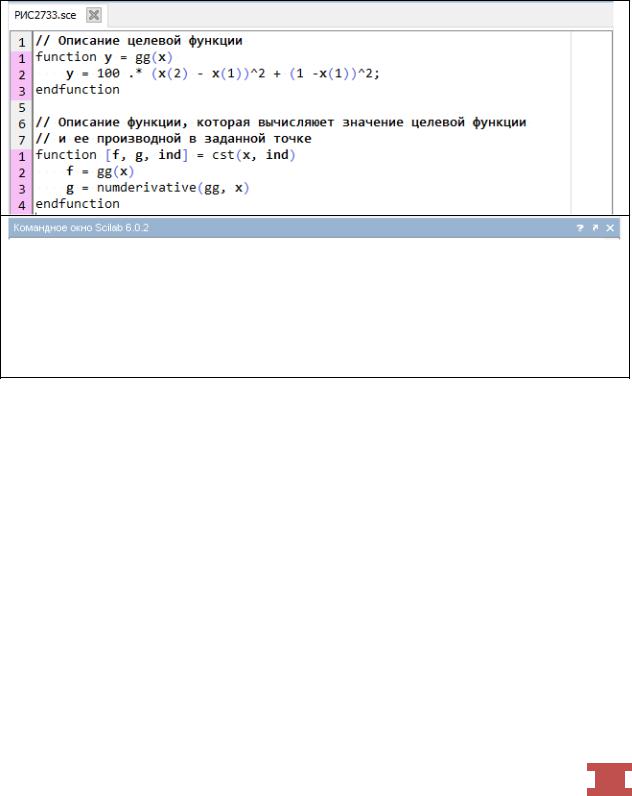
В следующем примере (рис.2.7.3-3) определим координаты точки минимума и значение многомерной функции Розенброка:

f(x1,x2)=100(x2-x12)2+(1-x1)2,

с использованием того же упрощенного формата функции optim. Ранее (рис.2.7.1-4) в качестве начального приближения уже был выбран вектор начальных значений [0,0].

--> // Нахождение минимума многомерной функции f(x1,x2)

-->

-->exec('РИС2733.sce', 0);

-->x0 = [0; 0]; // Начальныезначения

Рис. 2.7.3-3. Использование функции optim для нахождения координат точки минимума многомерной функции f(x1,x2)

Отметим, что в описанных выше примерах были использованы самые простые форматы функции optim. Однако в процессе вычислений часто представляет интерес: сколько итераций потребовалось для нахождения минимума той или иной функции, причину прекращения итерационного процесса и многие другие моменты, которые могут быть выявлены при использовании других, описанных выше, форматов этой функции.

Именно поэтому пользователю, решающему серьезные задачи оптимизации крайне важно рассмотреть и проанализировать результаты выполнения следующего примера (рис. 2.7.3.4), показывающего возможности использования различных (необязательных) параметров функции optim.

273

--> // Загрузка сценария РИС2734

--> // и обращение к решателю optim с дополнительными параметрами

--> //

xopt=0.5 1. 3.;fopt=0.625; gopt=-0.5 -1.5559108 -0.7779554

xopt=0.5 1. 2.2220446 fopt=1.6380365 gopt=-0.5 -1.8308232 -0.9154116 xopt=0.5 1. 2.0845884 fopt=2.2199459

***** enters -qn code- (without bound cstr)

dimension=3, epsq=0.2220446049250313E-15, verbosity level: iprint=3

274

***** leaves -qn code-, gradient norm= 0.0000000000000000E+00 optim: Норма проектируемого градиента ниже, чем 0.

xopt = 1. 2. 3. fopt = 0.

Рис. 2.7.3-4. Применение дополнительных параметров при использовании функции optim

Решатель fminsearch

Решатель fminsearch – вычисляет безусловный минимум функции по алгоритму Нелдера-Мида и имеет следующие форматы [13]:

X=fminsearch(costf,х0) X=fminsearch(costf,х0,options) [X,fval]=fminsearch(costf,х0,options) [X,fval,exitflag]=fminsearch(costf,х0,options)

[X,fval,exitflag,output]=fminsearch(costf,х0,options)

Этот решатель является алгоритмом прямого поиска, не использующим производную целевой функции, а основан на обновлении симплекса, который является набором k>=n+1 вершин, где каждая вершина связана с одной точкой и одним значением функции. Алгоритм создан на базе neldermead компонент [13].

Рассмотрим подробнее назначение параметров:

Входные параметры:

сostf – внешняя функция, которая возвращает значение целевой функции и имеет следующий заголовок

где X– текущая точка;

f – значение целевой функции;

X0 – матрица начальных значений;

options – структура данных, содержащая настраиваемые параметры алгоритма оптимизации, значения которых и определяют

конфигурацию алгоритма fminsearch, причем fminsearch чувствительна к следующим опциям:

options.MaxIter – максимальное количество итераций, значение по умолчанию – 200*n, где n- количество переменных;

276

options.MaxFunEvals – максимальное количество оценок функции затрат, значение по умолчанию – 200*n, где n – количество переменных;

options.TolFun – абсолютный допуск по значению функции, значение которого по умолчанию – 1.e-4;

options.TolX – абсолютный допуск на размер симплекса, значение по умолчанию – 1.e-4;

options.Display – подробный уровень, для которого возможны значения: "notify","iter","final" или "off", значение по умолчанию –

"notify";

options.OutputFcn – выходная функция или список выходных функций;

options.PlotFcns – функция печати или список функций печати.

Выходные параметры:

X – значение аргумента, обеспечившее минимальное значение функции;

fval– минимальное значение функции.

– флаг, связанный со статусом выполнения алгоритма:

– максимальное количество итераций достигнуто;

0– максимальное число оценок функций достигнуто;

1– допуск на размер симплекса и его изменения уже достигнут: алгоритм не имеет сходимости;

output.funcCount – количество оценок функции; output.iterations – количество итераций;

output.message – строка, содержащая сообщение о завершении.

Критерии прекращения процесса оптимизации используют следующие переменные:

ssize – текущий размер симплекса;

shiftfv – абсолютное значение разности значения функции между самой высокой и самой низкой вершиной.

Процесс итерации останавливается, если выполняются следующие

условия: ssize<options.TolFun&shiftfv<options.TolFun.

Алгоритм, заложенный в fminsearch использует специальный начальный симплекс, который вычисляется эвристически в зависимости от начального предположения (подробнее см. в документации о optimsimplex

[x]) .

В следующих примерах для вычисления минимума функции Розенброка воспользуемся решателем fminsearch, описав предварительно

277

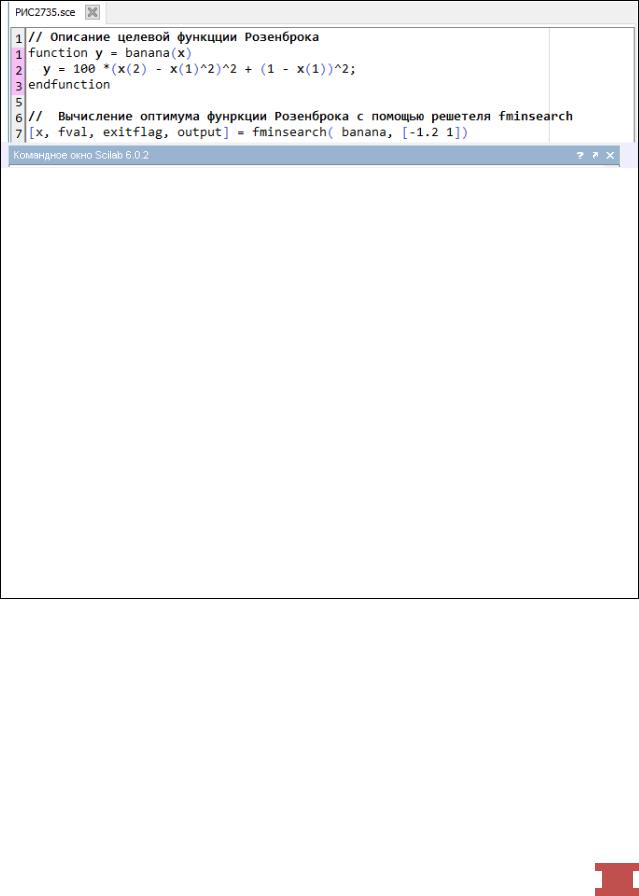
функцию под именем banana, и задав начальные значения поиска [-1.2 1.0]. В данном случае для поиска минимума потребовалось выполнение 85 итераций и 159 обращений к функции оценки (рис. 2.7.3-5).

--> // Загрузка сценария РИС2735

--> // и вычисление минимума с использованием решателя fminsearch

-->

--> exec('РИС2735.sce', 0)

[output.Output, output.funcCount, output.iterations, output.message] exitflag =

1. fval =

0.00000000081776611 x =

1.0000220217835567 1.0000422197517711

--> mprintf('algorithm = %c\nfuncCount = %4d\niterations = %3d',… output.algorithm, output.funcCount, output.iterations);

algorithm = Nelder-Mead simplex direct search funcCount = 159

iterations = 85 --> output.message ans =

!Optimization terminated:

!

! the current x satisfies the termination criteria using OPTIONS.TolX of 0.0001 ! and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 0.0001 !

Рис. 2.7.3-5 Вычисление минимума функции Розенброка с использованием решателя fminsearch

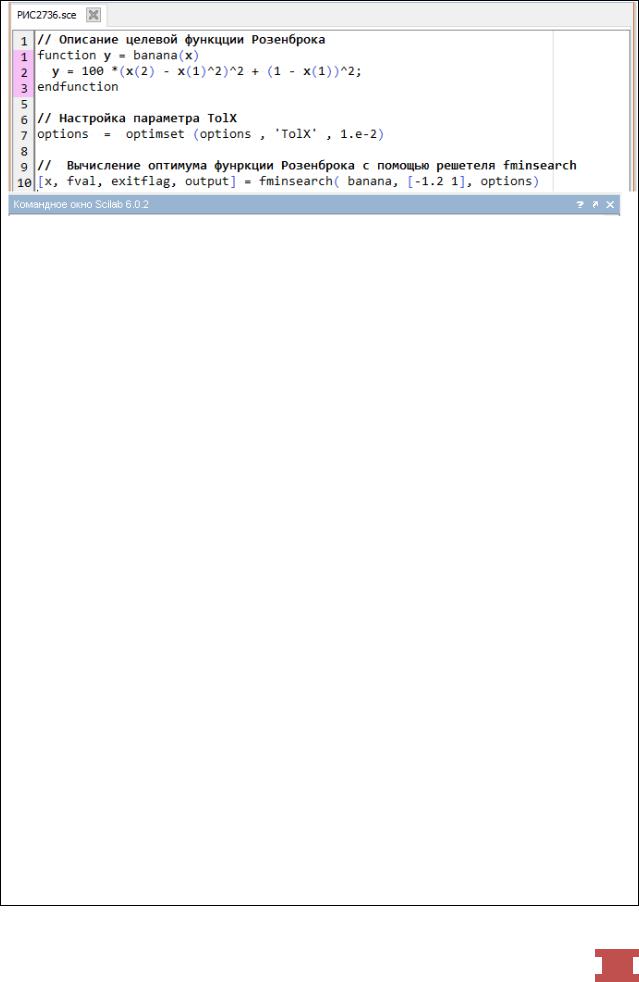
Далее рассмотрим пример вычисление минимума функции Розенброка решателем fminsearch с настраиваемыми опциями. Настроим абсолютный допустимый размер симплекса до большего значения, так чтобы алгоритм выполнял меньшее количество итераций. Поскольку по умолчанию значение tolX=1.e-4, заменим его в optimset на большее значение, например, 1.e-2. В данном случае потребовалось 70итераций и 130обращений к функции оценки (рис. 2.7.3-6).

278

-->// Загрузка сценария РИС2735, настройка некоторых опций -->// и вычисление минимума с использованием решателяfminsearch

--> exec('РИС2736.sce', 0)

options =

Display: [0x0 constant] FunValCheck: [0x0 constant] MaxFunEvals: [0x0 constant] MaxIter: [0x0 constant] OutputFcn: [0x0 constant] PlotFcns: [0x0 constant] TolFun: [0x0 constant] TolX: [1x1 constant]

output =

algorithm: [1x1 string] funcCount: [1x1 constant] iterations: [1x1 constant] message: [3x1 string]

exitflag = 1.

fval = 0.0000085

x =

1.001016 1.0017605 -->

--> mprintf('algorithm = %c\nfuncCount = %4d\niterations = %3d',… output.algorithm, output.funcCount, output.iterations);

algorithm = Nelder-Mead simplex direct search funcCount = 130

iterations = 70 -->

--> output.message ans =

!Optimization terminated:

!

!the current x satisfies the termination criteria using OPTIONS.TolX of 0.01

!and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 0.0001

Рис. 2.7.3-6. Вычисление минимума функции Розенброка решателем fminsearch с настраиваемыми опциями

279

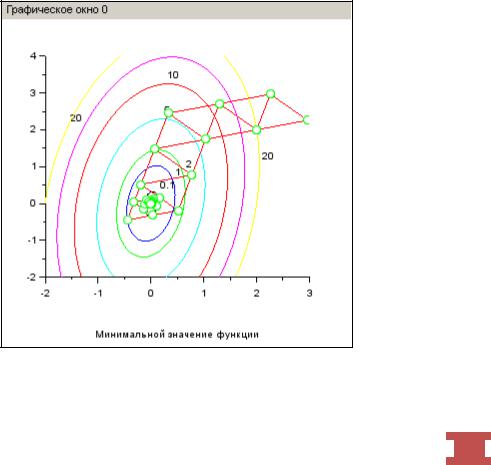
Решатель nmplot

Кроме описанных выше решателей optim и fminsearch, в Scilab представляет интерес решатель nmplot [13], который использует алгоритмы оптимизации прямого поиска, при этом всю информацию о процессе оптимизации на каждой итерации можно отобразить на экране или сохранить в файлах для ее последующего анализа.

Решатель nmplot включает несколько методов оптимизации прямого поиска, основанных на симплексном методе. Он является модификацией компонента neldermead, с выводом результатов, и позволяет хранить историю значений данных в процессе итераций.

Этими данные могут быть:

значения координат симплекса;

значения функции, усредненные по вершинам;

минимальные значения функции в симплексе;

размеры симплекса.

Во время процесса оптимизации эти данные хранятся в нескольких файлах.

На рис. 2.7.3-7 приведен пример только графической траектории поиска минимума функции с использованием решателя nmplot. Подробноэтотпримериспользования решателя nmplot рассмотрен в [13]. Из которого следует, что выбор направления спуска определяется симплексом.

Рис. 2.7.3-7 Траектория спуска при поиске минимума с использованием решателя nmplot

280