5. Вероятность ошибки и вероятность правильного

принятия решения

Определим вероятность ошибки  и вероятность правильного обнаружения D = 1 -  как функция порога с^* . Как известно, ошибка первого рода возникает тогда, когда принимается решение о наличии сигнала s(t) в принятой реализации в то время, как _{сигнал отсутствует. Вероятность этого события равна}

_{. (5.1)}

_{Для упрощения расчетов произведем нормирование случайной величины V , сдвинув V на величину условного математического ожидания при отсутствии сигнала M[V / s=0] и пронормировав полученное выражение относительно условного среднеквадратического отклонения  v0 при отсутствии сигнала}.

Сдвиг и нормировка производится как левой, так и правой частей неравенства (5.1). В результате преобразований формула (5.1) примет вид

(5.2)

где

, . (5.3)

Вероятность правильного обнаружения D = 1 -  как функция порога с^* есть вероятность превышения случайной величиной V порога с ^*, но при наличии сигнала в принятой реализации:

.

Точно также, как и в предыдущем случае , производится смещение случайной величины V на величину условного математического ожидания _{M( V / s  0 ) и нормировка ее относительно условного среднеквадратического отклонения Z, равного  v1}, но при наличии сигнала. В результате получим вероятность правильного обнаружения

(5.4)

где

, . _(5.5)

В интегральной форме вероятность ошибки  и вероятность правильного решения D = 1- имеют вид

, ( 5.10 )

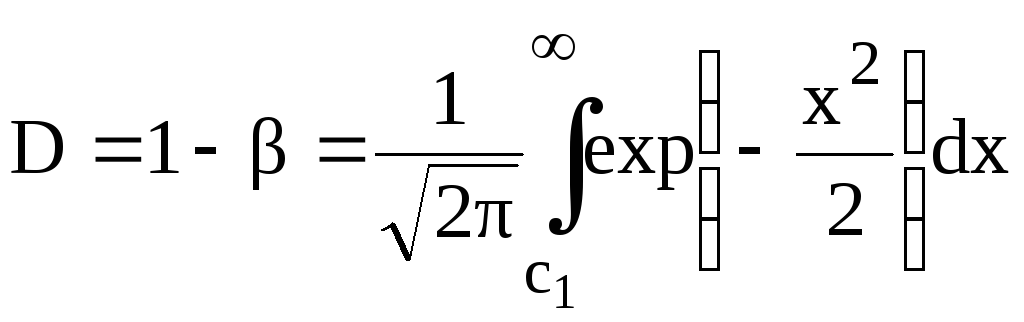, (5.11 )

где с ₀ и с ₁ вычисляются при помощи формул (4.18), (4.19), (4.24), (4.25), (4.29), (5.3), (5.5).

Формулы (5.10) и (5.11) позволяют построить рабочую характеристику приемника при использовании непрерывных наблюдений на интервале (0, ) .

6. Методика эксперимента

1. Для того, чтобы снять рабочую характеристику, необходимо измерить вероятность правильного обнаружения D=1- и вероятность ошибки первого рода . Эти вероятности измеряются методом статистических испытаний. Для измерения D=1- в течение времени Тн периодически воспроизводится передача “1” по каналу связи при заданном отношении сигнал/шум и фиксированном значении порога. (Переключатель П₁ в положении “Сигн.+Шум”, а переключатель П₂ в положениях “Е₁“, “Е₂ “, “Е₃ “).

В качестве оценки вероятности правильного обнаружения берется отношение числа импульсов на выходе приемника N_i к общему числу сигналов N^*, поступивших на вход приемника за время измерения Тн, т.е. D^*= N_i / N^* .

Для измерения  в течение времени Тн периодически воспроизводится передача “0” по каналу связи с определенным уровнем шума. (Переключатель П₁ в положении “Сигн.+Шум”, а переключатель П₂ в положении “0”). Вероятность ложной тревоги вычисляется как отношение числа ошибочных решений N_i к общему числу испытаний за время Тн: ^* = N_i / N^*.

При N^*   оценки ^* и D^* стремятся к своим истинным значениям  и D. Следовательно, результаты измерений тем точнее, чем больше время измерения. Отношение N_i/N^* измеряется частотомером. Для этого импульсы с выхода приемника N_i подаются на вход А, а с выхода N^* - на вход Б частотомера. Переключатель частотомера “Род работы” устанавливается в положение “Отношение частот A/B”. Время измерения Тн задается переключателем “Время счета”. При этом на цифровом индикаторе частотомера будет высвечиваться значение ^* или D^* в зависимости от положения переключателя П₁.

Рекомендуется регистрировать значения  и D при одном и том же значении порога С^*. Для этого при фиксированном значении порога С^* переключатель П₁ поставить в положение “Сигн.+Шум” и манипулировать переключателем П₂ .

Для того, чтобы вычислить значение порога триггера Шмидта приведем правило решения (4.16) к виду

.

Выходное напряжение интегратора pавно

Здесь К постоянный множитель, учитывающий коэффициент передачи перемножителя и интегратора. Поэтому величина порога С_Т^* триггера Шмидта связана с порогом С выражением

(6.1)

Значение К для каждой установки написано на передней панели.

2. В пункте 8 ЗАДАНИЯ необходимо построить правила ₁ , ₂ , ₃ проверки гипотез о состоянии источника. Согласно правилу _j интервал значений порогов (С_min^* , C_max^* ) разбивается точкой С_j на область (С_min ^*, C_j ) - приема гипотезы Н₀ , и область (С_j , C_max^* ) - приема гипотезы Н₁ . Примем С₂ = С_Б , где С_Б - порог Байеса, найденный в пункте 7, а пороги C₁ и С₃ определим по формулам

C₁ = С₂ - k₀ (С₂ - С_min ) , C₃ = С₂ + k₀ (С_max - С₂ ) ,

где 0 < k₀ < 1 и задается преподавателем.

3. При расчетах вероятностей  , D=1- и порога С можно воспользоваться как экспериментальными данными , так и построенными графиками. Погрешность представления , D и С зависит от качества интерполяции и качества построения графиков. Вероятности  и D по графику определяются следующим образом:

- для известного С в произвольном месте чертежа под углом  к оси абсцисс проводится прямая, удовлетворяющая уравнению tg  = C ,

- построенная прямая переносится параллельно самой себе до касания с выбранной рабочей характеристикой,

- в точке касания определяются вероятности  и D.

З А Д А Н И Е

1. Ознакомиться с описанием экспериментальной установки, методикой эксперимента, получить от преподавателя значения априорной вероятности P₀ состояния источника, матрицу потерь П, отношение сигнал/шум и коэффициент k₀ .

2. Поставить переключатель П₁ в положение “Сигн.”. Какому состоянию канала соответствует это положение ?

Поставить переключатель П₂ в положение “Е₁ “.

Пронаблюдать и зарисовать осциллограммы напряжений в контрольных точках КТ₁, КТ₂ , КТ₃. Объяснить изменение формы сигнала в контрольной точке КТ₃ при изменении порога.

Измерить амплитуду и длительность радиосигнала в контрольной точке КТ₁ во всех положениях переключателя П₂ . По результатам измерений вычислить энергию сигнала E _s .

3. Поставить переключатель П₁ в положение “Сигн.+Шум”.

Пронаблюдать форму напряжений в тех же точках при положениях Е₁, Е₂, Е₃ переключателя П₂. Какому состоянию канала соответствует эти положения ?

Для каждого положения переключателя П₂ вычислить отношение сигнал/шум. В положении переключателя П₂ “0” пронаблюдать форму напряжений в контрольных точках. Объяснить изменение формы сигналов в точке КТ₃ при изменении порога.

4. Снять зависимость вероятности правильного обнаружения D и вероятности ошибки  от величины порога при трех значениях отношения сигнал/шум.

5. По полученным данным построить рабочие характеристики приемника на плоскости (, D) для трех значений отношения сигнал/шум, пересчитав предварительно пороги С_Т^* триггера Шмидта в пороги С, пользуясь соотношением (6.1).

* Расчет вероятностей ошибок _i , _i для различных правил  принятия решения по заданному преподавателем энергии сигнала и рассчитанным порогам триггера Шмидта С_Тi произвести по схеме

6. Вычислить вероятности  и D по формулам (5.10) и (5.11) для заданного преподавателем отношения сигнал/шум при тех же значениях порогов, что и в пункте 5.

Построить теоретическую рабочую характеристику на том же графике, что и экспериментальная рабочая характеристика и сравнить теоретическую кривую с экспериментальной.

7. Критерий Байеса. Для заданной преподавателем матрицы потерь П, априорного распределения состояния источника P₀ и отношения сигнал/шум построить средний риск как функцию порога по формуле (2.7), приведя его к виду

R(C) = P₁ П₁₁ + P₀ П₀₀ +  (С) P₀ (П₁₀ - П₀₀) - D(C) P₁ (П₀₁ - П₁₁).

Определить порог С_Б , при котором функция риска достигает минимум, и соответствующие ему вероятности  и D .

Для найденных  и D проверить формулу (3.16).

8. Минимаксный критерий. Задать три правила ₁ , ₂ , ₃ проверки гипотез о состоянии источника. Выбрать наилучшее правило.

9. Критерий максимума апостериорной вероятности. По заданной априорной вероятности P₀ состояния источника для каждого отношения сигнал/шум по экспериментальным кривым найти пороги С_{МАВ i} и вероятности ((d_i), D(d_i)), соответствующие им. Построить график D(d_i) и объяснить его поведение.

10. Критерий максимума правдоподобия. Для каждого отношения сигнал/шум по экспериментальным кривым найти пороги С_1МП , С_2МП , С_3МП и соответствующие им вероятности ((d₁) , D(d₁)), ((d₂) , D(d₂)), ((d₃), D(d₃)). Построить график С_МП(d_i) и объяснить его поведение.

11. Критерий Неймана-Пирсона. Положим вероятность ошибки первого рода равна вероятности , найденной в п. 8. Определить порог С_Н-П и вероятность правильного обнаружения D по экспериментальной кривой и теоретически для отношения сигнал/шум, заданного в п.1. Сравнить полученные результаты.

12. Построить таблицу для заданного в п.1. отношения сигнал/шум

Критерий	Априорные данные	Порог	 , D
Байеса
min max
МАВ
МП
Неймана-Пирсона

Сравнить полученные результаты. При каких условия критерии min max, МАВ. МП приводятся к критерию Байеса.

29