2.6. Минимаксный критерий

При использовании этого критерия априорной информацией является матрица потерь и функция правдоподобия.

Правила  ₁, по которым выбираются подпространства G₀ и G₁ , зависят от потребителя (они субъективны), но число k этих правил  _{j о} конечно. Для каждого правила  _j, или для каждой пары G_0j , G_1j , вычисляется условное математическое ожидание потерь - условный риск (2.5), (2.6 )

(2.24)

Из каждой пары (r _0j , r _1j) выбирается наибольший условный риск :

Получили последовательность правил и соответствующие им наибольшие условные потери. Из этой последовательности правил выбирается правило ^*, обеспечивающее минимум условного риска

. (2.25)

Рассмотрим на примере построение правила принятия решений по минимаксному критерию для параметра р биномиального распределения.

Пусть случайная величина  распределена по биномиальному закону

но наблюдателю неизвестна эта вероятность p.

Задана матрица потерь

.

Относительно параметра биномиального распределения p наблюдатель проверяет две гипотезы

H₀: p = p₀ = 0.3, H₁ : p = p₁ = 0.6

Решение о том, какая из гипотез верна, выносится на основании выборки из трех независимых реализаций случайной величины. Произведем проверку гипотез согласно минимаксному критерию.

Выборочное пространство G состоит из элементов

000 , 001 , 010 , 011 , 100 , 101 , 110 , 111 .

Зададим произвольно 2 правила разбиения пространства G (хотя их можно задать и больше)

₁: G₀₁ =(000, 010, 011): G₁₁ =(001, 100, 101, 110, 111),

₂: G₀₂ =(011, 100, 101, 110); G₁₂ =(000, 001, 010, 111).

Согласно формулам (2.5), (2.6) вычислим условные риски

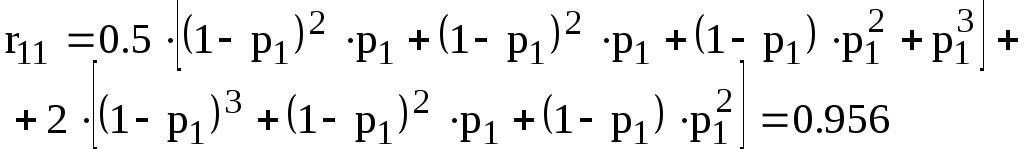
Таким образом, имеем таблицу

 j	r 0 j	r 1 j	max r i j
 1	0.7235	0.956	0.956
 2	0.874	1.292	1.292

Согласно минимакcному критерию получим

Из двух возможных правил разбиения выборочного пространства G выбираем правило ₁, обеспечивающее минимальный риск из возможных максимальных условных рисков. Для выбранного правила ₁ определим вероятности ошибок  и :

Как видно из приведенного примера, сначала выбирается способ разбиения выборочного пространства, рассчитываются условные риски, определяется правило, а затем рассчитываются вероятности ошибок.

3. Расчет вероятностей ошибок

Все рассмотренные критерии, кроме минимаксного критерия, приводят к единому правилу решения - отношение правдоподобия L(y) сравнивается с порогом, зависящим от критерия. Обозначим этот порог независимо от применяемого критерия через С. Тогда имеем правило

. (3.1)

При необходимости будем заменять величину С соответствующим порогом согласно выбранному критерию. Используем функцию правдоподобия w(y₁,y₂,...,y_m / s _i) , i=0; 1 для вычисления отношения правдоподобия по формулам (1.5), (1.6). Отношение правдоподобия примет вид

. (3.2)

Прологарифмируем (3.1) и с учетом (3.2) получим

. (3.3)

Обозначим (3.4)

Правило решения примет вид

, (3.5)

где Z - статистика,

C^* - порог, разделяющий значения статистики Z на два подпространства, соответствующих гипотезам H₀ и H₁.

Статистика Z представляет собой сумму независимых случайных значений y_i, умноженных на неслучайные величины s_i. Распределение y_i -нормальное, параметры которого зависят от состояния источника. Известно, что сумма нормально распределенных величин распределена нормально. Следовательно,

(3.6)

Определим условные математические ожидания статистики Z, учитывая, что математическое ожидание шума M[n(t_i)] = 0, дисперсия D[n(t_i)] = _n² :

(3.7)

(3.8)

(3.9)

Выразим вероятность ошибки  и вероятность правильного принятия решения D = 1- через распределение статистики Z :

 = P( L(y) > C/ s₀) = P(Z > C^* / s₀) , (3.10)

D = 1-  = P( L(y) > C / s₁) = P(Z > C^* / s₁) . (3.11)

Интегральное представление вероятностей ошибок имеет вид

На рисунке 3.1 отображено поведение условных плотностей распределения w(z/s_j) при различных состояниях источника, а также вероятности ошибок первого и второго рода. Как видно, вероятности ошибок первого и второго рода равны площади под кривой плотности распределения w(z/s_j), j=0; 1. Для явного представления вероятности ошибки первого рода подставим (3.7), (3.9) в формулу (3.6) и запишем

(3.12)

где с _ =С^*/ _z .

Подставляя (3.8), (3.9) в формулу (3.6), запишем вероятность правильного принятия решения D = 1-  :

, где c _ = (C* - a _z1 ) /  _z . (3.13)

Введем параметр d_m: . (3.14)

Выразим значения с _ и с _ через известные величины с^*, a _{z 1} ,  _z , d_m:

(3.15)

Как видно из выражений (3.12) (3.15), вероятность ошибки  и вероятность правильного принятия решения D = 1 -  являются функциями параметра d_m и порога С, который в свою очередь зависит от выбранного критерия. Если зафиксировать d_m, а порог С рассматривать как параметр, принимающий значения -  < C <  , то можно получить зависимость D=D(), которая называется рабочей характеристикой. Ее можно построить, используя (3.12), (3.13). На рисунке 3.2 показан график D=D() для d_m2 > d_m1 .

В теории статистических решений доказывается, что

(3.16)

т.е. тангенс угла наклона касательной к кривой рабочей характеристики в некоторой точке ( , D) равен порогу обнаружения С. Таким образом, для заданных двух величин из четырех параметров  , D, С, и d_m с помощью рабочей характеристики можно найти два других параметра.