2.4. Критерий и правило максимума отношения

правдоподобия

Положим априорная информация отсутствует и известны только функции правдоподобия. Критерием принятия решения в данном случае будет наибольшая условная вероятность получения выборки y₁,y₂,...,y_m при различных состояниях источника.

Сравнивая вероятности получения выборки y₁,y₂,...,y_m = y при различных состояниях источника, отдадим предпочтение той гипотезе, для которой соответствующая вероятность больше. Для двухалтьтернативных гипотез критерий максимума отношения правдоподобия представляется в виде неравенства

(2.17)

Приведем неравенство (2.17) к виду

. (2.18)

Используя функцию правдоподобия, из (2.18) получим правило принятия решения по критерию максимума отношения правдоподобия

. (2.19)

Как видно из (2.18) правило принятия решения по критерию МОП является частным случаем правила Байеса при С_Б=1.

2.5. Критерий Неймана-Пирсона и правило

принятия решений

Рассмотренные ранее критерии принятия решения не учитывали вероятности ошибок  и  при разбиении пространства G на подпространства G₀ и G₁. В критерии Неймана-Пирсона вероятности ошибок  и  играют ключевую роль. Согласно критерию Неймана-Пирсона при априорно заданной вероятности ошибки первого рода  и заданном объеме выборки m находится такая критическая область G₁, для которой вероятность 1-  принимает наибольшее значение.

Зафиксируем вероятность ошибки . Существует множество критических областей G _1i , для которых вероятность ошибки  одна и та же, т.е.

 = P((y₁,y₂,...,y_m)  G _1i / s ₀) , i = 1,2,...,

но вероятности 1-  правильного решения для различных критических областей различны.

По теореме Неймана-Пирсона среди всех возможных критических областей G_1i , для которых вероятность ошибки первого рода равна , вероятность правильного решения 1-  принимает наибольшее значение для критической области G₁, состоящей из всех тех точек y₁,y₂,...,y_m , для которых

(2.20)

Порог определяется из условия

P((y₁,y₂,...,y_m)  G₁/s₀) = . ( 2.21 )

Доказательство теоремы Неймана-Пирсона основано на методе неопределенных множителей Лагранжа. Зафиксируем вероятность ошибки  = ^* = const и составим функцию Лагранжа

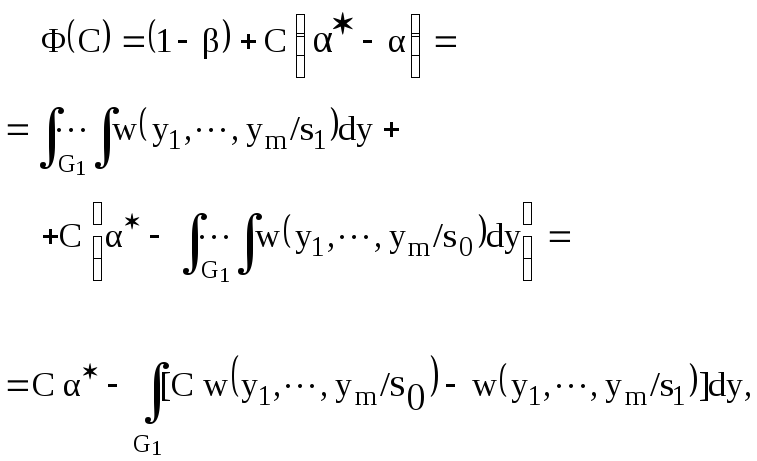
где

С - неопределенный множитель Лагранжа,

1- - максимизируемая величина,

^*-  = 0 - ограничение в виде равенства.

Вероятность 1-  достигает максимума тогда, когда достигается максимум функции Ф(С) на множестве G₁. Выберем множество y₁,y₂,...,y_m, составляющее подпространство G₁, таким образом, чтобы значение функции в квадратных скобках под интегралом в последнем выражении был бы отрицательным. Интеграл от отрицательных функций есть отрицательная величина и этим обеспечивается наибольшее значение функции Ф(С). Исходя из этого имеем

. (2.22 )

Последнее неравенство называется правилом принятия решений по критерию Неймана-Пирсона.

Согласно неравенству (2.20) решение о верности гипотезы Н₁ принимается при превышении порога С_Н-П отношением правдоподобия. Если сигнал отсутствует, то вероятность этого события равна , и она известна. Следовательно, справедливо соотношение

. (2.23)

Зная закон распределения отношения правдоподобия, можно рассчитать порог С_Н-П .