Министерство образования Российской Федерации Государственное образовательное учреждение высшего профессионального образования

СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Л.Г. Воронова, Г.Д. Коршунова, Ю.Н. Соболев

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Часть I Письменные лекции

Санкт-Петербург, 2003

2

Утверждено редакционно-издательским советом университета

УДК 621.01 (07)

Воронова Л.Г., Коршунова Г.Д., Соболев Ю.Н. Cопротивления материалов.

Ч.I: Письменные лекции. – СПб.: СЗТУ, 2003. – 126 с.

Данное учебное пособие в виде письменных лекций соответствует требованиям государственных образовательных стандартов высшего профессионального образования по направлениям подготовки дипломированного специалиста 657300 (специальность 120100 – «Технология машиностроения»), 651400 (специальность 120800 – «Материаловедение в машиностроении»), 653300 (специальность 170900 – «Подъемно-транспортные, строительные, дорожные машины и оборудование»), 653400 (специальность 240100 – «Организация перевозок и управление на транспорте») и направлениям подготовки бакалавра

552900,551800,551600, 551400.

В письменных лекциях Ч.I изложены основные разделы курса сопротивления материалов, связанные с теорией напряженного состояния материала, выбора допускаемых напряжений; рассмотрены простые деформации и даны методы расчетов конструкций на основе принятых моделей.

Письменные лекции предназначены для студентов 3 курса механических специальностей, изучающих дисциплину «Сопротивление материалов».

Рецензенты: кафедра теоретической и прикладной механики СЗТУ (зав.кафедрой В.В. Гурецкий, д-р техн. наук, проф.) ; кафедра сопротивления материалов Санкт-Петербургского государственного

морского технического университета, зав.кафедрой И.И. Курнаева, канд.техн. наук, доцент; Ю.А. Семенов, доц. кафедры ТМ и М Санкт-Петербургского государственного

технического университета.

©Северо-Западный государственный заочный технический университет, 2003

©Воронова Л.Г., Коршунова Г.Д., Соболев Ю.Н., 2003

3

ПРЕДИСЛОВИЕ

Сопротивление материалов – одна из важнейших прикладных дисциплин, изучаемых в технических вузах. На основе этой науки обеспечиваются такие элементы надежности любой машины или сооружения, как прочность, жесткость, устойчивость и другие.

Теоретические основы сопротивления материалов опираются на законы физики, методы теоретической механики, материаловедение, математику.

Необходимость выпуска методического пособия в виде письменных лекций по сопротивлению материалов диктуется тем, что далеко не все студенты, занимающиеся по очно-заочной и заочной формам обучения, имеют возможность регулярного посещения занятий. Самостоятельное изучение дисциплин связано с определенными трудностями.

Письменные лекции с графической иллюстрацией материала, примерами, ссылками на первоисточники, справочную и учебную литературу, смогут быть определенным путеводителем при самостоятельном изучении дисциплины.

Принципы, основы теории и методы сопротивления материалов, изложенные в лекциях, дают возможность использования материала в практических расчетах и решениях контрольных заданий.

Первая часть письменных лекций включает в себя сведения о механических свойствах материалов и принципах выбора допускаемых напряжений, основу теории напряженного состояния материала, теорию и характеристику простых деформаций. Особое внимание уделено деформации изгиба.

Письменные лекции разбиты по темам основного курса в соответствии с программой таким образом, что каждый новый материал основывается на изложенном ранее. Это обеспечивает представление о единстве дисциплины и связи основных теоретических представлений с законом Гука.

4

ЛЕКЦИЯ I

ЗАДАЧИ ДИСЦИПЛИНЫ «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ» МЕТОДЫ РЕШЕНИЯ

1.1.Основные теоретические положения

Основной задачей сопротивления материалов является обеспечение расчетными и экспериментальными методами основных элементов надежности машин и сооружений: прочности, жесткости, устойчивости.

Под прочностью понимается сопротивляемость деталей машин и конструкций разрушающему воздействию внешних сил.

Жесткость – неизменяемость размеров и форм под действием нагрузки, или изменение их в таких пределах, которые не отражаются на работоспособности как отдельных деталей, так и конструкции в целом.

Под устойчивостью понимается противодействие упругим деформациям (главным образом изгибу) элементов конструкций машин и сооружений, имеющих один или два больших линейных размера, под действием сжимающей нагрузки.

Обеспечение этих элементов надежности возможно при условии точного знания свойств материалов, влияния формы и размера на прочность и жесткость, учета всех сил и др. факторов, отражающихся на работе объектов. Теория и практика при решении этих задач находятся в тесном взаимодействии. Используемые конструкционные материалы обладают разными механическими свойствами, а рассчитываемые детали отличаются многообразием форм и размеров. С целью упрощения расчетов и возможности использования математического аппарата в сопротивлении материалов приняты определенные обобщения, идеализация реальных объектов и допущения, не противоречащие, впрочем, реальным условиям работы конструкций.

Реальные детали конструкций машин и сооружений с действующими на них силами представляются в виде расчетных схем, в которых конкретные детали заменяются упрощенными по форме элементами – моделями; силы рас-

5

сматриваются как сосредоточенные и распределенные. При этом характер сил – статические или динамические – принимается во внимание.

Простейшими элементами, к которым сводятся все рассматриваемые детали, являются.

Стержень или брус (плоский или пространственный) – элемент конструкции, имеющий один линейный размер, значительно больше двух других.

Пластина – элемент конструкции, имеющий два линейных размера, значительно больше третьего – толщины (мембрана, элемент обшивки).

Оболочка – криволинейная замкнутая пластина (корпус цистерны, резервуар, барабан парового котла и др.).

Массив – конструкция, имеющая три соизмеримых размера (наковальня, блок фундамента, станина станка и т.д.).

К каждому такому элементу применяются свои методы расчета. В сопротивлении материалов рассматриваются в основном расчетные схемы со стержнями, реже с пластинами, как элементами объемных конструкций. В основном же пластины, оболочки, массивы рассчитываются методами теории уп-

ругости [16], [20].

Материалы рассчитываемых деталей – моделей наделяются определенными идеализированными свойствами, обобщающими реальное поведение материалов под нагрузкой.

Так считается, что:

1) все материалы обладают сплошностью и однородностью строения;

2) все материалы обладают одинаковыми механическими свойствами по трем координатным осям; 3) все материалы в определенном диапазоне действующих на них нагрузок об-

ладают идеальной упругостью – способностью восстанавливать свои формы и размеры после снятия нагрузки.

Если реальный материал имеет разные свойства по координатным осям, это оговаривается особо. Древесина, например, обладает разными прочностными характеристиками вдоль и поперек волокон. Свойства прокатного метал-

6

ла без последующей термической обработки, разные вдоль и поперек направления прокатки. Материалы с одинаковыми свойствами по осям координат называются изотропными, а с разными свойствами – анизотропными.

В основе теории сопротивления материалов лежат два важнейших понятия – напряжение и деформация, основывающихся на упругих свойствах материалов.

Напряжение – внутренние силы упругого сопротивления материала или просто внутренние силы, приходящиеся на единицу площади.

Деформация – любое изменение размеров и формы под действием внешних или внутренних сил. Здесь под внутренними силами понимаются напряжения, возникающие вследствие различного рода термического влияния, процессов рекристаллизации при химико-термической обработке и др., но не от внешней нагрузки.

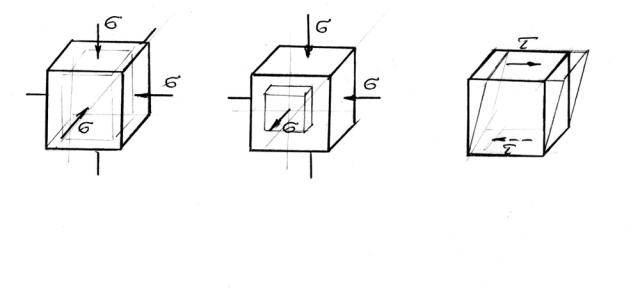
Учитывая сплошность, однородность строения материала, деформации можно рассматривать на уровне микрообъемов и реальных размеров деталей. Если мысленно выделить из объема какой-либо детали бесконечно малых размеров кубик со стороной d x, то под действием сил он может либо изменить линейные размеры, либо получить искажение формы изменением размеров граней или их скольжением друг относительно друга с изменением прямых углов (рис.1).

Рис.1 Эти линейные и угловые изменения в микрообъемах невозможно прокон-

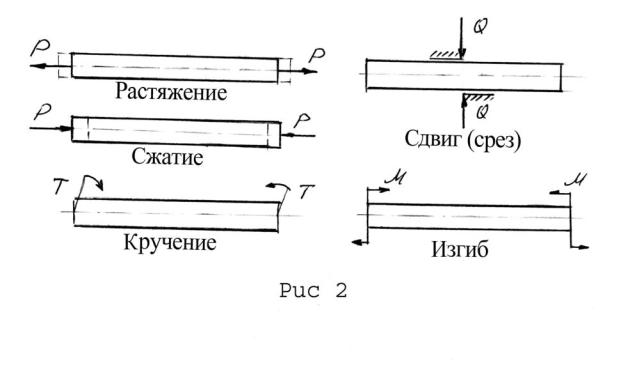
тролировать, но в объеме реальных размеров деталей они проявляются в виде деформаций типа: растяжение – сжатие, сдвиг, кручение, изгиб.

7

Эти деформации уже возможно замерить и дать заключение о напряженном состоянии материала.

Тип указанных деформаций, испытываемых деталями или элементами конструкций, зависит от относительного положения внешних сил и продольной оси стержня (модели) (рис.2).

Определение величин напряжений и деформаций, установление их значений, безопасных для работы конструкций, и составляет суть всех расчетов, выполняемых методами сопротивления материалов. Именно эти величины определяют прочность, жесткость, устойчивость.

Расчет напряжений осуществляется предварительным определением внутренних сил – равнодействующих напряжений. Внутренние силы: растягивающие и сжимающие, перерезывающие, крутящий и изгибающий моменты – это упругая реакция материала деталей машин и сооружений на действие внешних сил. Поэтому для определения их применим метод сечений с использованием уравнений статического равновесия между внутренними и внешними силами. Использование метода сечений оправдано принципом Сен-Венана, согласно которому распределение внутренних сил в материале на некотором расстоянии от места приложения нагрузки эквивалентно виду деформации, испытываемой деталью. При сложном нагружении, когда одновременно могут действовать несколько внешних сил, решение задач облегчается принципом