
Грудцына Л.Ю. ТВиМС Метод. указания
..pdf
Пример 15. С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год Y.
X |
100 |
150 |
200 |
250 |
300 |
Y |
60 |
35 |
20 |
20 |
15 |
Найти по выборке (выборка получена из нормальной генеральной совокупности): а) коэффициент линейной корреляции; б) уравнения линейной регрессии Y на X и X на Y.
Решение. Проверим а) Выборочный коэффициент линейной корреляции найдем по формуле:
r = xy - x × y . sx sy
Для этого вычислим все входящие в формулу величины (если выборка достаточно велика, то проводить вычисления удобно, предварительно составив расчетную таблицу). Объем выборки n=5.
|
|
|
|
1 |
|
|
|
|
|
|
m |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = |
|
|
|
× |
|
|
å xi |
= |
|
|
|
× (100 +150 + 200 + 250 + 300) = 200 ; |
|
|
||||||||||||||||||||||||||||||||
n |
|
5 |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
m |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
у = |
|
|
|
× |
|
å yi |
= |
|
|
|
× (60 + 35 + 20 + 20 +15) = 30 ; |
|
|
|
|
|||||||||||||||||||||||||||||||
n |
|
5 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
m |
2 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
х |
|
|
= |
|
|
|
|
|
|
|
× å x |
|
|
|
= |
|
|
|
× |
(100 |
|
+150 |
|
+ 200 |
|
+ |
250 |
|
+ 300 |
|
) = 45000 |
; |
||||||||||||||
|
|
|
n |
i |
5 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
m |
2 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
у |
|
|
= |
|
|
|
|
|
|
|
× å у |
|
|
|
= |
|
|
|
× |
(60 |
|
+ 35 |
|
+ |
20 |
|
+ |
20 |
|
+15 |
|
) = 1170; |
|
|||||||||||||
|
|
|
n |
|
i |
5 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
m |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
xy = |
|
|
|
|
|
|
|
× å xi yi = |
|
|
× (100× 60 +150×35 + 200× 20 + 250× 20 + 300×15) = 4950 ; |
|||||||||||||||||||||||||||||||||||
n |
|
|
5 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
- ( |
|
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
sx |
= |
|
|
|
|
|
x2 |
|
|
|
= |
45000 - (200)2 |
» 70,7 ; |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- ( |
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
sy |
= |
|
|
|
|
|
|
|
y2 |
|
= |
1170 - (30)2 » 16,4 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= 4950 - 200×30 » -
Коэффициент корреляции равен: r 0,91 ; r <0 – связь
70,7 ×16,4
между X (месячной зарплатой)и Y (числом уволившихся за год) является обратной; | r |≥0,7 – связь между уровнем зарплаты и числом уволившихся тесная (высокая).
51
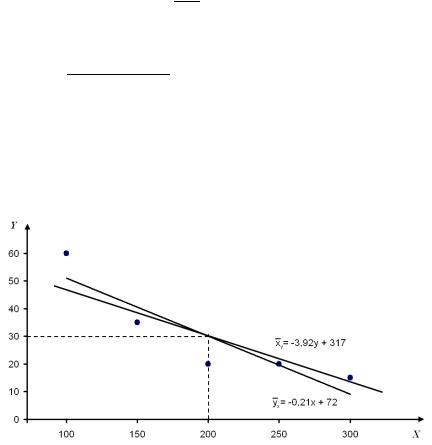
б) Найдем выборочные уравнения линейной регрессии: |
|
|||||||||
Y на X : yx = y + r × |
sy |
×(x - x) ; |
X на Y: ху = х + r × |
s |
х |
×(у |
- у) . |
|||
sx |
|
|
||||||||
|
|
|
|
|
|
sу |
|
|||
Y на X : yx = 30 |
+ (-0,91)× |
16,4 |
×(x - 200) ; |
|
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
70,7 |
|
|
|
|
|
||
|
yx = 30 |
- 0,21×(x - 200) ; |
|
|
|
|
||||
|
yx = 72 |
- 0,21× x . |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Значит, на 0,21 единицы в среднем уменьшается величина Y при увеличении Х на одну единицу.
Xна Y : ху = 200 + (-0,91) × 1670,,47 ×(у - 30) ;
ху = 200 - 3,92×(у - 30) ;
ху = 317 - 3,92× у .
Значит, на 3,92 единицы в среднем изменяется величина Х при увеличении Y на одну единицу.
Построим корреляционное поле. На координатной плоскости отмечаем все заданные пары чисел – всего 5 точек. На этом же чертеже изобразим графики прямых регрессии yx = 72 - 0,21× x и ху = 317 - 3,92× у , которые
пересекаются в точке (x, y) = (200; 30) .
52
10. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Статистической гипотезой называется любое предположение о свойствах распределения генеральной совокупности (случайной величины), которое делается на основании выборочных данных.
По своему содержанию статистические гипотезы можно подразделить на: гипотезы о виде законов распределения исследуемой случайной величины, гипотезы о числовых значениях параметров случайной величины и др.
Гипотезы обозначаются большими латинскими буквами Н0, Н1, …, Нk. Проверяемая гипотеза Н0 называется основной (нулевой). Наряду с основной Н0 рассматривается конкурирующая гипотеза Н1, которая противоречит основной. Например, если проверяется гипотеза о равенстве некоторой числовой характеристики распределения θ заданному значению θ0 (Н0: θ=θ0), то в качестве конкурирующей может быть рассмотрена одна из альтернатив: θ>θ0, θ<θ0, θ≠θ0. Выбор гипотезы Н1 определяется условиями конкретной задачи.
Принятие гипотезы или ее альтернативы основано на исследовании выборки. Правило, по которому принимается или отвергается гипотеза, называют критерием К. Статистика (наблюдаемое значение критерия) Кнабл – то значение критерия, которое вычислено по выборке.
Вероятность отвергнуть гипотезу Н0, если она верна, называется вероятностью ошибки первого рода или уровнем значимости, обозначается α. Величина γ=1-α равна вероятности принять верную гипотезу и называется
уровнем доверия.
Вероятность принять основную гипотезу, если она неверна, называется ошибкой второго рода и обозначается β. Вероятность 1-β принять гипотезу Н1, если она верна, называется мощностью критерия.
Критической областью называется совокупность значений критерия, при которых основную гипотезу Н0 отвергают. Критическая область может быть правосторонней, левосторонней, двусторонней (в зависимости от Н1).
Областью принятия гипотезы называют совокупность значений критерия, при которых Н0 принимают.
Проверка статистической гипотезы основывается на следующем принципе: если наблюдаемое значение критерия принадлежит критической области, то основную гипотезу отвергают (принимают конкурирующую); если наблюдаемое значение критерия не принадлежит критической области, то основную гипотезу принимают.
53

Критическими точками kкр называют точки, отделяющие критическую область от области принятия решений.
Для отыскания критической области задаются уровнем значимости α и определяют критические точки (по специальным таблицам).
Проверка гипотезы о значимости выборочного коэффициента корреляции
Пусть генеральная совокупность (X, Y) имеет нормальное распределение. Из этой совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции r≠0. Требуется проверить гипотезу о равенстве нулю генерального коэффициента корреляции rген.
Для того, чтобы на уровне значимости α проверить гипотезу Н0: rген=0 при конкурирующей гипотезе Н1: rген≠0, надо:
1) вычислить статистику t = r ×  n - 2 ;
n - 2 ; 
 1- r 2
1- r 2
2)по таблице значений tγ,k-критерия Стьюдента по уровню доверия
γ= 1-α и числу степеней свободы k = n-2 найти критическую точку tкр = tγ,k;
3)если | t | < tкр, то нет оснований отвергнуть основную гипотезу; если | t | > tкр, то основную гипотезу отвергают.
Пример 16. По выборке объема n=62, извлеченной из нормальной генеральной совокупности (X, Y), найден выборочный коэффициент корреляции r=0,3. На уровне значимости α=0,01 проверить гипотезу о равенстве нулю генерального коэффициента корреляции.
Решение. Проверим основную гипотезу Н0: rген=0 (конкурирующая гипотеза Н1: rген≠0). Для этого вычислим статистику:
= r × n - 2 = 0,3× 62 - 2 »
t 2,44 .

 1- r 2
1- r 2 
 1- (0,3)2
1- (0,3)2
По таблице значений tγ,k-критерия Стьюдента (см. Приложения) в
зависимости от γ = 1-α = 1-0,01 = 0,99 и k = n-2 = 62-2 = 60 находим критическое значение tкр = tγ,k = 2,66.
Так как | t |≈2,44 < tкр=2,66, то нет оснований отвергнуть основную гипотезу. Делаем вывод, что найденный по выборке коэффициент r=0,3 считать значимо отличающимся от нуля не можем.
54
ПРИЛОЖЕНИЯ
|
|
Значения функции Гаусса |
f (x) = |
1 |
|
×e−x2 / 2 |
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
2π |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Целые и |
|
|
|
|
Сотые доли x |
|
|
|
|
|
|
|
|||
десятые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
доли x |
0 |
1 |
2 |
3 |
4 |
|
5 |
|
6 |
|
|
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0,0 |
0,3989 |
0,3989 |
0,3989 |
0,3988 |
0,3986 |
|
0,3984 |
|
0,3982 |
0,3980 |
0,3977 |
0,3973 |
|||
0,1 |
3970 |
3965 |
3961 |
3956 |
3951 |
|
3945 |
|
3939 |
3932 |
3925 |
3918 |
|||
0,2 |
3910 |
3902 |
3894 |
3885 |
3876 |
|
3867 |
|
3857 |
3847 |
3836 |
3825 |
|||
0,3 |
3814 |
3802 |
3790 |
3778 |
3765 |
|
3752 |
|
3739 |
3726 |
3712 |
3697 |
|||
0,4 |
3683 |
3668 |
3653 |
3637 |
3621 |
|
3605 |
|
3589 |
3572 |
3555 |
3538 |
|||
0,5 |
3521 |
3503 |
3485 |
3467 |
3448 |
|
3429 |
|
3410 |
3391 |
3372 |
3352 |
|||
0,6 |
3332 |
3312 |
3292 |
3271 |
3251 |
|
3230 |
|
3209 |
3187 |
3166 |
3144 |
|||
0,7 |
3123 |
3101 |
3079 |
3056 |
3034 |
|
3011 |
|
2989 |
2966 |
2943 |
2920 |
|||
0,8 |
2S97 |
2874 |
2850 |
2827 |
2803 |
|
2780 |
|
2756 |
2732 |
2709 |
2685 |
|||
0,9 |
2661 |
2637 |
2613 |
2589 |
2565 |
|
2541 |
|
2516 |
2492 |
2468 |
2444 |
|||
1,0 |
0,2420 |
0,2396 |
0,2371 |
0,2347 |
0,2323 |
|
0,2299 |
|
0,2275 |
0,2251 |
0,2227 |
0,2203 |
|||
1,1 |
2179 |
2155 |
2131 |
2107 |
2083 |
|
2059 |
|
2036 |
2012 |
1989 |
1965 |
|||
1,2 |
1942 |
1919 |
1895 |
1872 |
1849 |
|
1826 |
|
1804 |
1781 |
1758 |
1736 |
|||
1,3 |
1714 |
1691 |
1669 |
1647 |
1626 |
|
1604 |
|
1582 |
1561 |
1539 |
1518 |
|||
1,4 |
1497 |
1476 |
1456 |
1435 |
1415 |
|
1394 |
|
1374 |
1354 |
1334 |
1315 |
|||
1,5 |
1295 |
1276 |
1257 |
1238 |
1219 |
|
1200 |
|
1182 |
1163 |
1145 |
1127 |
|||
1,6 |
1109 |
1092 |
1074 |
1057 |
1040 |
|
1023 |
|
1006 |
0989 |
0973 |
0957 |
|||
1,7 |
0940 |
0925 |
0909 |
0893 |
0878 |
|
0863 |
|
0848 |
0833 |
0818 |
0804 |
|||
1,8 |
0790 |
0775 |
0761 |
0748 |
0734 |
|
0721 |
|
0707 |
0694 |
0681 |
0669 |
|||
1,9 |
0656 |
0644 |
0632 |
0620 |
0608 |
|
0596 |
|
0584 |
0573 |
0562 |
0551 |
|||
2 |
0,054 |
0,0529 |
0,0519 |
0,508 |
0,0498 |
|
0,0488 |
|
0,0478 |
0,0468 |
0,0459 |
0,0449 |
|||
2,1 |
0440 |
0431 |
0422 |
0413 |
0404 |
|
0396 |
|
0387 |
0379 |
0371 |
0363 |
|||
2,2 |
0355 |
0347 |
0339 |
0332 |
0325 |
|
0317 |
|
0310 |
0303 |
0297 |
0290 |
|||
2,3 |
0283 |
0277 |
0270 |
0264 |
0258 |
|
0252 |
|
0246 |
0241 |
0235 |
0229 |
|||
2,4 |
0224 |
0219 |
0213 |
0208 |
0203 |
|
0198 |
|
0194 |
0189 |
0184 |
0180 |
|||
2,5 |
0175 |
0171 |
0167 |
0163 |
0158 |
|
0154 |
|
0151 |
0147 |
0143 |
0139 |
|||
2,6 |
0136 |
0132 |
0129 |
0126 |
0122 |
|
0119 |
|
0116 |
0113 |
0110 |
0107 |
|||
2,7 |
0104 |
0101 |
0099 |
0096 |
0093 |
|
0091 |
|
0088 |
0086 |
0084 |
0081 |
|||
2,8 |
0079 |
0077 |
0075 |
0073 |
0071 |
|
0069 |
|
0067 |
0065 |
0063 |
0061 |
|||
2,9 |
0060 |
0058 |
0056 |
0055 |
0053 |
|
0051 |
|
0050 |
0048 |
0047 |
0046 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55
Целые и |
|
|
|
|
|
|
|
|
|
Сотые доли x |
|
|
|
|
|
|
|
|
|
|
||
десятые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
доли x |
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
7 |
|
8 |
9 |
|||||||
3 |
0,0044 |
0,0043 |
0,0042 |
0,0041 |
0,0039 |
0,0038 |
0,0037 |
0,0036 |
|
0,0035 |
0,0034 |
|||||||||||
3,1 |
0033 |
0032 |
0031 |
0030 |
0029 |
0028 |
0027 |
0026 |
|
0025 |
0025 |
|||||||||||
3,2 |
0024 |
0023 |
0022 |
0022 |
0021 |
0020 |
0020 |
0019 |
|
0018 |
0018 |
|||||||||||
3,3 |
0017 |
0017 |
0016 |
0016 |
0015 |
0015 |
0014 |
0014 |
|
0013 |
0013 |
|||||||||||
3,4 |
0012 |
0012 |
0012 |
0011 |
0011 |
0010 |
0010 |
0010 |
|
0009 |
0009 |
|||||||||||
3,5 |
0009 |
0008 |
0008 |
0008 |
0008 |
0007 |
0007 |
0007 |
|
0007 |
0006 |
|||||||||||
3,6 |
0006 |
0006 |
0006 |
0005 |
0005 |
0005 |
0005 |
0005 |
|
0005 |
0004 |
|||||||||||
3,7 |
0004 |
0004 |
0004 |
0004 |
0004 |
0004 |
0003 |
0003 |
|
0003 |
0003 |
|||||||||||
3,8 |
0003 |
0003 |
0003 |
0003 |
0003 |
0002 |
0002 |
0002 |
|
0002 |
0002 |
|||||||||||
3,9 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
0002 |
|
0001 |
0001 |
|||||||||||
4 |
0,0001 |
0,0001 |
0,0001 |
0,0001 |
0,0001 |
0,0001 |
0,0001 |
0,0001 |
|
0,0001 |
0,0001 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
||||
|
|
Значения функции Лапласа F(x) = |
|
×òe−t 2 / 2dt |
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2π |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Целые и |
|
|
|
|
|
|
|
|
|
Сотые доли x |
|
|
|
|
|
|
|
|
|
|
||
десятые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
доли x |
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
6 |
|
|
|
7 |
|
8 |
9 |
|||
0,0 |
0,0000 |
0,0080 |
0,060 |
0,0239 |
0,0319 |
0,0399 |
0,0478 |
0.0558 |
|
0,0638 |
0,0717 |
|||||||||||
0,1 |
0,0797 |
0,0876 |
0,0955 |
0,1034 |
0,1113 |
0,1192 |
0,1271 |
0,1350 |
|
0,1428 |
0,1507 |
|||||||||||
0,2 |
0,1585 |
0,1663 |
0,1741 |
0,1819 |
0,1897 |
0,1974 |
0,2051 |
0,2128 |
|
0,2205 |
0,2282 |
|||||||||||
0,3 |
0,2358 |
0,2434 |
0,2510 |
0,2586 |
0,2661 |
0,2737 |
0,2812 |
0,2886 |
|
0,2960 |
0,3035 |
|||||||||||
0,4 |
0,3108 |
0,3182 |
0,3255 |
0,3328 |
0,3401 |
0,3473 |
0,3545 |
0,3616 |
|
0,3688 |
0,3759 |
|||||||||||
0,5 |
0,3829 |
0,3899 |
0,3969 |
0,4039 |
0,4108 |
0,4177 |
0,4245 |
0,4313 |
|
0,4381 |
0,4448 |
|||||||||||
0,6 |
0,4515 |
0,4581 |
0,4647 |
0,4713 |
0,4778 |
0,4843 |
0,4907 |
0,4971 |
|
0,5035 |
0,5098 |
|||||||||||
0,7 |
0,5161 |
0,5223 |
0,5285 |
0,5346 |
0,5407 |
0,5467 |
0,5527 |
0,5587 |
|
0,5646 |
0,5705 |
|||||||||||
0,8 |
0,5163 |
0,5821 |
0,5878 |
0,5935 |
0,5991 |
0,647 |
0,6102 |
0,6157 |
|
0,6211 |
0,6265 |
|||||||||||
0,9 |
0,6319 |
0,6372 |
0,6324 |
0,6476 |
0,6528 |
0,6579 |
0,6629 |
0,6679 |
|
0,6729 |
0,6778 |
|||||||||||
1,0 |
0,6827 |
0,6875 |
0,6923 |
0,6970 |
0,7017 |
0,7063 |
0,7109 |
0,7154 |
|
0,7199 |
0,7243 |
|||||||||||
1,1 |
0,7287 |
0,7330 |
0,7373 |
0,7415 |
0,7457 |
0,7499 |
0,7540 |
0,7580 |
|
0,7620 |
0,7660 |
|||||||||||
1,2 |
0,7699 |
0,7737 |
0,7775 |
0,7813 |
0,7850 |
0,7887 |
0,7923 |
0,7959 |
|
0,7984 |
0,8029 |
|||||||||||
1,3 |
0,8064 |
0,8098 |
0,8132 |
0,8165 |
0,8198 |
0,8230 |
0,8262 |
0,8293 |
|
0,8324 |
0,8355 |
|||||||||||
1,4 |
0,8385 |
0,8415 |
0,8444 |
0,8473 |
0,8501 |
0,8529 |
0,8557 |
0,8584 |
|
0,8611 |
0,8638 |
|||||||||||
1,5 |
0,8664 |
0,8690 |
0,8715 |
0,8740 |
0,8764 |
0,8789 |
0,8812 |
0,8836 |
|
0,8859 |
0,8882 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56
Целые и |
|
|
|
|
Сотые доли x |
|
|
|
|
|
десятые |
|
|
|
|
|
|
|
|
|
|
доли x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
1,6 |
0,8904 |
0,8926 |
0,8948 |
0,8969 |
0,8990 |
0,9011 |
0,9031 |
0,9051 |
0,9070 |
0,9090 |
1,7 |
0,9109 |
0,9127 |
0,9146 |
0,9164 |
0,9181 |
0,9199 |
0,9216 |
0,9233 |
0,9249 |
0,9265 |
1,8 |
0,9281 |
0,9297 |
0,9312 |
0,9327 |
0,9342 |
0,9357 |
0,9371 |
0,9385 |
0,9392 |
0,9412 |
1,9 |
0,9426 |
0,9439 |
0,9451 |
0,9464 |
0,9476 |
0,9488 |
0,9500 |
0,9512 |
0,9523 |
0,9533 |
2 |
0,9545 |
0,9556 |
0,9566 |
0,9576 |
0,9586 |
0,9596 |
0,9606 |
0,9616 |
0,9625 |
0,9634 |
2,1 |
0,9643 |
0,9651 |
0,9660 |
0,9668 |
0,9676 |
0,9684 |
0,9692 |
0,9700 |
0,9707 |
0,9715 |
2,2 |
0,9722 |
0,9729 |
0,9736 |
0,9743 |
0,9749 |
0,9756 |
0,9762 |
0,9768 |
0,9774 |
0,9780 |
2,3 |
0,9786 |
0,9791 |
0,9797 |
0,9802 |
0,9807 |
0,9812 |
0,9817 |
0,9822 |
0,9827 |
0,9832 |
2,4 |
0,9836 |
0,9841 |
0,9845 |
0,9849 |
0,9853 |
0,9857 |
0,9861 |
0,9865 |
0,9869 |
0,9872 |
2,5 |
0,9876 |
0,9879 |
0,9883 |
0,9886 |
0,9889 |
0,9892 |
0,9895 |
0,9898 |
0,9901 |
0,9904 |
2,6 |
0,9907 |
0,9910 |
0,9912 |
0,9915 |
0,9917 |
0,9920 |
0,9922 |
0,9924 |
0,9926 |
0,9928 |
2,7 |
0,9931 |
0,9933 |
0,9935 |
0,9937 |
0,9939 |
0,9940 |
0,9942 |
0,9944 |
0,9946 |
0,9947 |
2,8 |
0,9949 |
0,9951 |
0,9952 |
0,9953 |
0,9955 |
0,9956 |
0,9958 |
0,9959 |
0,9960 |
0,9961 |
2,9 |
0,9963 |
0,9964 |
0,9965 |
0,9966 |
0,9967 |
0,9968 |
0,9969 |
0,9970 |
0,9971 |
0,9972 |
3 |
0,9973 |
0,9974 |
0,9975 |
0,9976 |
0,9976 |
0,9977 |
0,9978 |
0,9979 |
0,9979 |
0,9980 |
3,1 |
0,9981 |
0,9981 |
0,9982 |
0,9983 |
0,9983 |
0,9984 |
0,9984 |
0,9985 |
0,9985 |
0,9986 |
3,2 |
0,9986 |
0,9987 |
0,9987 |
0,9988 |
0,9988 |
0,9989 |
0,9989 |
0,9989 |
0,9990 |
0,9990 |
3,3 |
0,9990 |
0,9991 |
0,9991 |
0,9991 |
0,9992 |
0,9992 |
0,9992 |
0,9992 |
0,9993 |
0,9993 |
3,4 |
0,9993 |
0,9994 |
0,9994 |
0,9994 |
0,9994 |
0,9994 |
0,9995 |
0,9995 |
0,9995 |
0,9995 |
3,5 |
0,9995 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9996 |
0,9997 |
0,9997 |
3,6 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9997 |
0,9998 |
0,9998 |
0,9998 |
3,7 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
0,9998 |
3,8 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
3,9 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
4 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
0,9999 |
|
|
|
|
|
|
|
|
|
|
|
57
Значения tγ,k-критерия Стьюдента
Число |
|
|
|
|
|
Вероятность γ |
|
|
|
|
||
степеней |
|
|
|
|
|
|
|
|
|
|
|
|
свободы k |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
1 |
0,16 |
0,32 |
0,51 |
0,73 |
1,00 |
1,38 |
1,96 |
3,08 |
6,31 |
12,71 |
31,82 |
63,66 |
2 |
14 |
29 |
44 |
62 |
0,82 |
06 |
34 |
1,89 |
2,92 |
4.30 |
6,96 |
9,92 |
3 |
14 |
28 |
42 |
58 |
76 |
0,98 |
25 |
64 |
35 |
3,18 |
4,54 |
5,84 |
4 |
13 |
27 |
41 |
57 |
74 |
94 |
19 |
53 |
13 |
2,78 |
3,75 |
4,60 |
5 |
13 |
27 |
41 |
56 |
73 |
92 |
16 |
48 |
01 |
57 |
36 |
03 |
6 |
0,13 |
0,26 |
0,40 |
0,55 |
1,72 |
1,91 |
1,13 |
1,44 |
1,94 |
2,45 |
3,14 |
3,71 |
7 |
13 |
26 |
40 |
55 |
71 |
90 |
12 |
41 |
89 |
36 |
00 |
50 |
8 |
13 |
26 |
40 |
55 |
70 |
89 |
11 |
40 |
86 |
31 |
2,90 |
35 |
9 |
13 |
26 |
40 |
54 |
70 |
88 |
10 |
38 |
83 |
26 |
82 |
25 |
10 |
13 |
26 |
40 |
54 |
70 |
88 |
09 |
37 |
81 |
23 |
76 |
17 |
11 |
0,13 |
0,26 |
0,40 |
0,54 |
0,70 |
0,88 |
1,09 |
1,36 |
1,80 |
2,20 |
2,72 |
3,11 |
12 |
13 |
26 |
39 |
54 |
69 |
87 |
08 |
36 |
78 |
18 |
68 |
05 |
13 |
13 |
26 |
39 |
54 |
69 |
87 |
08 |
35 |
77 |
16 |
65 |
01 |
14 |
13 |
26 |
39 |
54 |
69 |
87 |
08 |
34 |
76 |
14 |
62 |
2,98 |
15 |
13 |
26 |
39 |
54 |
69 |
87 |
07 |
34 |
75 |
13 |
60 |
95 |
16 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,07 |
1,34 |
1,75 |
2,12 |
2,58 |
2,92 |
17 |
13 |
26 |
39 |
53 |
69 |
86 |
07 |
33 |
74 |
11 |
57 |
90 |
18 |
13 |
26 |
39 |
53 |
69 |
86 |
07 |
33 |
73 |
10 |
55 |
88 |
19 |
13 |
26 |
39 |
53 |
69 |
86 |
07 |
33 |
73 |
09 |
54 |
86 |
20 |
13 |
26 |
39 |
53 |
69 |
86 |
06 |
32 |
72 |
09 |
53 |
84 |
21 |
0,13 |
0,26 |
0,39 |
0,53 |
0,69 |
0,86 |
1,06 |
1,32 |
1,72 |
2,08 |
2,52 |
2,83 |
22 |
13 |
26 |
39 |
53 |
69 |
86 |
06 |
32 |
72 |
07 |
51 |
82 |
23 |
13 |
26 |
39 |
53 |
68 |
86 |
06 |
32 |
71 |
07 |
50 |
81 |
24 |
13 |
26 |
39 |
53 |
68 |
86 |
06 |
32 |
71 |
06 |
49 |
80 |
25 |
13 |
26 |
39 |
53 |
68 |
86 |
06 |
32 |
71 |
06 |
48 |
79 |
26 |
0,13 |
0,26 |
0,39 |
0,53 |
0,68 |
0,86 |
1,06 |
1,31 |
1,71 |
2,06 |
2,48 |
2,78 |
27 |
13 |
26 |
39 |
53 |
68 |
85 |
06 |
31 |
70 |
05 |
47 |
77 |
28 |
13 |
26 |
39 |
53 |
68 |
85 |
06 |
31 |
70 |
05 |
47 |
76 |
29 |
13 |
26 |
39 |
53 |
68 |
85 |
05 |
31 |
70 |
04 |
46 |
76 |
30 |
13 |
26 |
39 |
53 |
68 |
85 |
05 |
31 |
70 |
04 |
46 |
75 |
40 |
0,13 |
0,25 |
0,39 |
0,53 |
0,68 |
0,85 |
1,05 |
1,30 |
1,68 |
2,02 |
2,42 |
2,70 |
60 |
13 |
25 |
39 |
53 |
68 |
85 |
05 |
30 |
67 |
00 |
39 |
66 |
120 |
0,13 |
0,25 |
0,39 |
0,53 |
0.68 |
0,84 |
1,04 |
1,29 |
1,66 |
1,98 |
2,36 |
2,62 |
∞ |
13 |
25 |
38 |
52 |
67 |
84 |
04 |
28 |
64 |
96 |
33 |
58 |
58
ЛИТЕРАТУРА
1.Кремер Н.Ш. Теория вероятностей и математическая статистика : учебник для вузов / Н.Ш. Кремер. – М. : ЮНИТИ-ДАНА, 2004. – 543с. –
Гриф МО. – ISBN 5-238-00333-1.
2.Елисеева И.И. Теория статистики с основами теории вероятностей : учеб. пособие для вузов / И.И. Елисеева, В.С. Князевский, Л.И. Ниворожкина.
–М. : ЮНИТИ-ДАНА, 2001. – 446с. – Гриф МО. – ISBN 5-238-00132-0.
3.Красс М.С. Математика в экономике. Математические методы и модели : учебник для вузов / М.С. Красс, Б.П. Чупрынов. — М. : Финансы и статистика, 2007. – 541с. – Гриф МО. – ISBN 978-5-279-03071-2.
4.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике : учебник для вузов / В.Е. Гмурман. – М. :
Высшая школа, 2003. – 400с. – Гриф МО. – ISBN 5-06-004212-Х.
5.Белько И.В. Теория вероятностей и математическая статистика. Примеры и задачи : учеб. пособие / И.В Белько, Г.П. Свирид. – Минск. : Новое знание, 2004. – 251с. – Гриф МО Республики Беларусь. – ISBN 985- 475-102-3.
6.Мацкевич И.П. Сборник задач и упражнений по высшей математике. Теория вероятностей и математическая статистика : учеб. пособие / И.П. Мацкевич, Г.П. Свирид, Г.М. Булдык. – Мн. : Выш. шк., 1996. – 340с. – Гриф МО Республики Беларусь. – ISBN 985-06-0038-1.
59
Учебное издание
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические указания к выполнению контрольной работы
Грудцына Лариса Юрьевна
Технический редактор
Подписано в печать ... .
Формат 60x84 1/16.
Печать ризографическая.
Усл. печ. л...
Тираж ... экз. Заказ №...
Лаборатория оперативной полиграфии филиала Казанского (Приволжского) федерального университета в г. Набережные Челны.
423812, Республика Татарстан, г. Набережные Челны, пр. Сююмбике, 10 А (11/29),
тел/факс (8552) 58-88-94, 51-87-34, е-mail: nauka@ksuchelny.ru.
