Грудцына Л.Ю. ТВиМС Метод. указания

Статистический ряд с соответствующими частостями представляет собой

Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную линию, соединяющую точки плоскости с координатами (xi, ni), i=1, 2, … m. Можно также построить полигон, где точками являются пары чисел (xi, wi).

Средние величины характеризуют значение признака, вокруг которого концентрируются наблюдения или, как говорят, центральную тенденцию распределения.

Выборочной средней (средней арифметической) статистического ряда называется сумма произведений всех вариантов на соответствующие частоты,

~

Медианой Ме называется значение признака, приходящегося на середину упорядоченного ряда наблюдений.

Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, для ряда с четным числом членов – полусумме двух серединных вариантов.

Замечание 1. Небольшое количество наблюдений, лежащих далеко от центра ряда, могут сильно искажать значение средней арифметической величины, поэтому при изучении “средних показателей” необходимо использовать и медиану. Медиана, в отличие от выборочной средней, устойчива по отношению к крайним значениям ряда.

~

Модой Мо называется вариант, которому соответствует наибольшая частота.

Средние величины, рассмотренные выше, не отражают изменчивости (вариации) значения признака. Простейшим показателем является вариационный размах – разность между наибольшим и наименьшим вариантами: R=xmax–xmin.

41

Интерес представляют меры вариации наблюдений вокруг средних величин.

Выборочной дисперсией называется средняя арифметическая квадратов отклонений вариантов от их выборочной средней:

Чтобы мера вариации была выражена в тех же единицах, что и значения признака, вычисляют среднее квадратическое отклонение:

s = 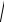х2 - (х)2 .

Замечание 2. Для несгруппированных рядов при расчете выборочных средней и дисперсии соответствующие формулы упрощаются с учетом того,

что ni = 1 ( i = 1, 2, ... , n ).

Пример 12. Выборка задана в виде распределения частот:

Найти: а) распределение относительных частот; б) выборочные среднее и дисперсию.

Решение. а) Найдем объем выборки: n = 1+3+6 = 10.

Найдем относительные частоты: w1=1/10=0,1; w2=3/10=0,3; w3=6/10=0,6.

Запишем распределение относительных частот:

42

Выборочная дисперсия:

Если наблюдаемая случайная величина непрерывна или дискретная величина такова, что число ее возможных значений велико, то для построения статистического ряда используют интервальный ряд распределения.

Интервальным статистическим рядом называется упорядоченная последовательность интервалов варьирования случайной величины с соответствующими частотами (или частостями).

Для построения такого ряда весь возможный интервал варьирования разбивают на конечное число частичных интервалов [ai, ai+1) и подсчитывают частоту ni попадания значений величины в каждый частичный интервал.

Рекомендуется количество интервалов выбирать по формуле Стерджеса: m=1+1,4·ln n.

Длина частичного интервала равна k = xmax - xmin . 1+1,4 ×ln n

Если вариант находится на границе частичного интервала, то при подсчете частот его присоединяют только к одному из интервалов.

Для графического изображения интервальных вариационных рядов используют гистограмму и кумуляту.

Гистограмма – ступенчатая фигура из прямоугольников с основаниями, равными длине интервалов k, и высотами, равными частотам ni (или частостям wi) интервалов.

Кумулята – кривая накопленных частот (частостей).

Для дискретного ряда кумулята представляет собой ломаную, соединяющую точки (xi , nxi ) (или точки (xi , wxi ) ), где nxi – накопленные

частоты ( wxi – частости).

Для интервального ряда кумулята соединяет точки (аi , nаi ) . Ломаная начинается с точки, соответствующей началу первого интервала а1

43

(накопленная частота nа1 равна нулю), другие точки этой ломаной

соответствуют концам интервалов.

Эмпирической функцией распределения Fn(x) называется частость того,

что признак примет значение, меньшее заданного х, т.е. значение функции в точке x равно накопленной частости: Fn(x) = w(X<х) = wx.

Эмпирическая функция распределения – аналог известной функции распределения случайной величины Х.

Для интервального статистического ряда графиком эмпирической функции распределения является кумулята.

Основными числовым характеристикам любого статистического ряда являются выборочные среднее, дисперсия и среднее квадратическое отклонение. Для вычисления этих характеристик интервального ряда применяются формулы, приведенные выше, только в качестве xi берется середина частичного интервала [ai, ai+1), где i = 1, 2, ... , m (m – число

интервалов).

Мода интервального статистического ряда может быть приближенно найдена графическим путем с помощью гистограммы. На гистограмме распределения находят прямоугольник с наибольшей частотой. Соединяя отрезками прямых вершины этого прямоугольника с соответствующими вершинами двух соседних прямоугольников, получают точку пересечения, абсцисса которой будет модой ряда.

Медиану интервального статистического ряда можно найти графическим путем с помощью кумуляты как значение признака, для которого nхi = n / 2

или wхi = 1/ 2 .

Пример 13. В таблице приведены значения прибыли (в тыс. усл.ед) пятидесяти торговых точек, принадлежащих одной фирме.

Построить интервальный статистический ряд и изобразить его графически в виде гистограммы.

Решение. По данным выборки xmin=3,017; xmax=14,910.

44

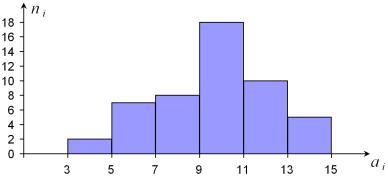
Размах выборки R=xmax–xmin=14,910-2,917=11,893.

Разобьем множество значений n=50 на интервалы. Число интервалов по

Для удобства вычислений выберем m=6, k=2. Началом первого интервала возьмем ближайшее целое к наименьшему варианту, т.е. а1=3, тогда конец последнего, шестого, интервала а8=15.

Подсчитывая число вариантов, попадающих в каждый интервал, получим следующий интервальный статистический ряд.

По данным таблицы строим гистограмму – ступенчатую фигуру, отмечая на горизонтальной оси концы частичных интервалов ai, на вертикальной оси

– соответствующие частоты ni.

8. ОЦЕНКА ПАРАМЕТРОВ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

Выборочный метод

В практике статистических наблюдений различают два вида наблюдений: сплошное (анализу подлежит вся генеральная совокупность) и выборочное (изучается часть объектов, выборка).

45

Сущность выборочного метода заключается в том, чтобы по определенной части генеральной совокупности (выборке) судить о ее свойствах в целом.

Выборочный метод является единственно возможным в случае бесконечной генеральной совокупности или когда исследование связано с уничтожением наблюдаемых объектов. Для того, чтобы по выборке можно было адекватно судить о случайной величине, она должна быть представительной (репрезентативной). Репрезентативность выборки обеспечивается случайностью отбора ее элементов, т.к. все элементы генеральной совокупности должны иметь одинаковую вероятность попадания в выборку.

Имеются два способа образования выборки:

1)повторная выборка, когда каждый элемент, случайно отобранный и исследованный, возвращается в общую совокупность и может быть отобран повторно;

2)бесповторная выборка, когда отобранный элемент не возвращается в общую совокупность.

Точечная оценка

Числовые характеристики генеральной совокупности называются генеральными параметрами.

Когда говорят о теоретическом распределении, то обычно определяют его при помощи параметров функции распределения. Например, параметрами нормального распределения являются математическое ожидание и среднее квадратическое отклонение. В теории выборочного метода аналогами этих

понятий являются генеральная средняя xген и генеральная дисперсия σ ген2 .

Статистический вывод о параметрах генеральной совокупности основан на выборочных характеристиках. Характеристики, получаемые по различным выборкам, как правило, отличаются друг от друга. Вообще говоря, нельзя по выборке определить точное значение генерального параметра, можно лишь найти его приближенное значение.

Оценка параметра – определенная числовая характеристика, полученная из выборки. Когда одно отдельное значение используется для оценки, то такая оценка называется точечной оценкой генерального параметра.

Для любых оценок важны характеристики: состоятельность и несмещенность. Состоятельность означает, что при увеличении размера

46

выборки оценка становится все более точной. Несмещенность – что при выборе любого размера оценка дает в среднем правильный результат (ее математическое ожидание равно оцениваемому параметру).

m

å xini

Выборочная средняя x = i=1 используется как оценка генеральной n

генеральной дисперсии.

Оценки x, s 2 – состоятельные и несмещенные.

Интервальная оценка

Точечная оценка θn дает лишь приближенное значение параметра θ и для выборки малого объема может существенно от него отличаться. Чтобы получить представление о точности и надежности оценки, используют интервальную оценку.

Интервальной оценкой параметра θ называется интервал (α, β), в

котором с заданной вероятностью γ содержится неизвестное значение параметра θ.

Интервал (α, β) называется доверительным интервалом, а вероятность γ

– надежностью (доверительной вероятностью).

Обычно доверительный интервал симметричен относительно оценки θn ,

вероятностью γ.

Наибольшее отклонение выборочного значения параметра от его истинного значения называется предельной ошибкой выборки.

Пусть имеется выборка n элементов из генеральной совокупности, объем

47

Доверительный интервал уровня надежности γ для генеральной

Φ(t) – функция Лапласа.

Если n≤30, то доверительный интервал строится только для нормально

находится по таблице распределения Стьюдента по вероятности γ и степеням свободы k=n-1.

Пример 14. Из партии в 5000 электрических ламп было отобрано 300 по схеме бесповторной выборки. Средняя продолжительность горения ламп в выборке равна x = 1450 (ч.), дисперсия – s 2 = 4000 . Найти доверительный интервал для среднего срока горения лампы с надежностью 0,92.

Решение. Доверительный интервал для генеральной средней

функция Лапласа. В данном случае Φ(t)=0,92 => t=1,75 (см. Приложения). По условию задачи объем генеральной совокупности N=5000, были

48

9. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ

Под двумерной случайной величиной (Х, Y) понимают совокупность случайных величин Х и Y, рассматриваемых совместно (в одном эксперименте). Каждое появление такой величины представляет собой пару чисел (х, у).

В математике для описания связи между переменными используют понятие функции (каждому значению Х ставится в соответствие единственное значение Y). Однако чаще встречаются зависимости, в которых каждому значению Х соответствует одно из множества значений Y, причем заранее неизвестно какое. Такого рода зависимость называют корреляционной. Как и функциональные, корреляционные связи могут иметь различную форму, например, линейную или криволинейную.

На практике нередко возникает необходимость узнать связаны ли между собой наблюдаемые величины, можно ли по значению одной величины предположить возможное значение другой и т.д. Для решения этих задач применяют корреляционно-регрессионный анализ.

Рассмотрим простейший случай задания экспериментальных данных (несгруппированные данные) – набор пар чисел (xi, уi), i=1, 2, … n. Здесь х1, х2, …, хn – выборка значений случайной величины Х, а у1, у2, …, уn – выборка значений Y.

Основной оценкой тесноты связи между Х и Y служит выборочный коэффициент линейной корреляции:

отклонения.

Свойства коэффициента линейной корреляции.

1.Коэффициент принимает значения на отрезке [-1;1] т.е. -1≤ r ≤1.

Взависимости от того, насколько | r | приближается к 1, различают:

а) слабую связь, если | r |≤0,3;

б) умеренную связь, если 0,3<| r |<0,7;

49

в) тесную связь, если | r |≥0,7.

2.Если r <0, то связь является обратной (с увеличением Х значения Y в среднем уменьшаются); если r >0, то связь является прямой (с увеличением Х значения Y в среднем увеличиваются).

3.Если | r |=1, то корреляционная связь между Х и Y представляет собой линейную зависимость.

Корреляционным полем называется графическое представление выборки (Х, Y) в виде точек (xi, уi), i=1, 2, … n координатной плоскости.

При умеренной или тесной связи между величинами Х и Y все точки выборки (xi, уi) располагаются вблизи прямых, называемых прямыми регрессии.

квадратические отклонения величин Х и Y; а r – выборочный коэффициент линейной корреляции.

Первая прямая представляет собой модель вида Y=F(X) где Y – зависимая

регрессии Х на Y и показывает, на сколько единиц в среднем изменяется величина Х при увеличении Y на одну единицу.

Замечание. Приведенные выше формулы справедливы лишь в случае, когда данные наблюдений (выборку) можно считать полученными из нормально распределенной генеральной совокупности.

50