
- •VI. Обработка символьной информации
- •VI.1. Операции над текстами. Простые формы обмена
- •VI.2. Ввод данных и печать результатов
- •VI.3. Символьное представление чисел
- •V.1.4. Задачи из раздела "Синтаксис и компиляция"
- •1) Вставить рисунок на стр. 22
- •2) Вставить рисунок на стр. 22
- •3) Вставить рисунок на стр. 23
- •4) Вставить рисунок на стр. 23
- •VI.5. Дополнительные задачи (трудные)
VI.3. Символьное представление чисел
В
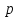 -ичной
позиционной системе счисления для
изображения
чисел используются
-ичной
позиционной системе счисления для
изображения
чисел используются
 цифр и знаки "+"
и "−".
Записи
цифр и знаки "+"
и "−".
Записи
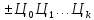 ,
,
±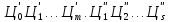 ,
,
± ,
,
где
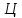 (с индексами
и штрихами) −
(с индексами
и штрихами) −
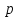 -ичные
цифры, служат
для изображения соответственно целого
числа
-ичные
цифры, служат
для изображения соответственно целого
числа

и вещественных чисел
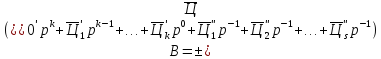
и
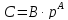 ,
,
где
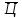 −
числовое значение цифры
−
числовое значение цифры
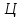 .
Отметим, что любое вещественное число
.
Отметим, что любое вещественное число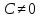 может быть представлено в виде
может быть представлено в виде ,
где
,
где
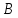 −
вещественное число, называемое мантиссой,
такое, что
−
вещественное число, называемое мантиссой,
такое, что
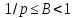 ,
а
,
а
 −
целое, называемое порядком.
Полезные сведения о различных способах
записи чисел можно подчерпнуть, например,
у Д. Кнута ([9], том 2, гл. 4).
−
целое, называемое порядком.
Полезные сведения о различных способах
записи чисел можно подчерпнуть, например,
у Д. Кнута ([9], том 2, гл. 4).
49.
(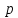 -ичные
таблицы). Напечатать
таблицы сложения и умножения чисел для
-ичные
таблицы). Напечатать
таблицы сложения и умножения чисел для
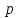 -ичной системы счисления,
-ичной системы счисления,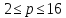 .
.
50. (Преобразования из одной формы в другую.)
а)
Преобразовать целое число
 из внутренней формы представления в
его символьное представление
из внутренней формы представления в
его символьное представление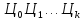 в
в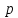 -ичной
системе счисления.
-ичной
системе счисления.
б)
Преобразовать вещественное число
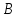
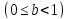 из внутренней формы представления в
его символьное представление
из внутренней формы представления в
его символьное представление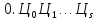 в
в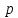 -ичной
системе счисления. Здесь
-ичной
системе счисления. Здесь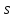 −
заданное целое число, которое показывает,
сколько цифр должно быть учтено в дробной
части.
−
заданное целое число, которое показывает,
сколько цифр должно быть учтено в дробной
части.
в)
Преобразовать вещественное число
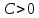 из внутренней формы представления в
из внутренней формы представления в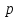 -ичной
системе счисления вида
-ичной
системе счисления вида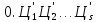
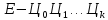 ,
где
,
где −
значащая цифра, т.е.
−
значащая цифра, т.е.
 (или, что то же самое,
(или, что то же самое,
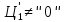 ).
).
г) Выполнить обратные преобразования.
Указания.
а)
значение цифры
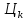 равно остатку от деления
равно остатку от деления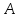 на
на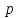 .
Остальные цифры найти нетрудно, если
учесть, что
.
Остальные цифры найти нетрудно, если
учесть, что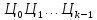 есть
есть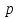 -ичное
представление числа
-ичное
представление числа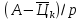 .б) Здесь
значение
.б) Здесь
значение
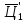 цифры
цифры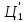 равно целой части числа
равно целой части числа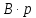 .
Чтобы найти остальные цифры следует
учесть, что
.
Чтобы найти остальные цифры следует
учесть, что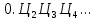 есть символьное представление числа
есть символьное представление числа .в) Для
получения тербуемого представления
сначала необходимо найти вещественное
число
.в) Для
получения тербуемого представления
сначала необходимо найти вещественное
число
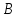 и целое
и целое такие, что
такие, что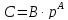 ,
,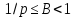 .
Тогда
.
Тогда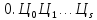 есть символьное представление
числа
есть символьное представление
числа
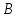 ,
а
,
а
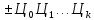 есть символьное представление числа
есть символьное представление числа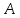 .
.
51. (Операции над числами в символьном представлении.)
а) Сложить и перемножить два целых числа вида
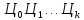
одинаковой длины.
б) Сложить и перемножить два вещественных числа вида
 ,
,
представленных
в символьном виде в
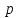 -ичной
системе счисления. Рекомендация: операции
выполнить, не переходя к внутреннему
представлению чисел−
в этом″соль″задания.
-ичной
системе счисления. Рекомендация: операции
выполнить, не переходя к внутреннему
представлению чисел−
в этом″соль″задания.
52.
(Числа-палиндромы.)
Палиндромы −
это десятичное число, читаемое одинаково
туда и обратно. Например,
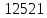 – палиндром. Возьмём любое число
– палиндром. Возьмём любое число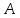 .
Если это не палиндром, то реверсируем
его цифры, т.е. запишем их в обратном
порядке. В результате получим некоторое
число
.
Если это не палиндром, то реверсируем
его цифры, т.е. запишем их в обратном
порядке. В результате получим некоторое
число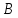 .
Вычислим
.
Вычислим
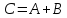 .
Если
.
Если
 − не
палиндром, то описанные действия
повторяются до тех пор пока не получим
палиндром. Проверить этот алгоритм для
чисел
− не
палиндром, то описанные действия
повторяются до тех пор пока не получим
палиндром. Проверить этот алгоритм для
чисел
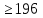 .
(Замечание.
.
(Замечание.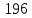 −
первое число, для которого не известно,
работает ли этот алгоритм. Указание.
Здесь могут получаться большие числа.
Поэтому их следует представить в
символьном виде, используя для этой
цели достаточно длинные массивы с
компонентами – цифрами.)
−
первое число, для которого не известно,
работает ли этот алгоритм. Указание.
Здесь могут получаться большие числа.
Поэтому их следует представить в
символьном виде, используя для этой
цели достаточно длинные массивы с
компонентами – цифрами.)
53.
(Точное
представление.)
Напечатать точное десятичное представление
несократимой, рациональной дроби
 ,
,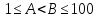 .
Периодическая часть дроби должна быть
отделена от непериодической части
пробелом или отделена скобками. Образец
печати:
.
Периодическая часть дроби должна быть
отделена от непериодической части
пробелом или отделена скобками. Образец
печати:
1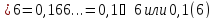
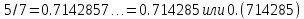

54. (Римские цифры.)
а) Записать заданное целое число римскими цифрами.
б) выполнить обратное преобразование.
Указание.
Для записи чисел в римской нотации,
которая, заметим, не является позиционной,
используются цифры I
(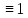 ),V (
),V (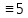 ),X (
),X ( ),L (
),L (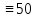 ),C (
),C (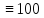 )
,D
)
,D
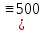 ),M (
),M (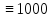 ).
Считать, что все числа не превосходят
).
Считать, что все числа не превосходят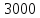 .
.
