
- •VI. Обработка символьной информации
- •VI.1. Операции над текстами. Простые формы обмена
- •VI.2. Ввод данных и печать результатов
- •VI.3. Символьное представление чисел
- •V.1.4. Задачи из раздела "Синтаксис и компиляция"
- •1) Вставить рисунок на стр. 22
- •2) Вставить рисунок на стр. 22
- •3) Вставить рисунок на стр. 23
- •4) Вставить рисунок на стр. 23
- •VI.5. Дополнительные задачи (трудные)
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет вычислительной математики и кибернетики
Кафедра теоретической кибернентики
ЗАДАЧИ
по теме
«ОБРАБОТКА СИМВОЛЬНОЙ ИНФОРМАЦИИ»
Настоящая работа предназначена для студентов, изучающих программирование на современных ЭВМ, а также для преподавателей, ведущих практические занятия по программированию. Учебный материал представлен задачами, которые рекомендуется использовать при изучении темы «Подпрограммы» (операции, функции, процедуры)».
Казань – 2011
VI. Обработка символьной информации
В этом разделе термин текст означает произвольную последовательность символов (литер). В том случае, когда длина текста заранее не фиксирована, признаком окончания текста служит символ ″¤″ (солнышко). Входной текст − это текст, подлежащий вводу (чтению) с внешнего носителя информации; выходной текст − это текст, который следует напечатать. Подразумевается, что для хранения текстов используются массивы и последовательные файлы с компонентами символьного типа.
VI.1. Операции над текстами. Простые формы обмена
1. (Палиндромы.) Текст, читаемый одинаково туда и обратно, называется палиндромом. Установить, является ли заданный текст палиндромом. (Развитие темы этой задачи см. в задачах 10 и 74.)
2. (Контекстно-свободные исключения.)
а) Исключить из текста пробелы и знаки препинания. Знаки препинания:
|
. |
, |
: |
; |
! |
″ |
‘ |
’ |
( |
) |
[ |
] |
- |
∕ |
∗ |
@ |
Пробел обозначают символом ″⊔″.
б) Часть текста, начинающаяся символом ″{″ и оканчивающаяся символом ″}″, называется комментарием. Исключить из текста комментарии.
Другой вариант задания: комментарий − это часть текста, заключенная между парами символов ″∕∗″ и ″∗∕″ (или между словом ″comment″ и ″;″).
в) Символ ″-″ используется в тексте только как корректурный знак удаления предшествующего символа. Повторное вхождение символа ″-″ означает удаление последнего (из предшествующих) ещё не удаленного символа. Переписать текст выполняя все удаления, предписанные вхождениями символа ″-″ (″-″ тоже удалить).
Поясняющий пример: текст ″-она-⊔была–⊔не--⊔права⊔⊔---.″ должен быть преобразован в текст ″он⊔был⊔⊔прав. ″.
г) Слово - это любая последовательность символов, не содержащая символа пробела. Исключить из текста слова, в которых встречается буква ″Ь″.
Ограничения на текст: слова в тексте разделены в точности одним пробелом; после очередного пробела следует либо очередное слово, либо символ окончания текста ″¤″.
3. (Контекстные исключения.)
а) Исключить из текста повторные пробелы (т.е. только те, которым непосредственно предшествуют пробелы).
б) Исключить из текста пробелы, сохранив их, однако, в комментариях (см. задачу 2 б).
в) Исключить из текста слова, начинающиеся буквой ″Ь″. Ограничения на текст те же, что и в задаче 2 г.
г) Исключить из текста слова. оканчивающиеся буквой ″Ь″. Ограничения на текст те же. что и в задаче 2 г.
д) Исключить из текста пробелы, расположенные между словами и следующими за ними знаками препинания.
е) Текст представляет собой форматированный список почтовых адресов. Каждый адрес содержит в точности 80 символов, благодаря добавленным в его конец форматирующим пробелам. Символ ″¤″ окончания текста расположен непосредственно после заключительной 80-символьной порции текста. Исключить из текста только форматирующие пробелы.
4. (Вставки, замены и перемещения.)
а) Вставить в текст пробел (если он отсутствует) после каждого знака препинания.
б) Заменить в тексте все вхождения слов ″if″, ″then″, ″else″ соответственно на слова ″если″, ″то″, ″иначе″. Ограничения на текст те же, что и в задаче 2 г.
в) Текст представляет собой (неформатированный) список почтовых адресов. Каждый адрес содержит не более 80 символов и оканчивается символом-разделителем ″∕″. Форматировать текст, вставляя в ″хвосты″ почтовых адресов пробелы так, чтобы каждый адрес содержал в точности 80 символов.
г) Символ ″∗″ используется в основном тексте только как корректурный знак вставки. Вставляемые фрагменты берутся последовательно из вспомогательного текста, причем каждый фрагмент в нём оканчивается символом-разделителем ″∕″. Осуществить коррекцию основного текста.
д) Буква ″Ь″, кроме обычного употребления, используется в основном тексте как корректурный знак: слова, начинающиеся с этой буквы, заменяются на слова, которые берутся последовательно из вспомогательного текста. Осуществить коррекцию основного текста. Ограничения на тексты: как в основном, так и во вспомогательных текстах, слова разделены в точности одним пробелом.
е) Для разделения слов в тексте используются одиночные символы ″⊔″, ″↑″, ″↓″. Символы ″↑″ и ″↓″ используются в тексте только как корректурные знаки перестановки слов: каждое слово, после которого расположен символ ″↑″, необходимо переместить на место первого позже встречающегося в тексте вхождения символа ″↓″; при этом перемещаемое слово обрамляется с обеих сторон пробелами. Осуществить коррекцию текста. Ограничение на текст: считать, что символы ″↑″ и ″↓″ встречаются только в следующем порядке: ″↑″, ″↓″, ″↑″, ″↓″,...; кроме символов ″⊔″, ″↑″, ″↓″, в тексте используются только латинские (русские) буквы.
5. (Лексикографический порядок.) Сравнить два заданных слова в латинском ( русском) алфавите и установить какое из них в словаре должно предшествовать другому.
Поясняющий пример: в русского словаре
″арка″<″аркан″<″книга″<″том″<″тополь″<″топот″,
где
 означает, что слово
означает, что слово предшествует слову
предшествует слову .
.
Замечание. В алфавите данных широко распространённых языков программирования порядок букв латинского алфавита согласован с естественным, однако порядок букв русского алфавита не согласован. Поэтому ″А″<″В″<″С″..., но обычно ″Ж″ не меньше ″Ф″. Некоторые неудобства может доставить тот факт, что ″Z″<″⊔″.
6.
(Упаковка
повторений.) В
упакованном представлении буквенного
текста вхождение символа –
цифры ″ ″
означает
″
означает -кратное
повторение следующей за ним буквы.
Например текст ″3вс9а2а″
интерпретируется как ″вввсааааааааааа″.
-кратное
повторение следующей за ним буквы.
Например текст ″3вс9а2а″
интерпретируется как ″вввсааааааааааа″.
а) Преобразовать исходный текст, не содержащий символов-цифр, в упакованное представление.
б) Выполнить обратное преобразование, считая, что в упакованном тексте символы-цифры рядом не встречаются.
7. (Сопоставление.)
а) Эталон для сравнения, кроме обычных символов, может содержать специально интерпретируемые символы ″∗″ и ″&″. Вхождение ″∗″ в эталон заменяет произвольный символ на своём месте, вхождение ″&″ − произвольную строку. Сопоставить исходный текст, не содержащий символов ″∗″ и ″&″, с текстом − эталоном.
Поясняющий пример: с эталоном ″s∗n&(&)″ отождествляются тексты ″syn(x)″, ″sine(a+b)″, но не отождествляются текcты ″sin(x)+″, ″arcsin(x)″.
Замечание. Возможны два варианта уточнения задачи 7 а. В первом варианте предполагается, что строка, сопоставляемая символу ″&″, не должна содержать символа, который на эталоне следует за ″&″. Во втором варианте это ограничение отсутствует. Например, текст ″sin(x)+(y)″ отождествляется с эталоном ″s∗n&(&)″ во втором варианте, Второй вариант задачи существенно легче первого.
б) Эталон для сопоставления может содержать только следующие символы: ″х″, ″а″, ″9″, ″.″, ″с″. Интерпретация символов дана в следующей таблице:
|
Символ |
Сопоставляемый символ в исходном тексте |
|
″Х″ |
любой символ |
|
″А″ |
цифра, буква латинского алфавита, пробел |
|
″9″ |
цифра |
|
″.″ |
точка |
|
″С″ |
″+″ или ″-″ или ничего |
Сопоставить исходный текст с текстом -эталоном.
8. (Поиск вхождения.)
а)
Текст-образец
 входит в текст
входит в текст ,
если существует такое число
,
если существует такое число
 ),
что
),
что
 =
= ,...,
,...,
 =
= .
Установить имеется ли вхождение
текста-образца в исходный текст; вычислить
.
Установить имеется ли вхождение
текста-образца в исходный текст; вычислить
 −
номер позиции, с которой начинается
найденное вхождение.
−
номер позиции, с которой начинается
найденное вхождение.
б) Решить задачу, аналогичную предыдущей но при сопоставлении текста – образца с частью исходного текста использовать правила отождествления из задачи 7 а. Дополнительно вычислить номер позиции, в которой заканчивается найденное вхождение.
в)
Текст -образец
 входит в текст
входит в текст ,
если существуют такие
,
если существуют такие ,...,
,..., ,
что
,
что <…<
<…<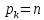 и
и
 =
= ,...,
,...,
 =
= .
Установить, имеется ли вхождение
текста-образца в исходный текст ;
вычислить номера позиций найденного
вхождения.
.
Установить, имеется ли вхождение
текста-образца в исходный текст ;
вычислить номера позиций найденного
вхождения.
9. (Редактировать строки текста. )
а)
Преобразовать заданный текст
 −
последовательность символов
−
последовательность символов
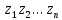 −
в выходной текст, осуществляя замену
символов
−
в выходной текст, осуществляя замену
символов
 (обычно встречающийся в
(обычно встречающийся в )
на
)
на .
Просмотр текста
.
Просмотр текста начинается с первой позиции. Если
обнаружено, что
начинается с первой позиции. Если
обнаружено, что (
( )
совпадает с
)
совпадает с ,
то
,
то заменяется на
заменяется на ,
в результате чего получается текст
,
в результате чего получается текст

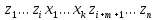 .
.
Просмотр
продолжается с
 -ой
позиции, т.е. с символа
-ой
позиции, т.е. с символа и т.д.
и т.д.
б)
Решить задачу а),
считая последовательность
 закольцованной. Просмотр
начать с заданной позиции.
закольцованной. Просмотр
начать с заданной позиции.
10.
(Задача
Мальвины. ) Пусть
 −
некоторое множество символов. Текст,
читаемый одинаково туда и обратно после
удаления из него символов, входящих в
−
некоторое множество символов. Текст,
читаемый одинаково туда и обратно после
удаления из него символов, входящих в
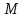 ,
назовём
,
назовём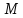 -перевёртышем.
Установить, является ли заданный текст
-перевёртышем.
Установить, является ли заданный текст
 -перевёртышем.
-перевёртышем.
Пример
 -перевёртыша
для {″⊔″}:
-перевёртыша
для {″⊔″}:
″А⊔РОЗА⊔УПАЛА⊔НА⊔ЛАПУ⊔АЗОРА″.
11. (Количество гласных в словах. Использование множества гласных букв.) Для заданного текста подсчитать отдельно количество слов с одной, двумя, тремя и четырьмя гласными. Ограничения на текст те же, что и в задаче 2 г.
12. (Частота букв в тексте. Использование множества букв. ) Вычислить частоты букв во входном тексте.
Пояснение.
Для каждой из букв
 требуется вычислить значения
требуется вычислить значения ,
где
,
где
 −
число вхождений в текст буквы
−
число вхождений в текст буквы
 ,
a
,
a
 −
общее количество букв в
тексте. Символы входящие в текст, но
отличные от латинских букв, в подсчетах
не участвуют.
−
общее количество букв в
тексте. Символы входящие в текст, но
отличные от латинских букв, в подсчетах
не участвуют.
13. (Распределение слов в тексте по их длине .) Для заданного текста подсчитать количество слов, состоящих из одной буквы, из двух букв и т. д.
14. (Частота буквенных пар.) Вычислить частоты буквенных пар в словах заданного текста.
Пояснение.
Здесь требуется построить таблицу (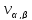 ),
где
),
где −
число появлений сочетания
−
число появлений сочетания
 букв
букв
 и
и
 в словах текста,
в словах текста,
 .
.
15.
(Частотный
словарь текста.) Для
заданного текста напечатать все пары
( ,
,
 ),
где
),
где
 −
слово из текста, а
−
слово из текста, а
 −
число вхождений этого слова в текст.
−
число вхождений этого слова в текст.
Указание.
Реализовать следующий алгоритм. Найдём
в тексте следующее слово
 .
Подсчитаем сколько раз в тексте,
встречается это слово, и напечатаем
соответствующую пару (
.
Подсчитаем сколько раз в тексте,
встречается это слово, и напечатаем
соответствующую пару ( ,
,
 ).
Слова в тексте, совпадающие с
).
Слова в тексте, совпадающие с
 ,
заменим пробелами. Начнём всё с начала,
если в тексте остаётся хотя бы одно
слово.
,
заменим пробелами. Начнём всё с начала,
если в тексте остаётся хотя бы одно
слово.
16.
( Одна из задач
Э. Дейкстры.) Входной
текст образуется из слов, разделённых
одним или несколькими пробелами. Число
букв в слове
 .
В конце текста стоит точка, которая
может быть отделена от последнего слова
несколькими пробелами. Напечатать этот
текст, подвергая его следующим
преобразованиям:
.
В конце текста стоит точка, которая
может быть отделена от последнего слова
несколькими пробелами. Напечатать этот
текст, подвергая его следующим
преобразованиям:
1) ″лишние″ пробелы из текста удаляются;
2) второе, четвертое, шестое и т.д. слова печатаются в обратном порядке.
Поясняющий пример: входной текст
″этот⊔⊔шалаш⊔⊔⊔⊔построил⊔лесник⊔⊔.″
должен быть напечатан в виде:
″этот⊔шалаш⊔построил кинсел.
″
кинсел.
″
Модификация задания: в обратном порядке печатать также слова, состоящие из чётного числа букв.
17.
(Слова
Фиббоначи.) слова
Фиббоначи
 определяются так:
определяются так: ″А″,
″А″,
 ″В″;
″В″;
 для
для .
.
а) Построить первые 11 слов Фиббоначи.
б)
Построить текст
 ∗
∗ ∗…∗
∗…∗ −
последовательность первых 9 слов
Фиббоначи, разделенных символом ″∗″.
−
последовательность первых 9 слов
Фиббоначи, разделенных символом ″∗″.
18.
(Подстановка.)
Перестановка
 (
( ,
, ,
, ,…,
,…, )
букв латинского алфавита определяется
вводом. Преобразовать входной текст в
выходной, заменяя каждую букву
)
букв латинского алфавита определяется
вводом. Преобразовать входной текст в
выходной, заменяя каждую букву входного текста на букву
входного текста на букву в выходном тексте.
Символы, не являющиеся буквами латинского
алфавита оставить без изменения.
в выходном тексте.
Символы, не являющиеся буквами латинского
алфавита оставить без изменения.
19.
(Транспозиция.)
Преобразовать входной текст
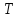 в выходной,выполняя над ним следующие
действия: текст делится на группы
символов длины
в выходной,выполняя над ним следующие
действия: текст делится на группы
символов длины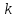 ;
к каждой группе применяется одна и та
же перестановка
;
к каждой группе применяется одна и та
же перестановка .
.
Пояснение.
Перестановку
 можно задать как некоторую перестановку
первых
можно задать как некоторую перестановку
первых натуральных чисел. Так, если
натуральных чисел. Так, если и
и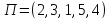 ,
то текст
,
то текст будет преобразован в
будет преобразован в

Длина
текста
 должна быть кратна
должна быть кратна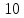 .
Если такого ограничения не вводить, то
лишний ″хвост″текста следует отсечь.
.
Если такого ограничения не вводить, то
лишний ″хвост″текста следует отсечь.
20. (Двоичное преобразование.)
а) Преобразовать входной текст, записанный исключительно русскими буквами (но без буквы ″Ё″) в выходную двоичную последовательность, заменяя букву ″А″ на комбинацию цифр ″00000″, ″Б″ – на ″00001″, ″В″ – на ″00010″, ..., ″Я″– на ″11111″. (Почему буква ″Ё″ удалена из алфавита ?)
б) Выполнить обратное преобразование.
21. (Троичное преобразование.)
а)
Преобразовать входной текст, записанный
латинскими буквами с использованием
символа пробела, в выходной текст в
трехсимвольном алфавите, заменяя каждый
символ (букву или пробел) на соответствующую
комбинацию цифр




б) Выполнить обратное преобразование.
22. (Азбука Морзе.) В радиотелеграфии используют следующую последовательность точек, тире и пробелов:
|
A |
.- ⊔ |
|
J |
.---⊔ |
|
S |
...⊔ |
|
B |
-..⊔ |
|
K |
-.-⊔ |
|
T |
-⊔ |
|
C |
-.-.⊔ |
|
L |
.-..⊔ |
|
U |
..-⊔ |
|
D |
-..⊔ |
|
M |
--⊔ |
|
V |
...-⊔ |
|
E |
.⊔ |
|
N |
-.⊔ |
|
W |
.-- ⊔ |
|
F |
..-.⊔ |
|
O |
---⊔ |
|
X |
-..-⊔ |
|
G |
--.⊔ |
|
P |
.--.⊔ |
|
Y |
-.--⊔ |
|
H |
....⊔ |
|
Q |
--.-⊔ |
|
Z |
--..⊔ |
|
I |
..⊔ |
|
R |
.-.⊔ |
|
|
|
а) Преобразовать входной текст,записанный латинскими буквами с использованием символа пробела,в выходной текст из точек,тире и пробелов.
б) Выполнить обратное действие.
23.
(Перемешивание
текста.) Напечатать
текст, получаемый в результате следующего
перемешивания входного текста. Пусть
 −
некоторый (определяемый
вводом) набор неотрицательных чисел.
Числа, входящие в
−
некоторый (определяемый
вводом) набор неотрицательных чисел.
Числа, входящие в
 ,
выписываются (с повторением) под символами
текста. Далее, если под символом
,
выписываются (с повторением) под символами
текста. Далее, если под символом из текста записано число
из текста записано число ,
то
,
то заменяется на тот символ, который стоит
заменяется на тот символ, который стоит -ым после
-ым после в некотором стандартном расположении
всех символов алфавита по кругу.
в некотором стандартном расположении
всех символов алфавита по кругу.
24.
(Квадрат-решётка.)
Хорошо известен (см., в частности, [1],
с.136, задача 62) следующий способ
перемешивания текста. Возьмем квадрат
размером
 клеток, в котором удалено
клеток, в котором удалено клеток. Через прорези в квадрате,
образовавшиеся в результате удаления
клеток, на бумагу наносятся первые
символы текста. Затем квадрат поворачивается
на
клеток. Через прорези в квадрате,
образовавшиеся в результате удаления
клеток, на бумагу наносятся первые
символы текста. Затем квадрат поворачивается
на по часовой стрелке, и через прорези
записываются следующие символы текста.
Эта процедура повторяется ещё дважды.
После заполнения квадрата первыми
по часовой стрелке, и через прорези
записываются следующие символы текста.
Эта процедура повторяется ещё дважды.
После заполнения квадрата первыми символами текста его строки последовательно
выписываются друг за другом. В результате
будет получен перемешанный текст.
символами текста его строки последовательно
выписываются друг за другом. В результате
будет получен перемешанный текст.
а) Для заданного квадрата-решётки перемешать входной текст описанным выше способом.
б) Выполнить обратное преобразование.
Замечание.
Каждый квадрат-решетка должен обладать
свойством: из любых четырех клеток ( ),
(
),
( ),
(
),
(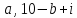 )
и (
)
и ( i),
где
i),
где
 ,
удалена только одна. Лишь в этом случае
ни один символ не будет записан на месте
другого и квадрат будет полностью
заполнен.
,
удалена только одна. Лишь в этом случае
ни один символ не будет записан на месте
другого и квадрат будет полностью
заполнен.
