Ряд Тейлора

В первой части курса для раз дифференцируемой функции была получена формула Тейлора

,

и ее частный случай – формула Маклорена

.

Вопрос ставится так, нельзя ли обобщить формулу Тейлора для бесконечно дифференцируемой функции, представив ее в виде ряда.

Поскольку формула Тейлора превращается в формулу Маклорена при помощи замены , не нарушая общности рассуждений, рассмотрим такую возможность для формулы Маклорена.

Пусть

,

тогда - основная часть формулы Маклорена - является одновременно частичной суммой степенного ряда. В соответствии с формулой Маклорена

,

то есть остаток в формуле Маклорена должен являться остатком степенного ряда. Но предел остатка ряда придолжен стремиться к нулю, что следует из теории рядов. Таким образом, представлениевозможно при выполнении условияи, конечно, в области сходимости степенного ряда.

Имеются различные формы представления остатка в формуле Маклорена. Представим остаток в форме Лагранжа ,

где . Проведем его оценку абсолютной величины остатка, для чего с помощью признака Даламбера исследуем сходимость ряда:при любом конечном значении. Но для сходящегося ряда должно выполняться необходимое условие сходимости, то есть прии любом конечном значениикак, так истремятся к нулю. Значит, прибесконечно малая функция. Если функция- ограничена, то также бесконечно малая, следовательно,

.

Разложение в ряд функции

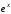
В первой части курса математического анализа была получена формула Маклорена для этой функции. Приведем эту формулу, приняв остаточный член в форме Лагранжа

,

Рассмотрим остаток ряда . Как уже говорилось выше, первый сомножитель в этом выражении прии любом конечном значении– есть бесконечно малая функция. Но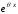также при любом значении- ограниченная величина:. Известно, что бесконечно малая, умноженная на ограниченную функцию, также является бесконечно малой и, следовательно,, конечно, в области сходимости ряда. Определим радиус сходимости ряда. Поскольку,. Тогда. Область сходимости ряда для функции, следовательно,.

Эта область фактически уже определена выше с помощью признака Даламбера, в результате применения которого установлено, что предел при любом равен нулю, и ряд сходится абсолютно при любом.

Разложение с помощью МАКСИМЫ

D формуле Тейлора первым параметром является разлагаемая функция, второй указывает, по какой переменной происходит разложение, третий – в окрестности какой точки это разложение (в ряде Маклорена), последний аргумент задает количество членов разложениия

Представление в виде рядов функций .

Запишем формулы Маклорена для функций и. И представим остаточные члены в форме Лагранжа. Пусть. Тогда

, ,,.

Покажем, что я производная вычисляется по формуле. В самом деле, приимеем, приполучаем, при, очевидно,, приимеем,

при и так далее. Нетрудно заметить, что формула дляой производной верна. Отсюда следует, что прифункция равна 1, все ее нечетные производные равны нулю, а четные равны. Формула Маклорена принимает вид

,

().

Докажем, что я производная функцииможет быть представлена формулой.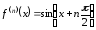

Проверим это. ,,,и так далее.

Из формулы для ой производной имеем прифункцияи ее четные производные равны нулю, а нечетные. Итак,

.

Поскольку

, ,,

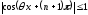имеем

,  .

Таким образом,

,

. .

Поскольку остаточные члены обоих рядов стремятся к нулю при , областью сходимости обоих рядов является вся числовая ось.

Проверим этот результат, для чего исследуем ряды из абсолютных величин

, .

В соответствии с признаком Даламбера

,

пределы в обоих случаях равны 0 при любых , и в соответствии с признаком Даламбера область сходимости рядов дляи, действительно,.

Разложение в МАКСИМЕ

Разложение в ряд функции

Используем геометрическую прогрессию, рассмотренную в начале темы "Ряды"

,

Она сходится, если . Пригеометрическая прогрессия представляет собой степенной ряд

,

сходящийся, естественно, в области . Его сумма была определена выше, она равна.

Как уже говорилось, степенной ряд можно почленно интегрировать в промежутке его сходимости. Выберем некоторое и вычислим

,

откуда следует

,

или

.

Ряд сходится в той же области , что легко проверяется.

В МАКСИМЕ