Степенные ряды

Ряд , гдепостоянные коэффициенты, называется степенным. Очевидно, этот ряд есть частный случай функционального ряда, следовательно, не обязательно сходится при любых. Естественно, представляет интерес определение области сходимости степенного ряда, то есть то множество значений аргумента, при которых ряд сходится.

Теорема. Степенной ряд 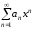сходится абсолютно в области, где, и расходится в области.

Доказательство. Поскольку , да ине обязательно положительны, ряд, вообще говоря, является знакопеременным. Чтобы доказать абсолютную сходимость ряда, необходимо рассмотреть ряд из абсолютных величин членов этого ряда. Теперь к знакоположительному числовому ряду применим признак Даламбера:, где. В соответствии с признаком Даламбера рассматриваемый ряд сходится прии расходится в области. Итак, область абсолютной сходимости степенного ряда, где. В областиряд расходится.

Вследствие этого, промежуток называется областью абсолютной сходимости степенного ряда, аназывают радиусом его сходимости.

Замечания.

1). Признак Даламбера не работает, если предел равен единице, следовательно, он неприменим при (). Исследование сходимости рядов в этих точках производится отдельно.

2). При выведении формулы радиуса сходимости степенной ряд считался "полным", то есть в нем присутствовали все целые, положительные степени . Если ряд не содержит всех степеней, формула для радиуса сходимости будет неверной. В этом случае при исследовании сходимости каждого конкретного степенного ряда следует составить ряд из модулей его членов, после чего применить признак Даламбера. Очевидно, такую процедуру можно применять и при определении области сходимости и "полных" рядов.

Пример 1.

. Ряд "полный", его можно исследовать двумя способами.

Первый способ.

.

Итак, .

Второй способ. Рассматривается ряд . Пустьобщий член этого ряда, тогда. Применяем признак Даламбера

.

Естественно, получается тот же результат.

Исследуем граничные значения области сходимости.

При получаем числовой ряд. Ряд знакоположительный, его члены меньше членов сходящегося ряда, следовательно, он сходится.

При имеем знакочередующийся числовой ряд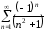. Рассмотрим ряд из модулей его членов, но это сходящийся ряд, что мы только что подтвердили, следовательно, знакочередующийся ряд сходится абсолютно. Итак, область абсолютной сходимости исследуемого ряда. При остальных значенияхряд расходится.

Пример 2. Ряд "неполный", так как содержит только нечетные степени. Применяем второй способ, рассмотрев ряд из абсолютных величин членов исходного ряда. Применим к нему признак Даламбера. Общий член ряда, тогда. Подсчитаем предел

.

Получаем область сходимости или.

Исследуем граничные точки:

при имеем. Знакоположительный рядрасходится, что следует из сравнения его с расходящимся рядомс помощью второй теоремы сравнения. Предел отношения членов этих рядов. Поскольку значение предела больше нуля и меньше бесконечности, ряды ведут себя одинаково. Очевидно, расходится и получившийся на границе знакоотрицательный ряд;

при имеем. Это знакочередующийся ряд, он сходится условно, так как.

Итак, область сходимости ряда .

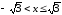Свойства степенных рядов

1. Сумма степенного ряда в области (промежутке) его сходимости есть непрерывная функция.

2. Степенной ряд в его области (промежутке) сходимости можно почленно интегрировать, причем сумма нового ряда равна интегралу от суммы исходного ряда.

3. Степенной ряд в промежутке его сходимости можно почленно дифференцировать, сумма продифференцированного ряда равна производной суммы исходного ряда.

Примечание. Часто встречаются степенные ряды, более общего вида

.

При исследовании их области сходимости делается замена , приводящая ряд к уже известному ряду.

Исследование степенных рядов с помощью МАКСИМЫ

Рассмотрим изученный выше ряд

Итак, радиус сходимости 1. В граничных точках области ряды сходятся в соответствии с третьей командой. Область сходимости ряда .

Примеры для самостоятельного решения

Исследовать сходимость степенных рядов

16.1. , 16.2., 16.3., 16.4.,

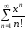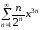16.5. , 16.6., 16.7., 16.8..

Ответы.

16.1. , 16.2., 16.3., 16.4.,

16.5. , 16.6., 16.7., 16.8..