Функциональные ряды

Если числовые ряды в настоящее время используются, в основном для отработки методики исследования их сходимости, то функциональные ряды имеют широчайшее применение при решении различных уравнений, особенно в случаях, когда их точное решение построить не удается. Более того, решение уравнения в виде ряда считается точным, если сходимость ряда доказана. Не менее успешно используются функциональные ряды при вычислении приближенных значений некоторых функций. Точное значение даже такой простой функции, как , известно только для нескольких значений аргумента (и так далее). Чтобы подсчитать значение этой функции в промежуточных точках, используется представлениев виде ряда. Кстати, при вычислении этой функции с помощью компьютера или микрокалькулятора фактически используется ее "разложение в ряд".

Широкую известность получили степенные ряды, ряд Фурье и различные его модификации.

Общая теория функциональных рядов

Теория функциональных рядов общего вида является обобщением теории числовых рядов. Многие положения из числовых рядов с определенными оговорками переносятся на функциональные ряды.

Дан функциональный ряд . По аналогии с числовыми рядами введем понятиечастичной суммы ряда

и его остатка .

Справедливой остается теорема, что из сходимости ряда следует сходимость его остатка и наоборот. Если ряд расходится, то расходится и его остаток, а из расходимости остатка следует расходимость ряда. Более того, если ряд сходится, то есть имеет конечную сумму , то. В самом деле,, но, откуда следует

.

Сходимость, равномерная сходимость ряда

Рассмотрим сходимость и равномерную сходимость остатка ряда , что несколько проще, но приводит к тому же результату. Используем для этого теорию числовых рядов. Пусть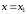, тогдаесть числовой ряд. Он может сходиться или расходиться. Пусть этот ряд сходящийся, тогда

.

Пусть при числовой рядтакже сходится, тогда

.

Нетрудно понять, что один из этих рядов может сходиться медленнее, чем другой, следовательно, ине обязательно равны, то есть.

В результате, если остаток ряда сходится в некоторой области, то

,

отсюда следует, что при сходимости ряда в некоторой области для всех из этой области выполняется условие

Для некоторых рядов удается определить область, где выполняется условие

,

то есть значение одинаково для всех точек рассматриваемой области. В этом случае ряд называется равномерно сходящимся в этой области.

Покажем на примере, что некоторые ряды являются равномерно сходящимися, но есть и такие сходящиеся ряды, которые не сходятся равномерно.

Пример 1. Рассмотрим ряд

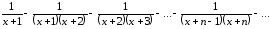
в области , гделюбое положительное число.

Легко установить, что данный ряд можно представить в виде

Подсчитаем ю частичную сумму ряда, предварительно раскрыв скобки, очевидно,. Определим сумму ряда. Поскольку, имеем, а.

Но в этом случае

,

откуда следует, что и, посколькуиположительные числа, то

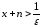, откуда имеем . Итак, установлено, начиная с которого выполняется условие сходимости остатка ряда. Следовательно, ряд в областисходится.

Если мы выберем , топри любыхиз заданной области, следовательно, условие

выполняется при любом , ине зависит от. Ряд в указанной области сходится равномерно.

Пример 2. Рассмотрим ряд

в области . Запишем, предварительно раскрыв скобки и произведя сокращения. Тогда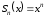. Сумма ряда в указанной области. Остаток ряда, причем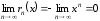. Определим, начиная с которого выполняется условие. Очевидно, в заданной области изследует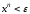. Логарифмируя, получаем. Поскольку в рассматриваемой области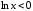,. Итак,. При этом невозможно найти такое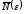, не зависящее, чтобы выполнялось условие равномерной сходимости. Дело в том, что при, то есть с ростомчислорастет до сколь угодно больших величин. Отметим, что прине равным нулю остается только первый член. Итак, в областиряд сходится, но не равномерно.

Свойства равномерно сходящихся рядов

1. Если члены ряда - есть непрерывные в некоторой областифункции, а ряд в этой области сходится равномерно, то сумма ряда - непрерывная в этой области функция.

2. Если члены ряда непрерывные в области функции и ряд сходится в ней равномерно, то его можно почленно интегрировать в любых пределах, лежащих в указанном промежутке, причем

.

3. Если ряд сходится в промежутке, и его члены имеют непрерывные в этом промежутке производные, причем ряд из производныхсходится вравномерно, то рядтакже сходится равномерно, и его можно дифференцировать почленно, причем

.