dm_bilety (1)

На каждом такте выполняется одна команда. Пусть в некоторый момент времени t УУ находится в состоянии q_i, а головка обозревает ячейку, в которой записан символ a_j, тогда выполняется q_ia_j … .

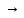Замечание. В программе не должно быть двух разных команд с одной и той же первой частью.

Выполнение команды заключается в том, что символ a_j стирается и на его место записывается a_l; головка сбивается на одну ячейку влево или вправо, либо остается на месте в зависимости от 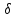; и к моменту времени t+1 УУ переходит в состоянии q_r функционирование М прекращается, когда УУ перейдет в стоп-состояние (q₀).

Машина Тьюринга M вычисляет словарную функцию

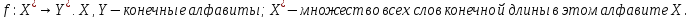
Берем x=x₁,x₂, …,x_n ϵ X*.

Пусть f(x)=y₁,y₂, …y_p , тогда M должна, начиная со стандартной начальной конфигурации со словом Х, перейти в заключительную стандартную конфигурацию со словом У.

Если f(x) не определена, то М не должна останавливаться.

Т.е. было

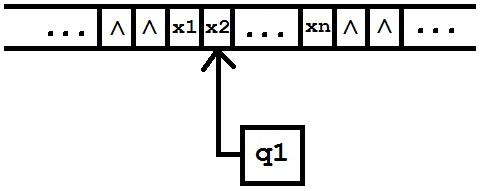
стало:

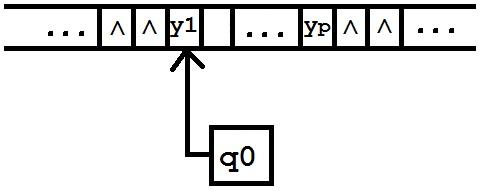
Т.

1) Говорят, что словарная функция 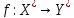вычислима по Тьюрингу, если существует машина Тьюринга, вычисляющая эту функцию (мы работаем не с числами, а с их изображением).

2) А – конечный алфавит, что связано с ограничением на выпускающую (разрешающую) способность.

3) Q – конечное (количество состояний).

БИЛЕТ 52

Примеры построения машин Тьюринга

Таблица управления машиной Тьюринга – распознавание симметрии.

qi\aj	0	1	˄	коммент.
q1	˄Rq2	˄Rq3	1Sq0
q20	0Rq2	1Rq2	˄Lq4
q3
q4	˄Lq5	˄Lq6	1Sq0
q5	0Lq5	1Lq5	˄Rq1
q6	˄Lq6	˄Lq6	0Sq0
q7	^Lq6	˄Lq5	1Sq0

БИЛЕТ 53

Функции, вычислимые по Тьюрингу.  Пусть  =(₁, ..., _n), n1- произвольный набор целых неотрицательных чисел. Слово 1^1+101^2+10...01^n+1 называется основным машинным кодом или просто кодом набора  в алфавите {0,1} и обозначается k(). Слово 1^+1 также является основным машинным кодом. Для ясности 1³ это 111. Определение. Функция f(x₁,...,x_n), n1, называется частичной числовой функцией, если переменные x_i принимают целые неотрицательные значения из натурального ряда N={0,1,2,…,m,…} и на наборе  функция определена, т.е. f()=f(₁,...,_n), и также принимаeт целые неотрицательные значения. Определение. Частичная числовая функция называется вычислимой по Тьюрингу, если существует МТ Т_f, обладающая следующими свойствами:  1) если функция f() определена, то результатом применения МТ к коду будет являться код целого неотрицательного числа. Т_f(k())=k(f()) 2) если f() не определенна, то либо МТ T_f не применима к слову k(), либо T_f(k()) не является кодом никакого целого неотрицательного числа. Предполагается, что в начальный момент времени головка МТ T_f обозревает самую левую крайнюю единицу слова k(). Если функция f вычислима по Тьюрингу с помощью МТ T_f , то говорят, что МТ вычисляет функцию. Кроме того, т.к. понятие вычислимой функции дано нами через понятие МТ, которое еще математически точно не определено, будем говорить об интуитивно вычисляемой функции. ^ Тезис Тьюринга: Всякий интуитивный алгоритм может быть реализован с помощью МТ. Тезис Черча-Тьюринга: Всякая интуитивно вычисляемая функция вычислима по Тьюрингу. ^ МТ как математическое понятие алгоритма. В каждой МТ имеются: три конечных множества A, Q, T, выделенные элементы a₀A, q₀,q₁Q и программа, представляющая собой отображение вида F: AQ\{q₀}A TQ. (7.3) Определение. МТ называется система вида 0, Q, q0, q1, T, >, где  - программа МТ. Какую бы МТ ни взяли, можно считать, что имеется алгоритм, исходным объектом, промежуточным и окончательным результатами которого являются слова в алфавите А. Предписанием, задающим этот алгоритм, является программа  - точное математическое понятие отображения. Т.о., с математической точки зрения МТ - это алгоритм переработки слов, заданных в алфавите этой машины. Применительно к МТ можно рассматривать все свойства, рассматриваемые применительно к интуитивному понятию алгоритма. В частности, результативность алгоритма и его конечность - это остановится ли МТ за конечное число тактов работы и в какое слово перерабатывается исходное. Чтобы доказать, что функция вычислима по Тьюрингу, необходимо построить МТ, вычисляющую данную функцию. Пример: 1) Построить МТ, вычисляющую функцию f(x,y)=x+y. В качестве внешнего алфавита возьмем  A={a0, 1} , где a0- пустой символ. Тогда в этом алфавите 0 - 1 1 - 11  2 – 111

3 - 1111, и т.д. Q={q0,q1,q2,q3,q4} X и Y будут записаны на ленте и разделены одной ячейкой, содержащей пустой символ. МТ обозревает самую левую крайнюю непустую ячейку. Программа, вычисляющая данную функцию будет иметь вид:  1q11Пq1

a0 q11Пq2 1q21Пq2 a0q2 a0Лq3 1q3 a0Лq4 1q4 a0Лq0  Можно показать, что все арифметические функции вычислимы по Тьюрингу.

БИЛЕТ 54

Тезис Тьюринга-Чёрча.

Класс функций, вычислимых алгоритмически (в интуитивном смысле слова), совпадает с классом функций вычислимых по Тьюрингу.

Доводы:

1. Все формализации понятия алгоритма и алгоритмически вычислимой функции оказались равнообъемными.

Примеры формализации: частично рекурсивные функции Чёрча, машины Комогорова-Успенского (мощнее машины Тьюринга), программы на алгоритмическом языке (Pascal).

2. Любая функция по Тьюрингу является алгоритмически вычислимой.

3. Все функции, которые признавались алгоритмически вычислимыми, оказались вычислимыми по Тьюрингу.

4. Деятельность тысяч программистов.