1.1. Линейная модель парной регрессии и корреляции

Рассмотрим простейшую модель парной регрессии – линейную регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду явной экономической интерпретации ее параметров.

Линейная регрессия имеет теоретическое уравнение вида:

. (1.1)

Уравнение вида 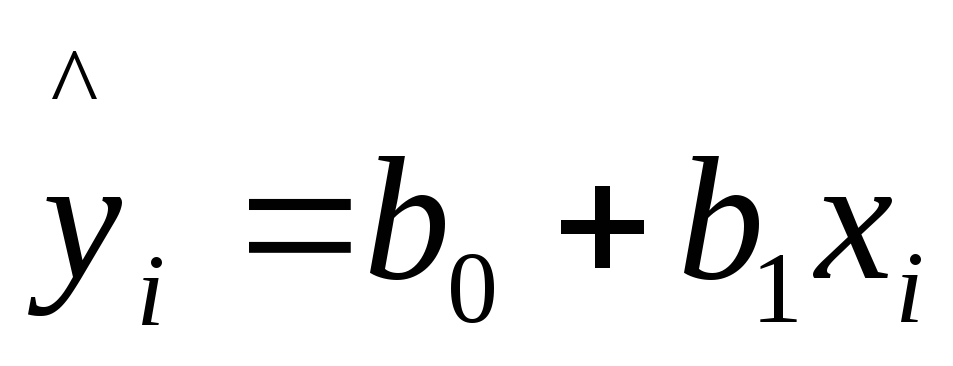позволяет по заданным значениям факторанаходить теоретические значения результативного признака, подставляя в него фактические значения фактора.

Построение линейной регрессии сводится к оценке ее параметров – b₀ и b₁. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров b₀ и b₁, при которых сумма квадратов отклонений фактических значений результативного признака от теоретическихминимальна:

. (1.2)

Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):

Рис. 1.2. Линия регрессии с минимальной дисперсией остатков

Как известно из курса математического анализа, чтобы найти минимум функции (1.2), надо вычислить частные производные по каждому из параметров b₀ и b₁ и приравнять их к нулю. Обозначим через , тогда:

.

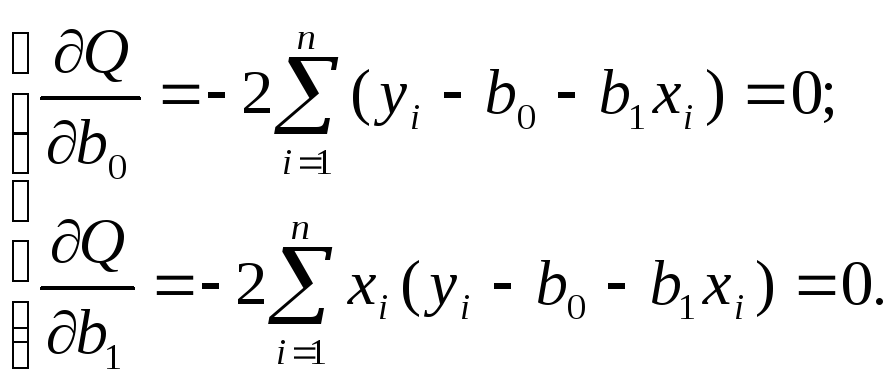(1.3)

После несложных преобразований получим следующую систему линейных уравнений для оценки параметров b₀ и b₁:

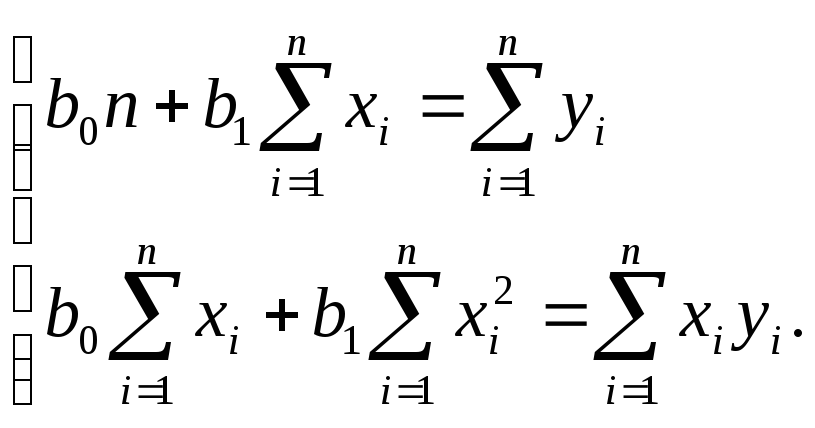(1.4)

Решая систему уравнений (1.4), найдем искомые оценки параметров b₀ и b₁. Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (1.4):

,

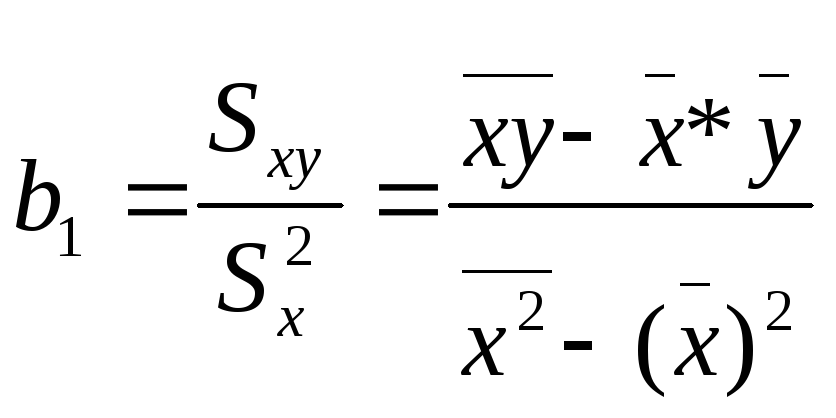, (1.5)

где ; ; ;

–ковариация признаков и, – дисперсия признака .

Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий.

Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.

Параметр b­₁ называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

Формально b₀ – значение при. Если признак-факторне может иметь нулевого значения, то вышеуказанная трактовка свободного членаb₀ не имеет смысла, т.е. параметр b₀ может не иметь экономического содержания.

1.2. Нелинейные модели регрессии и их линеаризация

При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются по МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию

,

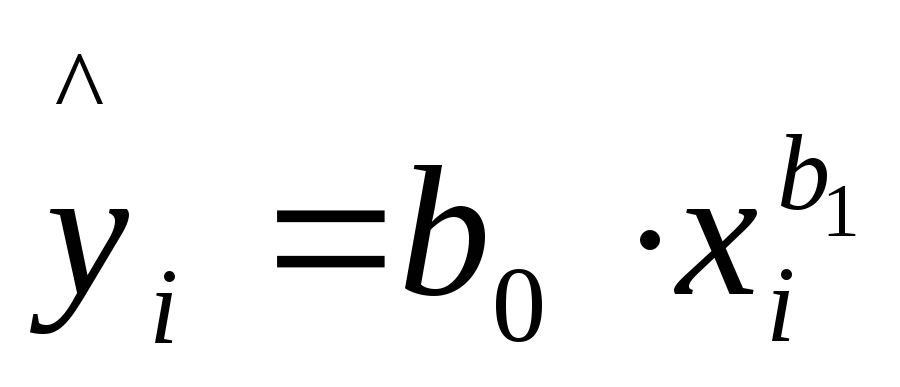мы преобразовываем ее в линейный вид:

,

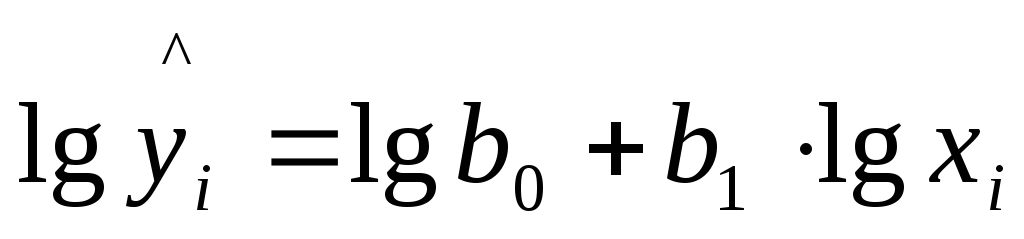где переменные выражены в логарифмах.

Далее обработка МНК та же: строится система нормальных уравнений и определяются неизвестные параметры. Потенцируя значение , находим параметрb₀ и соответственно общий вид уравнения степенной функции.

Вообще говоря, нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Эта оценка определяется, как и в линейной регрессии, МНК, рассмотренным выше.

.
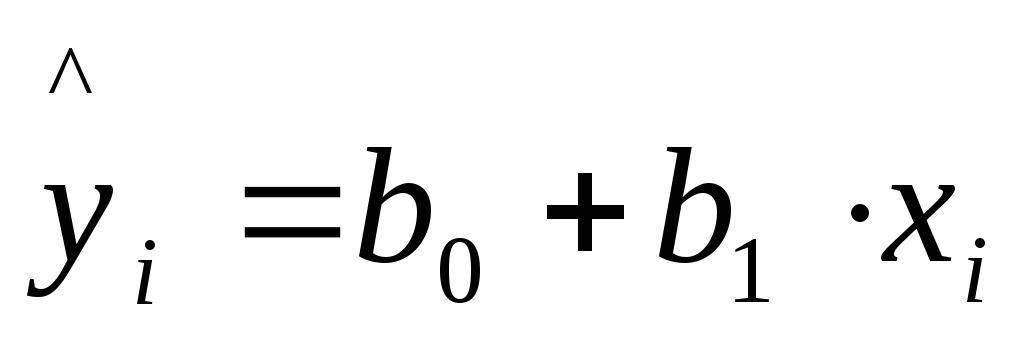