3.1. Решение типовых задач

На примере задачи 2.6.1 рассмотрим обозначенные выше способы обнаружения автокорреляции остатков.

1. Критерий Дарбина-Уотсона.

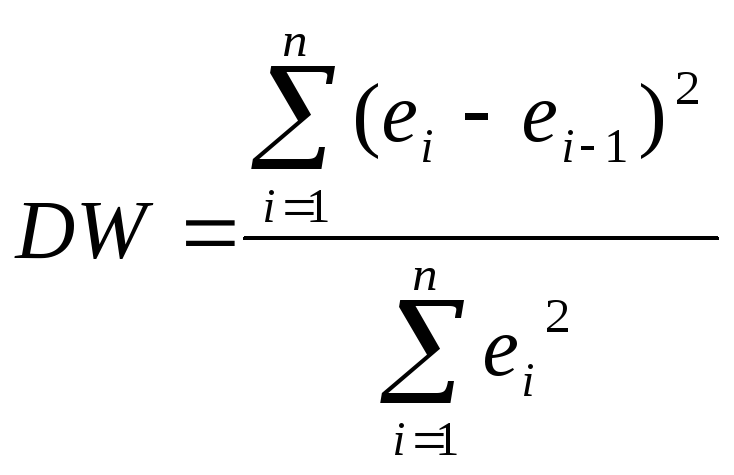
Для расчета данной статистики необходимо рассчитать две суммы: и. Значения этих сумм можно получить используя расчетную таблицу (см. выше задача 2.6.1). В данном случае= 21343,64, а= 15453,08, следовательно:

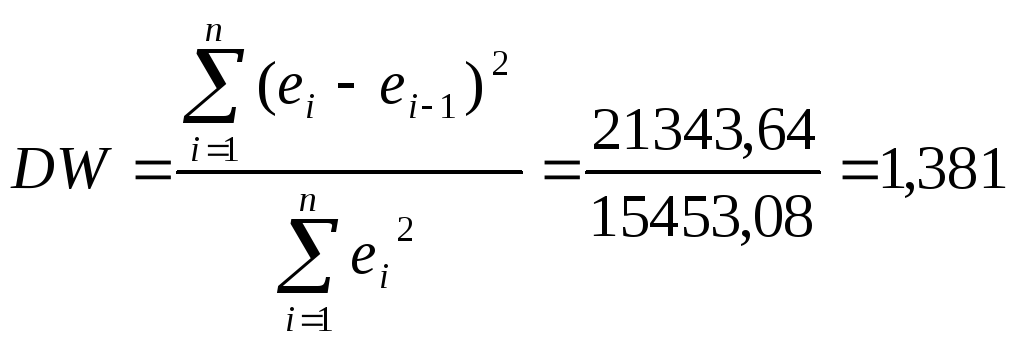
По таблице критических точек Дарбина-Уотсона определяются два числа d_L и d_U и осуществляют вывод по следующей схеме:

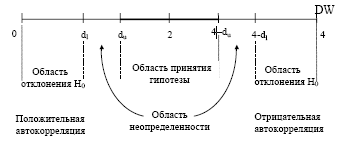
В данном случае d_L = 0,697, d_U = 1,641. Обозначим, полученные значения на отрезке.

0,697

0,697

1,641

2,359

3,303

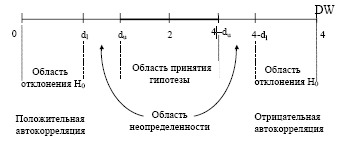
Так как статистика DW = 1,381 попадает в область неопределенности, то нельзя с полной уверенностью сделать вывод о поведении отклонений e_i. Необходимо воспользоваться другим методом обнаружения автокорреляции остатков, например, методом рядов.

2. Метод рядов.

Последовательно определяются знаки отклонений e_i. В данном случае,

(+)(-----)(+++)(-),

n (объем выборки) = 10;

n₁ (общее количество знаков «+» при n наблюдениях) = 4;

n₂ (общее количество знаков «-» при n наблюдениях) = 6;

k (количество рядов) = 4.

По таблицам критических значений количества рядов для определения наличия автокорреляции по методу рядов на пересечении строки n₁ и столбца n₂ определяется нижнее k₁ и верхнее k₂ значения при уровне значимости  = 0,05. В данном случае k₁ = 2, верхнее k₂ = 9. Следовательно, если k₁ < k < k₂, то делаем вывод об отсутствии автокорреляции.

В случае обнаружения автокорреляции в модели, необходимо ее устранить одним из следующих методов:

1. авторегрессионная схема первого AR(1), второго порядка AR(2), третьего AR(3) порядка;

2. метод Кохрана-Оркатта;

3. метод Хилдрета-Лу

4. метод первых разностей.

3.2. Упражнения и задачи

Задача 3.2.1.

По данным задачи 2.7.7. (см. выше) определить наличие в модели автокорреляции остатков, используя статистику Дарбина-Уотсона и метод рядов.

Задача 3.2.2.

Определить наличие автокорреляции методом рядов и проверить ее присутствие с помощью статистики Дарбина-Уотсона.

ei

8,3

4,26

-12,46

-1,86

-7,38

5,26

-9,66

-2,26

8,34

7,46

4. Гетероскедастичность

4.1. Суть гетероскедастичности

Одной из предпосылок МНК является условие постоянства дисперсий случайных отклонений (гомоскедастичность). Не должно быть априорной причины, вызывающей большую ошибку (отклонение) при одних наблюдениях и меньшую — при других. Невыполнимость данной предпосылки называется гетероскедастичностью.

На практике гетероскедастичность не так уж и редка. Проблема гетероскедастичности характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов. Оценки, полученные по МНК, при наличии гетероскедастичности не будут эффективными (то есть они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Стандартные ошибки коэффициентов будут занижены. Поэтому статистикибудут завышены, что может привести к признанию статистически значимыми коэффициентов, которые таковыми не являются. Доверительные интервалытеоретических коэффициентов уравнения линейной регрессии получаются уже, чем на самом деле.

Как выяснить наличие гетероскедастичности и смягчить ее по следствия?