
- •1. Теория информации
- •1.1 Теорема Котельникова
- •1.2 Квантование сигнала по уровню
- •2. Мера информации
- •2.1 Мера информации по Шеннону
- •2.2 Энтропия дискретного ансамбля сообщений
- •2.3 Энтропия непрерывного ансамбля сообщений
- •2.4 Энтропия непрерывного ограниченного ансамбля
- •2.3 Количество взаимной информации
- •2.3.1 Дискретный канал передачи информации
- •2.3.2 Непрерывный канал передачи информации
- •2.3.3 Эпсилон-энтропия (ε-энтропия)
- •Кодирование источника информации
- •3.1 Метод кодирования равномерным кодом
- •3.2 Метод кодирования Шеннона-Фано
- •3.3 Метод кодирования Хафмана
- •3.4 Теорема оптимального кодирования источника независимых сообщений.
- •4 Канал связи
- •4.1 Скорость передачи информации и пропускная способность канала связи
- •4.2 Канал без шумов
- •4.3 Канал с шумами
- •4.4 Непрерывный канал связи
- •4.5 Теорема Шеннона о пропускной способности частотно ограниченного канала
- •5. Кодирование в канале
- •5.1 Систематические коды
- •5.1.1 Образование систематического кода
- •5.1.2 Систематический код Хемминга
- •5.2 Циклические коды
- •5.2.1 Обнаружение однократной ошибки
- •5.2.2 Исправление однократной ошибки
- •1. Теория информации 1
5.2 Циклические коды
Циклические коды являются разновидностью систематических кодов. Они получили широкое распространение из-за простоты кодирования и декодирования. Все разрешённые кодовые комбинации производящей матрицы могут быть получены циклическим сдвигом одной разрешённой комбинации, называемой образующей для данного кода.
Любой
![]() -разрядный
код можно представить в виде полинома
степени
-разрядный
код можно представить в виде полинома
степени![]()
![]() ,
,
где
![]() - основание счисления,
- основание счисления,
![]() - коэффициенты, принимающие значения
«0» или «1», если
- коэффициенты, принимающие значения
«0» или «1», если![]() .
.
Например, комбинацию 110101 можно записать как
![]() .
.
Циклический сдвиг эквивалентен умножению
многочлена
![]() на
на![]() .
.
Действительно,
![]() .
.
Но в кодовой комбинации должно быть
всего
![]() членов, причём степень полинома не
должна превышать
членов, причём степень полинома не
должна превышать![]() .
Чтобы удовлетворить этому условию,
положим
.
Чтобы удовлетворить этому условию,
положим![]() .
Тогда получим
.
Тогда получим
![]() ,
,
т.е. получили циклический сдвиг. Если
код, выраженный в виде полинома,
принадлежит разрешённой кодовой
комбинации, то кодовая комбинация,
полученная циклическим сдвигом, также
принадлежит разрешённой кодовой
комбинации. Из условия того, что
![]() имеем
имеем
![]() .
(5.16)
.
(5.16)
Пусть имеется полином
![]() степени
степени![]() .
Среди полиномов
.
Среди полиномов![]() выделим полиномы, которые делятся только
лишь на самого себя и на 1. Такие полиномы
называются простыми или неприводимыми.
выделим полиномы, которые делятся только
лишь на самого себя и на 1. Такие полиномы
называются простыми или неприводимыми.
Рассмотрим неприводимый полином
![]() и различные кодовые комбинации, выраженные
в виде полиномов
и различные кодовые комбинации, выраженные
в виде полиномов![]() степени
степени![]() .
Из всей совокупности полиномов
.
Из всей совокупности полиномов![]() к числу разрешённых кодовых комбинаций
отнесём только те, которые делятся без
остатка на полином
к числу разрешённых кодовых комбинаций
отнесём только те, которые делятся без
остатка на полином![]() .
Определённый таким образом полином
.
Определённый таким образом полином![]() степени
степени![]() называется образующим.
называется образующим.
Циклическими
![]() кодами называются коды, каждая кодовая
комбинация которых, выраженная в виде
полинома, имеет степень, не превышающую
кодами называются коды, каждая кодовая
комбинация которых, выраженная в виде
полинома, имеет степень, не превышающую![]() ,
и нацело делится на образующий полином
,
и нацело делится на образующий полином![]() степени
степени![]() .
.
Ввиду того, что циклические коды относятся к группе систематических кодов, то можно построить производящую матрицу.
Каноническая форма производящей матрицы
![]() размерности
размерности![]() (5.10) состоит из зеркального отражения
единичной подматрицы размерности
(5.10) состоит из зеркального отражения
единичной подматрицы размерности![]() ,
( матрица отражения [Марпл]),
и проверочной подматрицы размерности
,
( матрица отражения [Марпл]),
и проверочной подматрицы размерности![]() .
.
 .
(5.23)
.
(5.23)
Каждую строку матрицы
![]() разделим
на неприводимый полином
разделим
на неприводимый полином![]() ,
дающийnостатков, и
заменим нули в соответствующей строке
проверочной части матрицы на остаток
,
дающийnостатков, и
заменим нули в соответствующей строке
проверочной части матрицы на остаток![]() .
Результирующая матрица
.
Результирующая матрица![]() будет производящей матрицей циклического
кода
будет производящей матрицей циклического
кода![]() .
.
Пример 5.5. Пустьn= 7,k= 4,r= 3. Первоначальное значение производящей матрицы имеет вид
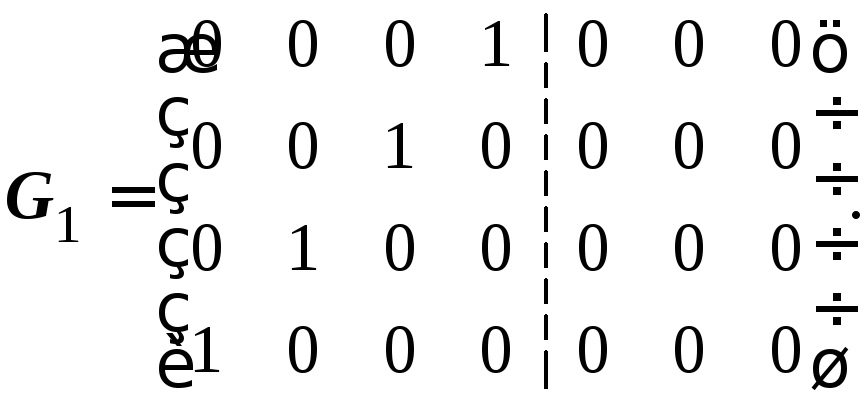 Выберем
образующий полином
Выберем
образующий полином
|
Таблица 5.6 |
| |||
|
Номер строки |
1 |
2 |
3 |
4 |
|
Код остатка |
011 |
110 |
111 |
101 |
 .
.
Полученная производящая матрица состоит
из четырёх строк (кодов). Все остальные
![]() =11
кодов, кроме кода 0000000, могут быть получены
линейной комбинацией строк производящей
матрицы
=11
кодов, кроме кода 0000000, могут быть получены
линейной комбинацией строк производящей
матрицы![]() .
.
