1. Теория информации

1.1 Теорема Котельникова

Согласно теореме Котельникова, если спектр сигнала ограничен полосой , то сигнал может быть восстановлен по своим отсчётам, разделёнными интервалом времени:

, (1.1)

где .

Предполагается , что число отсчетов бесконечно, (интервал наблюдения - бесконечен ).

Ввиду того, спектр сигнала ограничен полосой (вне этой полосы он равен нулю), спектральную функцию сигнала можно представить как периодическую функцию. При увеличении интервала дискретизациибольше, чем, спектральные функции сигнала на каждом периоде перекрываются, что приводит к искажению восстановленного сигнала. С уменьшением интервала дискретизациикачество восстановленного сигнала улучшается.

Если сигнал ограничен временем наблюдения , то можно осуществить периодическое продолжение его с периодом, равным. В этом случае производится дискретизация спектральной функции с интервалом, и производится восстановление спектральной функциипо его отсчётам в частотной области:

,

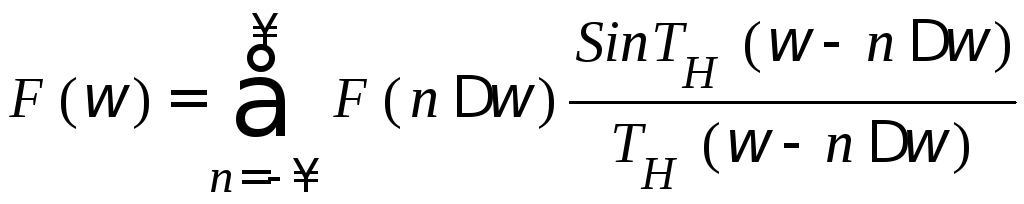где .

Восстановление спектральной функции будет улучшаться, если интервал дискретизации уменьшать по сравнению с.

Рассмотрим приложение теоремы Котельникова к случайным процессам. Трудность непосредственной записи формулы (1.1) в применении к случайным процессам связано с тем, что имеется множество реализаций, случайного процесса.

Поэтому применяется понятие сходимости в среднеквадратическом [*Левин кн 2 ]

Положим, - непрерывный в среднеквадратическом, стационарный, хотя бы в широком смысле, случайный процесс со спектральной плотностью мощности,.

Если существует предел

,

тогда случайный процесс определяется счётным множеством случайных величин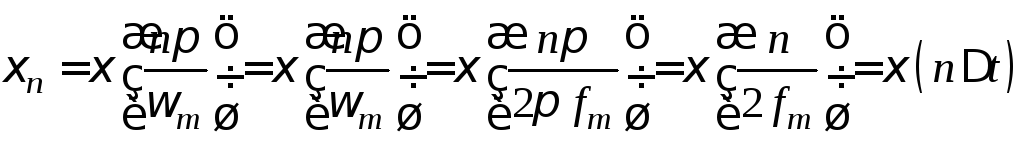и записывается как

. (1.2)

В качестве критерия возможности представления случайного процесса в виде разложения (1.1) выберем равенство корреляционных функций процессаправой части равенства (1.1). Положим,- корреляционная функция процесса.

Обозначим правую часть (1.1) через . Корреляционная функция процесса равна

=

. *

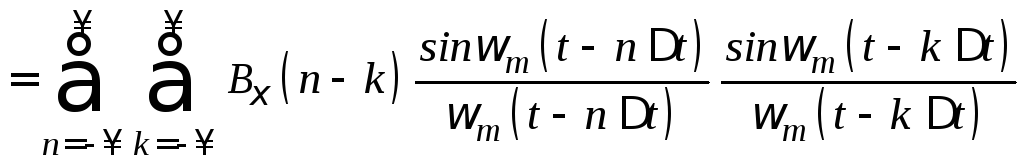Сделаем замену

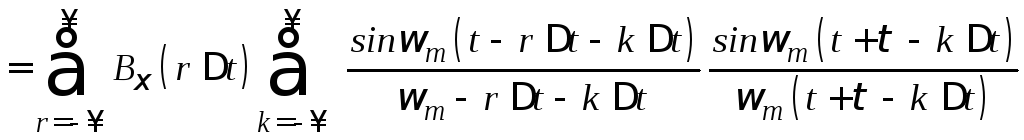
Для произвольной задержки справедливо разложение функциив ряд Котельникова и его представление в виде(Левин Б.Р. Статистические основы радиотехники, книга 2, стр.273 )

Применяя это соотношение к , получим

.

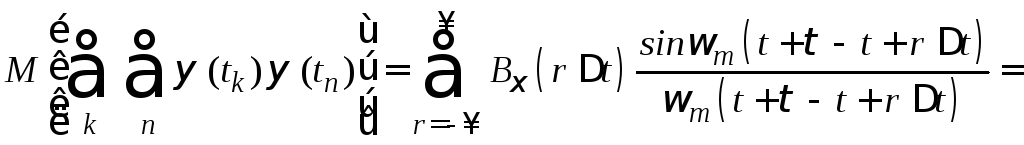
Но учитывая, что корреляционная функция – четная функция, имеем

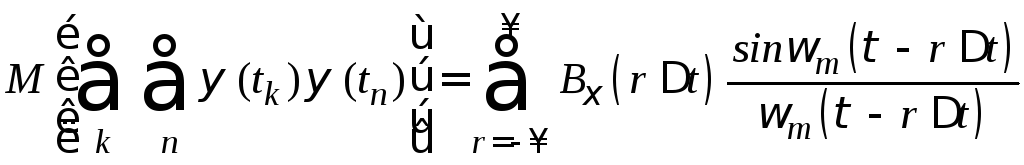. (1.3)

Но (1.6) - есть разложение корреляционной функции по ортогональным функциям видат.е.

=.

Исходя из принятого критерия, получим равенство (1.1)

1.2 Квантование сигнала по уровню

Положим, дискретизация сигналов по времени произведено, и необходимо передавать сигналы в дискретные моменты времени. Можно передавать сигналы, используя амплитудно-импульсную модуляцию (АИМ). Однако в настоящее время широко внедряются в практику кодово-импульсная модуляция (КИМ). Суть в следующем. Значения импульсов, полученных в результате дискретизации, переводятся в последовательность стандартных импульсов. Каждому значению параметра сигнала после дискретизации по времени соответствует определённый набор импульсов. Но при переходе от непрерывного представления параметра к дискретному возникает проблема, как выбирать порог дискретизации.

Для этого все возможные непрерывные значения параметра сигнала разбиваются на неперекрывающиеся интервалы квантования длиной , где - число интервалов квантования. Длины интервалов квантования могут быть неравными. Внутри каждого интервала квантования произвольно выбирается точка- уровень квантования. Если значение параметра сигнала попадает в-ый интервал, оно заменяется величиной. В результате имеется дискретный набор возможных значений параметра сигнала. Но в результате квантования возникает ошибка квантования, связанная с замещением истинного значения параметра его приближенным значением. Рассмотрим отдельно-ый интервал. Обозначим границы-ого интервала через,,, рисунок 11. Величина-ого интервала квантования будет равна

Ошибка квантования, истинное значениеи уровень квантованиясвязаны соотношением

. (1.4)

Как видно из (1.7) и рисунка 1.1 ошибка квантования на интервале квантования зависит от положения уровня квантования. Поэтому возникает вопрос, как расположить уровень квантования относительно границ,.

Положим, непрерывные значения сигнала распределены по неизвестному закону с плотностью распределения вероятности . Математическое ожидание ошибки квантования, с точки зрения теории измерений, определяет систематическую ошибку, а дисперсия ошибки квантования - динамическую ошибку, т.е. разброс случайных значений параметра сигнала около математического ожидания. Примем в качестве критерия выбора положения уровня квантованияравенство нулю систематической ошибки

. (1.5)

Ввиду того, что плотность распределения вероятности не известна и интервалы квантованиядостаточно малы, примем значения плотности распределения вероятностипостоянной в интервале, равной, где. В результате из (**.2) получим

. (1.6)

Решением этого приближенного равенства будет

. (1.7)

Из выражения (**.4) видно, что уровень квантования при сделанных допущениях должен находиться в середине интервала квантования.

Дисперсия ошибки квантования (динамическая ошибка) с учетом сделанных выше предположений равна

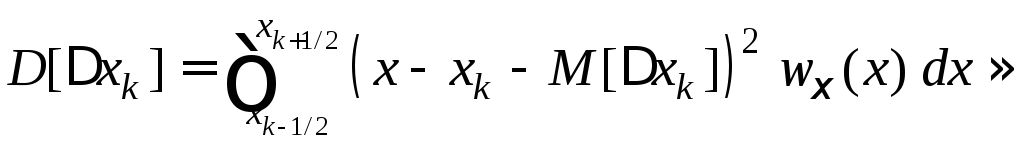
. (1.8)

Ввиду того, что интервалы квантования не перекрываются, ошибки квантования будут независимыми и общая дисперсия ошибки квантования равна сумме дисперсий ошибок квантования на каждом интервале, т.е.

. (1.9)

Выбор длин интервалов квантования зависит от априорных данных. Существуют различные методы выбора интервалов квантования. В самом простейшем случае интервалы квантования могут быть равны между собой, т.е.. Тогда выражение (**.6) будет иметь вид

. (1.10)

Произведение - приблизительно равно вероятности того, что измеряемая величина принадлежит интервалу. Погрешность аппроксимации зависит от величины интервала. По условию нормировки

. (1.11)

Используя (**.7) и (**.8) , получим

. (1.12)

Среднеквадратическая ошибка квантования равна

.