4.5 Теорема Шеннона о пропускной способности частотно ограниченного канала

Передача информации тесно связана с использованием физических сигналов. Свойства сигналов определяют канал связи. Известно, сигнал может быть представлен во времени и через спектральное разложение. Рассмотрим влияние ограничения на сигнал во временной и частотной областях и влиянии этих ограничений на пропускную способность канала связи.

1)Положим, сигналопределён в интервалеи задана полоса частот , занимаемая сигналом. Тогда, согласно теореме Котельникова, сигналможет быть разложен по функциям типасо значениями коэффициентов разложения, равными значениям сигнала в точках отсчета,

, (4.26)

где ,.

Ограничим время наблюдения интервалом (0, ). Тогда число отсчетов на интервале наблюдения равно

(4.27)

и в разложении сигнала число отсчётов ограничено:

. (4.28)

Если стоит вопрос о точном восстановлении сигнала по его отсчетам, то это невозможно, так как часть отсчётов будет утеряна.

Получили ряд (**.3), ограниченный по частоте и во времени

Мощность n-ой составляющей равна.

2)Положим задано время наблюдениясигнала. Из теории рядов Фурье известно, что можно построить периодическое продолжение функциис периодом. Разложим сигналв ряд Фурье

, (4.29)

где .

Коэффициенты разложения вычисляются по формуле

Чтобы ряд (**.4) сходился, необходимо выполнения условия - последовательность должна быть убывающей и.

Выберем достаточно большое число m, чтобы можно было пренебречь величиной. Тогда , или .

Разложение сигнала ограничено числом отсчетов

(4.30)

Получили ряд, ограниченный по частоте и по времени.

Мощность k-ой составляющей равна. Мощность сигнала равна мощности составляющих

3)Так как шум, присутствующий в канале, также ограничен по частоте и во времени определим числовые характеристики шума. Считается, что число отсчётов уже известно, т. е. определены и.

Примем , шум – «белый», т.е..

Разложение шума по гармоническим составляющим

, (4.31)

коэффициенты разложения равны

.

Согласно определению случайного процесса математическое ожидание и дисперсия коэффициентов разложения будут равны

,

. (4.31)

Мощность шума в канале связи равна

. (4.32)

4)Теорема Шеннона для частотно ограниченного канала.

Если мощность сигнала на входе канала не превосходит величины , то пропускная способность частотно ограниченного канала с аддитивным белым гауссовым шумом удовлетворяет неравенству

. (4.33)

Знак равенства будет в том случае, когда значения сигнала распределены по нормальному закону.

Согласно определению пропускной способности

(4.34)

Энтропия - это энтропия множества отсчетов в моменты временис интерваломиз ансамблядля всех моментов времени. Ввиду того, что неизвестны вероятностные характеристик процесса, справедливы выражения

. (4.35)

. (4.36)

.

Используем свойство: среднегеометрическое не превышает среднеарифметическое. Тогда

(4.37)

При вычислении условной энтропии используется независимость символов попарно на входе и выходе канала связи.

=(4.38)

Условная энтропия зависит от шума и распределена по нормальному закону (ссылка на канал связи ****) согласно условиям теоремы. Энтропия случайной величины, распределённой по нормальному закону, равна

. (4.39)

После подстановки (**.5) в (**.14) получим

(4.40)

Подставим выражения (**.13) и (**.16) в (**.10):

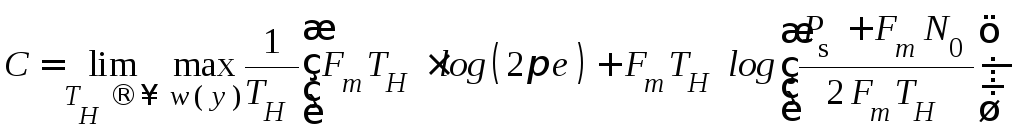
В результате получим

(4.41)

Если сигнал на входе канала связи распределён по нормальному закону, пропускная способность канала равна

(4.42)

Как видно из формулы, пропускная способность канала зависит от полосы частот, занимаемой сигналом, мощности сигнала и спектральной плотности мощности «белого» шума.