4.1 Скорость передачи информации и пропускная способность канала связи

Ввиду того, что канал связи считается стационарным, на вход канала поступает последовательность символов , где каждый символ, образуетn-разрядный код. Количество комбинаций, которое можно образовать с использованием кода с основаниемD, равно. Множество этих комбинаций образует пространство значений кодовых комбинаций. Символы при ансамблеYобозначают моменты времени реализации величины. Например, для двумерного ансамбляcоснованием кода, равнымD=3, имеем

.

На выходе канала имеем последовательность символов , где каждый символ. Точно так же можно образовать множество кодовых комбинаций, составляющих пространство.

Последовательность символов поступает в канал в течение.

Количество информации, которое передается по каналу связи, за время наблюдения согласно (1.18) равно

. (4.2)

Скоростью передачи информации по каналу связи называется величина

. (4.3)

Скорость передачи информации Rотражает среднюю скорость передачи информации в единицу времени.

Максимальная скорость передачи информацииназывается пропускной способностью канала связи

. (4.4)

Рассмотрим в выражении (1.18) разность . Чем больше энтропия, тем больше пропускная способность канала связи. Величина определяет среднюю неопределённость, содержащуюся в ансамблеY, которая зависит от распределения вероятности элементов ансамбляY. Поэтому максимизация скорости передачи информации происходит по распределению вероятности элементов ансамбляY.

Упростим выражение (4.2).

. В силу того, что канал - стационарный и реализации элементов ансамблейив моменты времениинезависимы. Тогда

.

Но ансамбли за время передачи информации неизменны, т.е.. Тогда имеем

(4.5)

Условная энтропия в (4.2) представляется как

==

=.

Воспользуемся условием независимости символов попарно на входе и выходе канала связи, а также стационарностью канала. Тогда соответствующие вероятности и условная энтропия будут равны

=,

=,

==

==. (4.6)

Если отсчёты во времени эквидистантны, то , где- интервал дискретизации по времени. Подставив (4.5), (4.6) ив (4.4), получим

. (4.7)

Введём скорость передачи символов

.

Тогда пропускную способность можно записать как

(4.8)

В таблице 4.1 представлены характеристики источника сообщений, кодера источника и канала связи.

Таблица 4.1

4.2 Канал без шумов

Шум в канале связи искажает физические параметры сигнала, что в свою очередь приводит к искажению символов. Вероятностная характеристика искажений – это условная вероятность . Будем считать, сигнал в канале не искажается, если. Тогда для канала без шумов справедливо выражение

(4.9)

Из выражения (**.9) следует, , т.е. пропускная способность канала связи равна

=(4.10)

Если используется код с основанием D,то энтропия ансамблядостигает наибольшего значения при. Тогда пропускная способность канала равна

. (4.11)

Теорема Шеннона о кодирование источника независимых сообщений для канала без шумов. (Шеннон, стр. 270)

Пусть источник имеет энтропию , а канал имеет пропускную способность. Тогда можно закодировать сообщения таким образом, что можно передавать их со средней скоростью

, где .

Передавать сообщения со скоростью большей, чем , невозможно.

Доказательство. Будем считать источник сообщений согласованным с каналом по скорости передачи информации, если . Тогда

. (4.12)

Энтропия не превышает. Запишем

=,. (4.13)

где .

Подстановка (4.13) в (4.12) позволяет получить

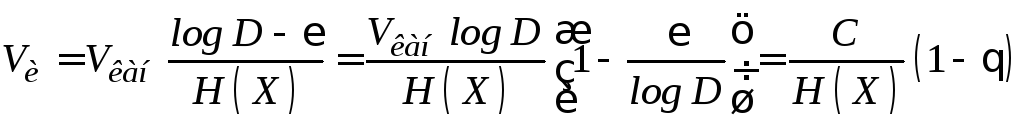, (4.14)

где .

Если принять , то, т.е. не имеет смысла передавать сообщения.