Билет №1. Абстрактный автомат. Формы представления и моделирование автомата.

//Ильяс

Мат. моделью дискретного управляющего устройства явл. абстрактный автомат, кот. задается множеством из элементов: S = {A, Z, W, , , а1}, где А = {а₁ ,..., а_m ,..., а_M} – мн-во состояний; Z = {z₁ ,..., z_f ,..., z_F} – мн-во входных сигналов; W = {w₁ ,..., w_g ,..., w_G} – мн-во выходных сигналов;  - ф-ия переходов, реализующая отображение множества D   А x Z в А (а_s =  (а_m , z_f), а_s  А); ( - ф-ия выходов, реализующая отображение множества D   А x Z на W (w_g = (а_m , z_f )); - это не всегда) а₁  А - начальное состояние автомата. Автомат называется конечным, если конечны множества А, Z, W . Автомат назыв. полностью определенным, если области определения функции  и  совпадают со множеством А x Z - множеством всевозможных: пар вида (a_m, z_f ) . У частичного автомата ф-ии  или  определены не для всех пар (а_m , z_f )  А x Z. Абстрактный автомат имеет один входной и один выходной канал. В каждый момент t = 0, 1, . . . времени автомат находится в определенном сост. a(t) из мн-ва А, причем в нач. момент t= 0 он всегда находится в нач. сост. а(0) = а1 . Абстрактн. автомат реализует некоторое отображение мн-ва слов входного алфавита Z во множество слов выходного алфавита W.

Чтобы задать конечный автоматS, необходимо описать все элементы множества S = {A, Z, W, , , а1}. Наиболее часто используются табличный, графический и матричный способы задания автомата. 

Табличный: строки этих таблиц соответствуют входным сигналам, а столбцы - состояниям, причем крайний левый столбец состояний обозначен начальным состоянием а1.

вид таблицы переходов автомата Мили	вид таблицы выходов автомата Мили

Графический: граф автомата - ориентированный связный граф, вершины которого соответствуют состояниям, а дуги - переходам между ними.

Граф автомата Мили	Граф автомата Мили

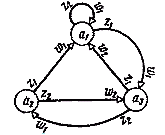
Две вершины графа автомата а_m и а_s (исходное состояние и состояние перехода) соединяются дугой, направленной от а_m к а_s, если в автомате имеется переход из а_m в а_s. Если переход автомата из сост. а_m в сост. а _s происходит под действием. нескольких входных сигналов, то дуге (а_m а_s ) приписываются все эти входные и соответствующие выходные сигналы. При описании автомата Мура в виде графа выходной сигнал w_g = (а_m) записывается внутри вершины или рядом с ней.

Матричный: матрица соединений автомата это квадратная матрица, строки кот. соответствуют исходным состояниям, а столбцы - состояниям перехода. Элемент с_ms= z_f / w_g, стоящий на пересечении m-ой строки и s-го, в случае автомата Мили соответствует входному сигналу z_f, вызывающему переход из состояния а_m в состояние а_m, и выходному сигналу w_g, выдаваемому на этом переходе.

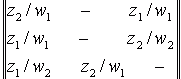
//Альбина

Абстрактный автомат. Формы представления и моделирование автомата.

состояние автомата.

Модель Мили. Законы функционирования автомата Мили представлены следующим образом: q(t+1) = δ(q(t), x(t)) y(t) = λ(q(t), x(t)) t – текущий момент времени; t+1 – следующий момент времени; q(t+1) – состояние автомата в следующий момент времени; q(t), x(t), y(t) – элементы описания автомата в текущий момент времени.

Модель Мура. Законы функционирования автомата Мура представлены следующим образом: q(t Абстрактный автомат (АА) – дискретный преобразователь информации; представляет собой множество, состоящее из шести элементов: Для задания конечного автомата всеэлементы множества должны быть заданы явно. Так дляавтомата Мили: - алфавит состояний; - выходной алфавит; - входной алфавит; - функция переходов автомата из одного состояния в другое -функция выходов - начальное +1) = δ(q(t), x(t)) y(t) = λ(q(t)) В модели Мура выходной сигнал явно зависит только от состояния, а косвенно –  и от входного сигнала.

Например, автомат Мили , представленный втабл.1.3 в явной форме описывается так:

Автомат Мура , представленный втабл.1.8 в явной форме описывается так:

Табличная форма.

Автомат Мили задается таблицей переходов (табл.6.1) и таблицей выходов (табл.6.2)

Таблица 6.1

ТП	а0			а1	а2
х0	а0			а1	а2
х1	а1			а2	а0
х2	а2			а0	а0
х3	а0			а0	а0

ТВ	а0	а1	а2
х0	у0	у0	у0
х1	у0	у0	у1
х2	у0	у1	у1
х3	у1	у1	у1

Таблица 6.2

На пересечении столбца и строкв таблице переходов записывается состояние переходаa_s(t+1)=[am(t), x_f(t)], в которое автомат переходит из состояния a_m под действием сигнала x_f, а в столбце выходов – соответствующий этому переходу выходной сигнал y(t)=[a_m(t), x_f(t)]

Таблицы 6.1 и 6.2 определяют функционирование простого автомата для продажи газет стоимостью 30 центов. Когда сумма монет, опущенных в автомат (различаются монеты стоимость 10, 20, и 30 центов) равна или больше 30 центов, автомат генерирует выходной сигнал y₁ и выдает газету. В остальных случаях генерируется сигнал y₀.

Когда на входе присутствует сигнал x₀ (отсутствие монеты), генерируется выходной сигнал y₀ (отсутствие газеты).

Как нам известно, выходной сигнал автомата Мура зависит только от внутреннего состояния. Поэтому автомат Мура может быть задан одной отмеченной таблицей переходов (табл.6.3).

Таблица 6.3

	ОТП					u1				u1			u3		u2			u3
						a1				a2			a3		a4			a5
	x1					a2				a5			a3		a3			a3
	x2					a4				a2			a2		a1			a1

ТП	u1	u1	u3	u3	u2	u2
	a1	a2	a3	a4	a5	a6
х1	a6	a6	a4	a3	a4	a1
х2	a4	a3	a5	a5	a5	a2

С-автомат задается двумя таблицами (отмеченной таблицей переходов и таблицей выходов или наоборот таблицей переходов и отмеченной таблицей выходов(табл..6.4 и табл..6.5))

Таблица 6.4

Таблица 6.5

ТВ	a1	a2	a3	a4	a5	a6
x1	y1	y1	y2	y1	y2	y2
x2	y2	y1	y1	y2	y1	y1

Графовая форма задания абстрактных автоматов

В данном случае автомат представляетсяграфом, в котором:

множество изображеновершинами графа;

функция заданадугами графа, причем две вершины графа и, соединяются дугой, если в автомате существует переход изв;

множество изображено меткамидуг: ставится надуге из вершины в вершину, если в автомате существует переход извпод действием входного сигнала;

функция задана меткамидуг или вершин: для автомата Мили дуга из вершины в вершинупомечается выходным сигналом, если в автомате существует переход изви при этом вырабатывается выходной сигнал; а дляавтомата Мура выходным сигналом помечается вершина, определяющая.

На табл.1.8 приведены примеры описания автомата Мили и автомата Мура:

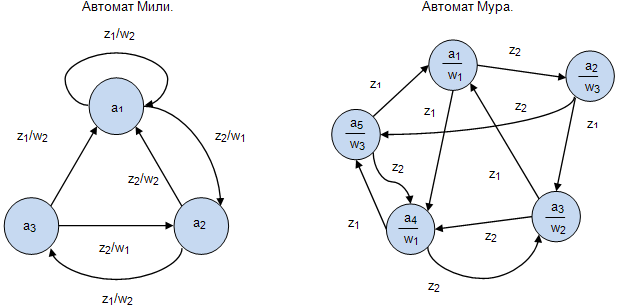
Рис. 1.8.

Матричная форма

Для автомата Мили матричная форма состоит из матрицы размерностью , где каждый элементматрицы стоящий напересечении -ой строки и-го столбца соответствует входному сигналу, вызывающему переход из состоянияв состояниес выработкой выходного сигнала. Пример матричного описанияавтомата Мили показан ниже.

Для автомата Мура матричная форма состоит из матрицы размерностью , где каждый элементматрицы , стоящий напересечении -ой строки и-го столбца, соответствует входному сигналу, вызывающему переход из состоянияв состояниеТак как выходной сигнал. вавтомате Мура зависит только от состояния, следовательно, выходные сигналы могут быть представлены матрицей-столбцом.

Билет №2. Абстрактный автомат. Автоматы Мура, Миля.

Определение. Абстрактным конечным автоматом называется шестерка объектов

A={S, s₀, X, Y, φ,ψ},

где S – конечное непустое множество состояний;

s₀€S – начальное состояние;

X – конечное непустое множество входных сигналов;

Y – множество выходных сигналов;

φ : SˣX →S– функция переходов;

ψ : SˣX →S – функция выходов.

По способу формирования функций выходов среди синхронных автоматов выделяют автоматы Мили и автоматы Мура

// (первый источник)

В автомате Мили функция выходов ψ определяет значение выходного символа по классической схеме абстрактного автомата. Она является двухаргументной и символ y (t) в выходном канале обнаруживается только при наличии символа во входном канале x (t). Функции перехода и выхода для автомата Мили можно записать в виде

s(t+h) φ(s(t),x(t));

y(t+h) ψ(s(t),x(t)), где h – длительность такта.

Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура. В автоматах этого типа функция выходов определяет значение выходного символа только по одному аргументу – состоянию автомата. При этом символ y (t) в выходном канале существует все время, пока автомат находится в состоянии s (t ). Для автомата Мура функции перехода и выхода можно записать как

s(t+h) φ(s(t),x(t));

y(t+h) ψ(s(t)).

Считается, что реализация автоматов Мили, как правило, более проста, но в них возникают проблемы с синхронностью формирования выходных сигналов. Между моделями Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой или обратно.

//(второй источник)

Автомат Мура (абстрактный автомат второго рода) в теории вычислений — конечный автомат, выходное значение сигнала в котором зависит лишь от текущего состояния данного автомата, и, не зависит напрямую, в, отличие от автомата Мили, от входных значений.

Формальное определение:

Автомат Мура может быть определен как кортеж из 6 элементов, включающий:

- множество внутренних состояний S (внутренний алфавит);

- начальное состояние S0;

- множество входных сигналов X (входной алфавит);

- множество выходных сигналов Y (выходной алфавит);

- функция переходов Φ(z, x).

- Для любого автомата Мура существует эквивалентный ему автомат Мили и наоборот. Любой автомат Мура путем добавления ряда внутренних состояний может быть преобразован в автомат Мили.

Способы задания:

- Диаграмма — изображённый на плоскости ориентированный граф, вершины которого взаимно однозначно соответствуют состояниям автомата, а дуги — входным символам.

- Таблица переходов-выходов, в ячейках которой для каждой пары значений аргументов х(t), s(t) проставляются будущие внутренние состояния s(t+1). Значения выходных сигналов y(t) представляются в отдельном столбце.

Таблица переходов

	Y1	Y2	Y3	Y1	Y2	Y2	Y3
	a1	a2	a3	a4	a5	a6	a7
1	a5	a4	a5	a3	a4	a2	a5
2	a7	a1	a4	a2	a1	a3	a4

Автомат Мили (англ. Mealy machine) — конечный автомат, выходная последовательность которого (в отличие от автомата Мура) зависит от состояния автомата и входных сигналов. Это означает, что в графе состояний каждому ребру соответствует некоторое значение (выходной символ). В вершины графа автомата Мили записываются выходящие сигналы, а дугам графа приписывают условие перехода из одного состояния в другое, а также входящие сигналы.

Автомат Мили можно описать пятеркой (Q,X,Y,f,g), где Q - множество состояний автомата, X - множество входных символов, Y - множество выходных символов, q=f(Q,X) - функция состояний, y=g(Q,X) - функция выходных символов.

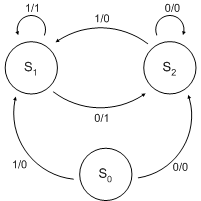Кодировка автомата Мили:

Вершина (операторная или логическая), стоящая после вершины "Начало", а также вход вершины "Конец" помечается символом S1, вершины, стоящие после операторных помечаются символом Sn (n=2,3..).

Матрица функций переходов

Q / X	C1	C2	C3
q1	q1 / S	q2 / U1	q3 / U2
q2	q1 / D1	q2 / S	q3 / U1
q3	q1 / D2	q2 / D1	q3 / S

Билет №3.Абстрактный автомат. Переводы автомата Мура в автомат Миля и обратно.

1.3.4. Переход от а Мура к а Мили

Задан автомат

S_A={A_A, Z_A, W_A, _A, _A, a_1A} ,

где

A_A = {а₁ , :, а_m , : , a_M},

Z_A= {z₁ , :, z_f , :, z_F},

W_A = {w₁ , :, w_g , : , w_G} ;

_A - реализует отображение A_A х Z _A в A_A, _A - отображение A _A на W_A, а a_1A = a₁ - начальное состояние.

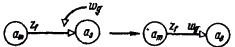Рис. 1-6. Граф автомата Мура S₅ Рис. 1-7. Иллюстрация перехода от модели Мура к модели Мили

Построим автомат Мили

S_B={A_B, Z_B, W_B, _B , _B, a_1B},

у которого

A_B = A_A = {а₁ , :, а_m , : , a_M},

Z_B= Z_A = {z₁ , :, z_f , :, z_F},

W_B = W_A = {w₁ , :, w_g , : , w_G};

_B = _A, a_1B = a _1A = a₁

Функцию выходов Мили _B определим следующим образом. Если в автомате Мура _A(a_m,z_f)=a_s и _A(a_s)=w_g, то в автомате Мили _B(a_m,z_f)=w_g.

Переход от автомата Мура к автомату Мили при графическом способе задания иллюстрируется рис.1-7: выходной сигнал (w_g), записанный рядом с вершиной (а_s), переносится на все дуги, входящие в эту вершину. На рис. 1-8 приведен граф автомата Мили S₆, эквивалентного автомату Мура S₃ (рис. 1-4).

При табличном способе задания автомата S_A таблица переходов автомата S_B совпадает с таблицей переходов S_A, а таблица выходов S_B получается из таблицы переходов заменой символа a_s, стоящего на пересечении строки z_f и столбца a_m, символом выходного сигнала w_g, отмечающего столбец a_s , в таблице переходов автомата S_A.

Из самого способа построения автомата Мили S_B очевидно, что он эквивалентен автомату Мура S_A. Действительно, если некоторый водной сигнал z_f Z поступает на вход автомата S_A, находящегося в состоянии а_m, то он перейдет в состояние а_s= _A(а_m,z_f) и выдаст входной сигнал w_g= _A(а_s). Но соответствующий автомат Мили S_B из состояния a_m, также перейдет в состояние a_s, поскольку _B(а_m,z_f) = _A(а_m,z_f) = а_s- и выдаст тот же выходной сигнал w_g согласно способу построения функции _В. Таким образом, для входной последовательности длины один поведение автоматов S_A и S_Bполностью совпадает. По индукции нетрудно показать, что любое входное слово конечной длины, поданное на входы автоматов S_A и S_B , установленных в состояния a_m, вызовет появление одинаковых выходных слов и, следовательно, автоматы S_A и S_A а_m эквивалентны.

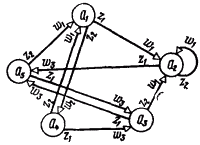
Рис. 1-8. Автомат Мили S₆эквивалентный автомату Мура S₅

Рис. 1-9. Построение множества A_s

1.3.5. Переход от а Мили к а Мура

Прежде чем рассмотреть трансформацию автомата-Мили в автомат Мура, наложим на автомат Мили следующее ограничение: у автомата не должно быть преходящих состояний. Под преходящим будем понимать состояние, в которое при представлении автомата в виде графа не входит ни одна дуга, но которое имеет по крайней мере одну выходящую дугу (пример - состояние a₁ на рис. 1-3). Итак, пусть задан автомат Мили

S_A={A_A, Z_A, W_A, _A, _A, a_1A} ,

где

A_A = {а₁ , :, а_m , : , a_M},

Z_A= {z₁ , :, z_f , :, z_F},

W_A = {w₁ , :, w_g , : , w_G};

_A - реализует отображение A_A х Z_A в A_A, _A - отображение A_A на W_A , а a_1A = a₁ - начальное состояние.

Построим автомат Мура

S_B={A_B, Z_B, W_B, _B, _B, a_1B},

у которого

Z_B= Z_A = {z₁ , :, z_f , :, z_F},

W_B = W_A = {w₁ , :, w_g , : , w_G};

Для определения А_B каждому состоянию a_sA_A поставим в соответствие множество A_s всевозможных пар вида (а_s,w _g), где w_g - выходной сигнал, приписанный входящей в а_s дуге (рис. 1-9): А_s={(a_s, w_g) | (a_m, z_f) = a_s и (a_m, z_f) = w_g}

Число элементов в множестве А_s равно числу различных выходных сигналов на дугах автомата S _A, входящих в состояние a_s. Множество остояний автомата S_B получим как обединение множеств A_S (s=1,:,M):

Рис. 1-10. Иллюстрация перехода от модели Мили к модели Мура

Функции выходов _B и переходов _B определим слудиющим образом. Каждому состоянию автомата Мура S_B , представляющему собой пару вида (a_s, W_g), поставим в соответствие выходной сигнал W_g. Если в автомате Мили S_A был переход а1_B (а_m, z_f) = W_k , то в S_B (рис. 1-10) будет переход из множества состояний A_m , порождаемых a_m , в состояние (a_s, W_k) под действием входного сигнала z_f.

В качестве начального состояния а1_B можно взять любое из состояний множества А1, которое порождается начальным состоянием а1 автомата S_A. Напомним, что при сравнении реакции автоматовS_A и S_B на всевозможные входные слова не должен учитываться выходной сигнал в момент времениt=0, связанный с состоянием а1_B автомата S_B .

Билет №4.Абстрактный автомат. Автоматы без выхода. Распознающие автоматы.

Результат работы автомата без выхода определяется по его конечному состоянию. Конечный автомат относится к такому. Конечный автомат может быть задан в виде упорядоченной пятерки: M = {V, Q, q₀, F, d}, где

V — входной алфавит (конечное множество входных символов), из которого формируются входные цепочки, допускаемые конечным автоматом;

Q — множество состояний;

q₀ — начальное состояние (q₀ принадл. Q);

F — множество заключительных состояний (F включено в Q);

d — функция переходов, значение функции переходов на упорядоченной паре (состояние, входной символ или пустая цепочка) есть множество всех состояний, в которые из данного состояния возможен переход по данному входному символу или пустой цепочке (λ).

Конечн/ автомат начинает работу в сост. q₀, считывая по одному символу входной цепочки. Считанный символ переводит автомат в новое сост. в соотв. с ф-ией переходов. Читая входную цепочку x и делая один такт за другим, автомат, после того как он прочитает последнюю букву цепочки, окажется в каком-то состоянии q'. Если это состояние является заключительным, то говорят, что автомат допустил цепочку x.

Распознающим называется автомат Мура с множеством выделенных состояний, называемых конечными. Говорят, что автомат распознает входное слово, если, начав свою работу в одном из начальных состояний, он заканчивает ее в одном из конечных.

Распознающий автомат – это, как правило, недетерминированный частичный автомат. То есть по одному и тому же сигналу можно перейти в различные состояния, а в некоторых состояниях нет перехода для ряда входных сигналов.

Билет №5. Абстрактный автомат. Минимизация автоматов.

//Лекции

Теперь перейдём к описанию процесса минимизации конечного автомата.

1. Мы начнём с поиска и удаления всех недостижимых состояний.

2. Затем мы должны найти такое разбиение множества состояний автомата, чтобы каждое подмножество содержало неразличимые состояния, т.е. если s и t принадлежат некоторому подмножеству, то для всех a из  (s,a) и (t,a) также принадлежат этому подмножеству. Для этого мы разобьём множество состояний на два подмножества: F и S-F.

3. В дальнейшем, мы попытаемся разбить каждое из подмножеств, соблюдая указанное выше условие. Если возникает ситуация, при которой мы не можем разбить никакое множество состояний, то мы заканчиваем процесс разбиения.

4. В результате мы получим некоторый набор множеств состояний S₁…S_k. Каждое из S_i содержит только неразличимые состояния.

5. Наконец, внесём в множество состояний минимизированного автомата по одному представителю каждого из множеств S_i. На этом процесс завершается.