
- •Комбинаторика. Основные понятия.
- •Основные теоремы теории вероятностей. Свойства операций над событиями
- •Дискретные случайные величины. Закон распределения, математическое ожидание, дисперсия. Свойства математического ожидания, дисперсии.
- •Дискретные случайные величины.
- •Математическое ожидание m(X).
- •Точечные оценки. Выборочное среднее, генеральная средняя, выборочная дисперсия, генеральная дисперсия, исправленная дисперсия.
Комбинаторика. Основные понятия.
Комбинаторика – раздел математики, в котором рассматриваются различные комбинации элементов множества (или множеств), а так же способы подсчета их числа.
-
Правило суммы для выбора 2-х объектов. Если объект А можно выбрать n способами, а объект В - другими m способами, то выбор “или A, или B” можно осуществить n+m способами.
Замечание. Множество способов выбора объекта А и множество способов выбора объект B не должно иметь общей части.
-
Правило суммы для выбора m объектов. Если объект А1 можно выбрать n1 способами, объект А2 - другими n2 способами,…, объект Аm - nm способами, отличных от всех предыдущих, то выбор “или A1, или A2 , … или Am ” можно осуществить n1+n2+…+nm способами.
-
Правило произведения для выбора 2-х объектов. Если объект А можно выбрать n способами после этого при любом выборе объекта А объект В можно выбрать другими m способами, то выбор пары“ A и B” можно осуществить n
 m
способами.
m
способами. -
Правило произведения для выбора m объектов. Если объект А1 можно выбрать n1 способами, объект А2 - другими n2 способами,…, объект Аm - nm способами, отличных от всех предыдущих, то выбор всех элементов “ A1 , и A2 , и Am ” можно осуществить n1
 n2
n2 …
… nm
способами.
nm
способами. -
Перестановка. Перестановкой из n элементов называется некоторое расположение этих n элементов на n местах.
-
Размещение. Размещениями называются комбинации, составленные из n различных элементов, взятых по m, отличающиеся порядком и составом.
![]()
-
Сочетания. Сочетаниями называются комбинации, составленные из n различных элементов, взятых по m, отличающиеся только составом, а порядок не важен.
 .
.
Случайные события.
Вероятность – классическое определение.
Относительная частота.Случайные
события
–
это события, исход которых заранее
предсказать нельзя (например, попадание
в цель при выстреле).Существует три
способа определения вероятности:
аксиоматический, статический, классический.
Сейчас поговорим о
классическом определении.Определение:
Вероятность события A
– это![]() где
m
– число
элементарных событий благоприятствующих
А,
где
m
– число
элементарных событий благоприятствующих
А,
n
–
общее число равновозможных
событий.Относительной
частотой
события А
называется
отношение числа опытов, в которых
появилось событие А,
к общему числу опытов:![]() где
где
![]() - число появлений события А
n
– общее число
опытов.
- число появлений события А
n
– общее число
опытов.
Основные теоремы теории вероятностей. Свойства операций над событиями
Определение: Суммой двух событий A+B называется событие, состоящее в появлении хотя бы одного из них.Например: Если событие А – попадание в цель при первом выстреле, событие B – попадание в цель при втором выстреле, то C=A+B – попадание в цель вообще, безразлично при каком выстреле : при первом или при втором или при обоих вместе.
Определение: Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из них.
Определение:
Произведением
двух событий A![]() B
двух событий называется событие,
состоящее в совместном появлении события
А и
события B.Например:
Если событие
А –
появление дамы при вынимании карты из
колоды, событие B
– появление
карты пиковой масти, то C=A
B
двух событий называется событие,
состоящее в совместном появлении события
А и
события B.Например:
Если событие
А –
появление дамы при вынимании карты из
колоды, событие B
– появление
карты пиковой масти, то C=A![]() B
– появление пиковой дамы.
B
– появление пиковой дамы.
Определение:
Событие
![]() называется противоположным
для А,
если оно выполняется тогда и только
тогда, когда не выполняется событие А.
называется противоположным
для А,
если оно выполняется тогда и только
тогда, когда не выполняется событие А.
При вычислении вероятностей удобно бывает представить сложные события в виде комбинации более простых событий, применяя операции сложения, умножения, а так же противоположные событие.
Пример:
![]() - попадание при первом выстреле,
- попадание при первом выстреле,![]() - попадание при втором выстреле,
- попадание при втором выстреле,![]() - попадание при третьем выстреле..Пусть
событие В -
в результате трех выстрелов будет только
одно попадание:
- попадание при третьем выстреле..Пусть
событие В -
в результате трех выстрелов будет только
одно попадание:![]()
Свойства операций над событиями
-
 ,
, -
 - коммутативность,
- коммутативность, -
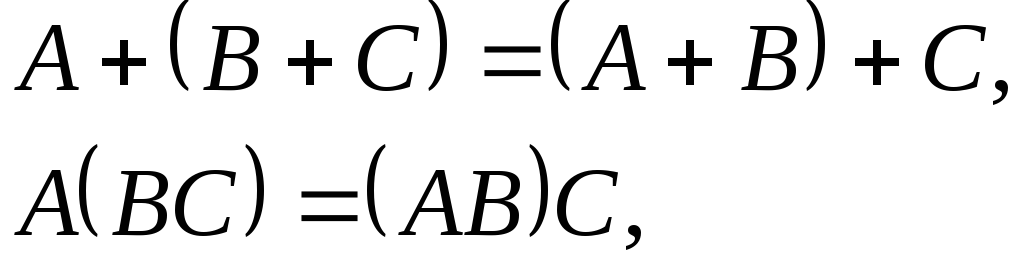 - ассоциативность
- ассоциативность -
 - дистрибутивность
- дистрибутивность -
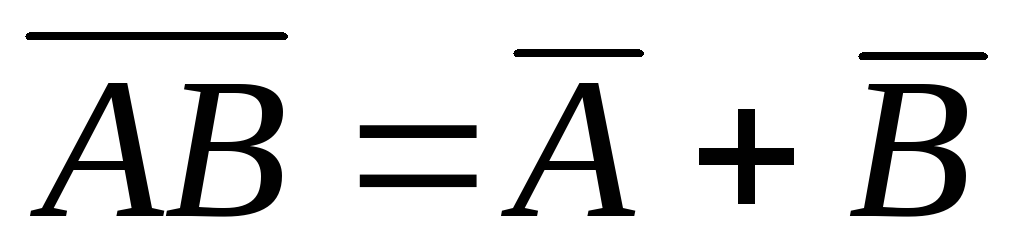 и
и
 ,
, -
 ,
, -

-
 где
где
 - достоверное событие,
- достоверное событие,
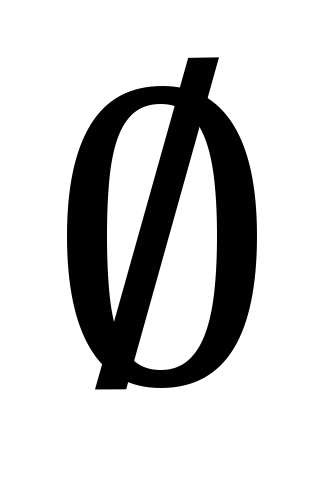 - невозможное событие.
- невозможное событие.
Теорема 1: Если события А и В несовместны, то вероятность их суммы равна сумме их вероятностей
Следствие:
Вероятность
появления одного из нескольких попарно
несовместных событий, безразлично
какого, равна сумме вероятностей этих
событий:![]() .
.
Полная группа событий. Условная вероятность.
Полная группа событий
Полной группой называется совокупность единственно возможных событий испытания.
Теорема 2:
Сумма вероятностей
![]() ,
образующих полную группу, равна единице:
,
образующих полную группу, равна единице:
![]() .
.
Теорема 3:
![]()
Теорема 4:
Вероятность
совместного появления двух независимых
событий равна произведению вероятностей
этих событий:
![]() .
(без доказательства).
.
(без доказательства).
Определение: Событие A называется зависимым от события B, если вероятность события A меняется в зависимости от того, произошло событие B или нет.
Определение:
Условной
вероятностью
![]() называется вероятность события A
, вычисленную
при условии, что событие B
произошло.
называется вероятность события A
, вычисленную
при условии, что событие B
произошло.
Теорема 5:
![]() .
.
Следствие:
![]() ,
,
![]() .
.
Эти формулы можно распространить на любое число событий:
![]()
Определение: События A и B называются независимыми, если вероятность каждого из них не зависит от того, произошло другое событие или нет, т.е.
![]() ,
т.е.
,
т.е.
![]() (теорема
4).
(теорема
4).
Теорема 6: Вероятность двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
![]() .
.
Формула полной вероятности. Формулы Бейеса.
Формула полной вероятности.
Теорема: Пусть
событие A
может наступить при условии появления
одного из несовместных событий
![]() ,
которые образуют полную группу.
,
которые образуют полную группу.
Пусть известны
вероятности
![]() ,
тогда
,
тогда![]() -
-
формула полной вероятности.
Доказательство:
Т.к. по условию
событие A
может наступить, если наступит одно из
несовместных событий
![]() ,
то появление события A
означает осуществление одного, безразлично
какого из несовместных событий
,
то появление события A
означает осуществление одного, безразлично
какого из несовместных событий
![]() ,
т.е.
,
т.е.
![]()
Формулы Бейеса
Пусть событие A
может наступить при условии появления
одного из несовместных событий
![]() ,
которые образуют полную группу. Так
как неизвестно, какое из этих событий
произойдет, их называют гипотезами.
,
которые образуют полную группу. Так
как неизвестно, какое из этих событий
произойдет, их называют гипотезами.
Допустим, что произошло испытание, в результате которого появилось событие A. Поставим своей задачей определить как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез, т.е. будем искать
![]()
Ясно, что
![]() .
Значит,
.
Значит,![]() ,
но
,
но![]() ,
т.е.
,
т.е. .
.
Аналогично, для
![]() Или
в общем виде можно записать
Или
в общем виде можно записать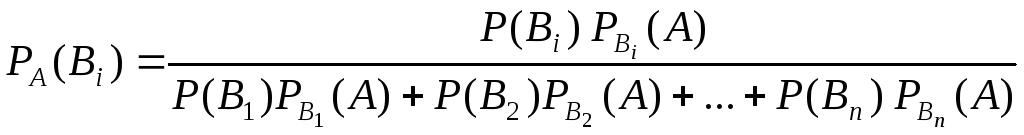 -формулы Бейеса.
-формулы Бейеса.
Повторение испытаний. Формула Бернулли.
Пусть проводится
n
независимых испытаний, в каждом из
которых с одной и той же вероятностью
p
может произойти событие А
или произойти событие
![]() с вероятностью
с вероятностью
![]() .
Такого рода схема называется схемой
Бернулли.
.
Такого рода схема называется схемой
Бернулли.
Тогда вероятность
того, что событие A
наступит ровно k
– раз вычисляется по формуле Бернулли:![]() .
.
Доказательство:
Заметим, что не
требуется, чтобы событие A
повторялось ровно k
раз в определенной последовательности.
Например, если мы хотим, чтобы событие
A
появилось 3 раза в четырех испытаниях,
то это может быть![]() .
.
По аналогии, если
в одном испытании событие A
появилось k
раз, то вероятность:
![]() .Таких
событий может быть:
.Таких
событий может быть:
![]() .
.
