Казанский государственный университет

Факультет вычислительной математики и кибернетики

Кафедра теоретической кибернетики

В.С. Кугураков, Р.К. Самитов, Р.Б. Ахтямов, В.Р. Байрашева

Практикум работы на ЭВМ.

Задание 2. Процедуры и функции.

Казань 2007.

УДК (075.8) 004.3

Кугураков Владимир Сергеевич

Самитов Ринат Касимович

Ахтямов Рауф Баграмович

Байрашева Венера Рустамовна

Практикум работы на ЭВМ. Задание 2. Процедуры и функции. Казань: КГУ. 2007 - с.

Пособие предназначено для студентов, обучающихся по специальности «Прикладная математика и информатика» и направлению «Информационные технологии», а также для преподавателей, ведущих практические занятия по информатике, алгоритмическим языкам и программированию.

Компьютерная верстка и дизайн обложки: Ахтямова Светлана Станиславовна.

1 Т и п о в ы е з а д а ч и

1.1 Табулирование интегральной функции.

Вычислить значение функции

в заданных точках t₁, …, t_m с точностью . Входными данными программы являются числа m, a, b,  и массив t[1: m]. Выходные данные – массив y[1: m], где . В программе предусмотреть:

- процедуру-функцию, вычисляющую значение F(x, t), с формальными параметрами x и t;

- процедуру вычисления интеграла по одной из квадратурных формул с формальными параметрами: границы интегрирования a, b, точность вычисления интеграла , функция F(x, t) и значение ее параметра t.

Исходные данные

I. Квадратурные формулы для вычисления интеграла (всюду ):

а) формула прямоугольников

;

б) формула трапеций

;

в) формула Симпсона ( n  четно)

.

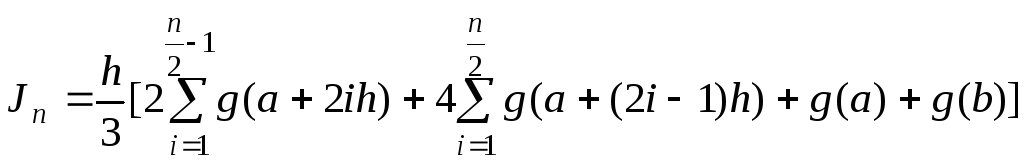За приближенное значение интеграла принимается такое, при котором .

II. Подынтегральная функция. Представим

.

Тогда функция  (x):

а) ; г) ;

б) ; д) ;

в) ; е) .

Функция  (z):

а) ; г);

б) ; д) ;

в) ; е) .

III. Числовые данные

	a	b		M	t1	t2	t3	t4	t5	t6
а)	0	1	0,1	3	-3,7	1,8	7,2	-	-	-
б)	-1	2	0,2	4	-2,1	-3,0	-0,9	1,8	-	-
в)	0,8	2,6	0,3	5	-0,6	-0,1	0,3	1,9	7,8	-
г)	-2	0	0,3	6	-2,6	-1,8	-0,2	0,7	1,6	2,5
д)	1	4	0,2	3	-0,4	2,6	7,9	-	-	-
е)	3,0	3,7	0,1	4	-1,6	-1,5	-1,4	1,4	-	-

1.2 Табулирование неявной функции.

Вычислить приближенно значение функции в заданных точках x₁,…, x_n, если функция задана уравнением F(x, y) = 0. Точность вычисления . Входными данными программы являются числа n,  и массив x[1: n];выходные данные  пары чисел (x_i, y_i), i = 1, …, n такие, что F(x_i, y_i) = 0. Корень уравнения F(x_i, y_i) = 0 находится одним из итерационных методов.

В программе предусмотреть:

- процедуру-функцию, вычисляющую значение F(x, y), с формальными параметрами x и y;

- процедуру нахождения корня уравнения F(a, y) = 0 итерационным методом.

Исходные данные

I. Итерационный метод нахождения корня уравнения F(a, y) = 0:

а) Метод касательных. При заданном начальном приближении корня y₍₀₎ по формуле

находятся очередные приближения до тех пор, пока не окажется

Тогда y_(k) = y* принимается за искомое значение корня.

Формальными параметрами процедуры нахождения корня должны быть: начальное приближение корня y₍₀₎, точность приближения , функции F(x, y), F (x, y) и значение параметра x.

б) Метод половинного деления отрезка. При заданных начальных границах интервала и , содержащего искомый корень, итерационным процессом вычисляются новые границы по границам :

• вычисляется ;

• если 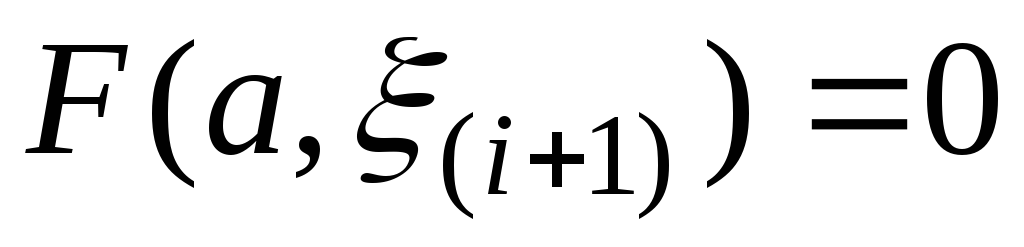, то искомый корень ;

• если , то ;

• если , то

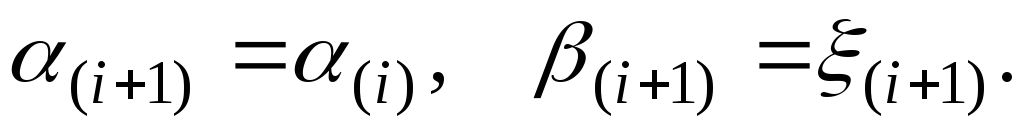
Итерации проводятся до тех пор, пока на некотором шаге не окажется ; тогда принимается за искомое значение y*.

Формальными параметрами процедуры нахождения корня должны быть: начальные границы , , точность приближения , функция F(x, y) и значение ее параметра x.

в) Метод хорд. Этот метод отличается от предыдущего только тем, что точка определяется другим выражением

.

II. Исходную функцию F(x, y) зададим в виде:

F(x, y) = yf (x) + g (x) +h (y).

В качестве начального приближения выбрать (для x = a)

.

В качестве начальных границ выбрать (для x = a)

.

Функция F (x, y) = f (x) + h (y)

Варианты задания функции g (x):

а) ; г) ;

б) ; д) ;

в) ; е) .

Варианты задания функции f (x):

а) 3 + 2x²; г) 10,8  x ;

б) 6 + 9 x; д) 1,7x² + 1;

в) 2x²  x + 1,8; е) (1 + 0,6x)².

Варианты задания функции h (y) и h (y):

а) h (y) = 2,7 sin y; h (y) = 2,7 cos y;

б) h (y) = 1,14 cos² y; h (y) = 1,14 sin 2y;

в) h (y) = 0,2 e ^–y2 ; h (y) = 0,4ye ^y2;

г) h (y) = ; h (y) = .