Раздел 4

Раздел 4

4.1 << Математические приемы анализа и обработки результатов эксперимента >>

Различают следующие виды экспериментов:

1. Реальные – опыты, проводимые в действительности в конкретных экспериментальных условиях.

2. Физические – опытные изучения свойств материальных объектов и явлений (подразумевают под собой проведение физического моделирования)

Математические приемы анализа и обработки результатов эксперимента

1. Физическое моделирование

2. Математическое моделирование – объекты создаются виртуально.

3. Метод аналогии – когда невозможно или технически сложно провести эксперимент с реальными физическими объектами

Физическое моделирование:

• Полное – моделирование проходит в натуральных величинах и испытание протекает в реальных условиях.

• Частичное – объект исследования создается не полностью; создается часть, наиболее интересная исследователю; условия могут быть различны.

Модель физического моделирования может иметь реальный масштаб или +/-

Пример физической модели: двигатель автомобиля

Математическое моделирование:

• Аналоговое – один из важнейших видов моделирования, основанный на аналогии явлений, имеющих различную физическую природу, но описываемых одинаковыми математическими (дифференциальными, алгебраическими или какими-либо другими) уравнениями.

Пример аналогового моделирования — две системы, первая из которых имеющая механическую природу, состоит из оси, передающей вращение через пружину и маховик, погруженный частично в вязкую тормозящую жидкость, валу, жестко связанному с маховиком. Вторая система — электрическая — состоит из источника электродвижущей силы, соединённого через катушку индуктивности, конденсатор и активное сопротивление со счётчиком электрической энергии. Если подобрать значения индуктивности, ёмкости и сопротивления так, чтобы они определённым образом соответствовали упругости пружины, инерции маховика и трению жидкости, то эти системы обнаружат структурное и функциональное сходство (даже тождество), выражаемое, в частности, в том, что они будут описываться одним и тем же дифференциальным уравнением.

Другой традиционной областью применения является исследование процессов теплопроводности.

• Численное – решается при помощи компьютера

Метод аналогии

Строится физическая модель, в которой процессы проходят на основе других физических законах и принципах и на основе тех же математических взаимосвязей.

Пример метода аналогии – физический процесс распространения тепла и движение вещества описываются теми же законами, что и электрические процессов.

Это применение не имеет большого распространения.

4.2 << Способы проверки полученных результатов >>

При проведении экспериментов любого вида вне зависимости от всего нет гарантии получения недостоверности результатов

Проверка на промахи

Доверительный интервал

???????????????????????????

4.2 << Математическая обработка результатов эксперимента >>

Неотъемлемой составляющей любого экспериментального исследования является оценка измерений.

Вследствие неточности измерительных приборов, несовершенства органов чувств человека, неполноты знаний, трудности учета побочных явлений при повторении одного и того же измерения получаются разные числовые значения измеряемой величины.

При практическом использовании результатов тех или иных измерений возникает вопрос о точности измерений, то есть степени приближения результатов измерения к некоторому действительному значению. Для количественной оценки используется понятие «погрешность измерений» или «ошибка».

Результат каждого прямого измерения включает случайную ошибку, которая зависит от большого числа случайных факторов. Если отклонения, вызываемые этими факторами, по абсолютной величине меньше чувствительности прибора, то они не обнаруживаются. В этом случае критерием точности измерения является цена наименьшего деления шкалы прибора или ее половины.

Методика

 При  измерениях одной и той же величины получаются результаты 

Среднее арифметическое из этих результатов

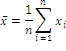
есть величина, наиболее близкая к истинному значению, которую называют средним значением. Следовательно, каждое измерение должно быть повторено несколько раз. В теории погрешностей доказывается, что при увеличении числа   среднее арифметическое стремится к истинному значению измеряемой величины.

Разности между средним значением   измеряемой величины и значениями  , полученными при отдельных измерениях называются абсолютными ошибками

и могут быть как положительными, так и отрицательными. Для определения средней абсолютной ошибки результата берут среднее арифметическое абсолютных значений отдельных ошибок, то есть

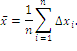
Отношения

называют относительными ошибками отдельных измерений.

Отношение средней абсолютной ошибки результата к его среднему значению дает среднюю относительную ошибку результата измерений: 

Принято относительные ошибки выражать в процентах 

Истинное значение измеряемой величины находится в интервале

Оценка точности и правильности при малом числе измерений [5].

количество измерений 

Единичные отклонения — отклонения отдельных измерений от среднего арифметического (абсолютная ошибка единичного измерения) 

Алгебраическая сумма одиночных отклонений равна нулю 

Выборочная дисперсия для n найденных значений   случайной величины:

Положительные значения корня квадратичного из дисперсии называется средней квадратической ошибкой отдельного измерения или выборочным отклонением:

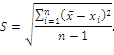
При оценке точности полученных результатов вычисляют также выборочную дисперсию среднего значения (среднего результата):

Средней квадратической ошибкой среднего арифметического или стандартным отклонением среднего результата:

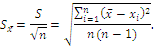
Доверительный интервал при заданной доверительной вероятности зависит от размера выборки, т.е. от количества проведенных опытов. В общем случае граница доверительного интервала при выбранном коэффициенте надежности  выражается уравнением:

где:   коэффициент Стьюдента.

Абсолютная ошибка: 

Коэффициент Стьюдента   с надежностью   показывает во сколько раз разность между истинным и средним результатами больше стандартного отклонения среднего результата:

Относительную ошибку среднего результата вычисляют с надежностью   по формуле:

Таким образом, значения  полностью определяет точность (воспроизводимость и правильность) измерений.

4.4 << Графический анализ >>

Обладает большой простотой,наглядностью. При небольших затратах труда графический способ позвляет быстро получить решение многих задач. В сравнение с математическим способом обладает невысокой точностью и становится затруднительно им пользоваться при больших количествах переменных.

Графический анализ используют в предварительной обработке данных, для выявления качественных закономерностей исследуемого явления, для иллюстрации результатов математического анализа и представления полученных результатов.

Для графического анализа важно правильно выбрать масштаб координат осей: при слишком маленьком масштабе зависимость сама не проявится; при слишком большом масштабе начинает проявлять себя случайная погрешность.

Для координатных осей размер шкал должен быть выбран такой, чтобы цена наименьшего деления примерно соответствовала значению средне квадратичной погрешноти исследуемой величины.