Метод аналогий

1.Метод аналогий

Из лекций

Моделирование методом аналогий.

В случае когда невозможно или сложно привести эксперисент с реальными физическими объектами строют физ. Модель, в которой процессы происходят на основе других физ. Законах и принципах, но на основе тех же математических взаимосвязей, например, физ. Процесс распространения теплого движения вещества описываются теми же самыми законами, что и процессы электрические.

Применение модели методом аналогий не имеет широкого применения в силу того что другие методы более доступны( в основном численное математическое моделирование)

Из интернета

Физические системы или явления могут быть сходны, похожи, аналогичны как по своему поведению, так и по математическому их описанию. Например, сжатый под поршнем газ иногда ведет себя аналогично упруго деформированной пружине, и, возможно, рассматривая малые колебания поршня, следует помнить о колебаниях груза на пружине?

Метод аналогии дает возможность сформировать понятный образ нового явления, а значит, способствует упрощению и его математического описания.

Часто изучая новые разделы физики, будь то термодинамика или электростатика, оптика или ядерная физика, помогаем себе, наводя переправу к уже изученному, подыскивая физические аналогии. Это преимущественно аналогии механические и касаются они механических или немеханических процессов. Но бывает и наоборот, когда удается найти немеханическую аналогию механическим процессам.

Из методички

Метод аналогий применяют в случае, когда удается подобрать процесс, существенно легче осуществляемый экспериментально, чем натурный, и когда экспериментальные измерения проводят с большей точностью, чем в натурных условиях. Так, для исследования температурных полей в твердых телах и неподвижных жидкостях широкое распространение получили электрические модели (электроинтеграторы). Решение таких задач в строгой математической постановке осуществляется с использованием ЭВМ. На электрических моделях можно получить предварительные сведения об изучаемых полях. Результаты измерений можно также использовать в итерационных расчетах на ЭВМ в качестве первого приближения.

2. Понятие о методе и виды аналогий используемых в научных исследованиях

Виды аналогий используемых в научных исследованиях:

Электротепловая аналогия, Электрогидравлическая аналогия, диффузионно-тепловая аналогия

3.Электротепловая аналогия

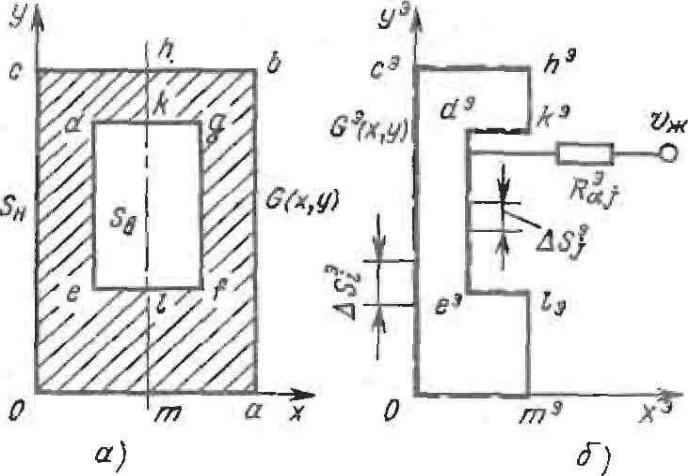
Электротепловая аналогия (ЭТА) - экспериментальный метод решения уравнений теплопроводности, осуществляемый на электрических моделях. Наиболее распространены модели для решения стационарных двумерных задач, в которых теплопроводящая область заменяется геометрически подобной областью из графитизированной бумаги или металлической фольги (рис, 5.1). В электрической модели измеряется распределение электрических потенциалов v и токов /, а по ним путем пересчета находят распределение температуры и тепловых потоков Q. Пересчет осуществляется на основе применения третьего правила подобия к уравнениям тепло- и электропроводности в неподвижной среде.

Задание температуры на границах теплопроводящей области имитируется заданием электрических потенциалов на соответствующих границах электропроводящей области. На эти участки накладываются электрические шины. Конвективный теплообмен между поверхностью тела и рабочей жидкостью, характеризуемый коэффициентом термического сопротивления теплоотдачи Rx имитируется протеканием электрического тока по электрическим сопротивлениям Rэ x, присоединенным к соответствующим участкам контура модели.

Рис. 5.1. Электромоделирование стационарного поля температуры в стенках канала:

а) область поперечного сечения канала,

G(х, у) с симметрией по оси h-m;

SН и SB — наружный и внутренний контуры;

б) — электропроводная область

G’ [х. у); i и j - номера участков Sэj; и Sэj с наложенными шинами; vж = vминi- электрический потенциал, соответствующий температуре Тж

Электрогидродинамическая аналогия (ЭГДА) - экспериментальный метод решения задач гидродинамики на электрических моделях. Наиболее распространены модели для исследования обтекания тел плоским двумерным безвихревым потоком идеальной жидкости, в которых область течения заменяется графитизированной бумагой. Модель обтекаемого тела выполняется с соблюдением геометрического подобия либо в виде выреза в проводящей бумаге (1-й метод), либо из хорошего электрического проводника (2-й метод). По первому методу используется аналогия между распределением электрических потенциалов v и потенциалов скорости , по второму — между распределением v и функцией тока Для сходственных точек выполняются равенства (равенство вам завтра напишу, не копируется в ворд),где - измеряемая разность электрических потенциалов по отношению к потенциалу одной из шин; — разность потенциалов между шинами; и — минимальные величины на границах области течения, которые в силу произвольного выбора начала отсчета для и принимаются равными нулю; — скорость набегающего потока. На модели измеряется распределение величин V = Ф (по первому методу) или V = Ч* (по второму методу). По методу ЭГДА можно найти распределение скорости при стабилизованном течении вязкой жидкости в каналах сложного поперечного сечения, а также коэффициенты сопротивления трения