
Раздел 2
.docxПогрешность измерений- отклонение результатов измерений физ. Величины от его истинного значения.
Результат измерений – оценка истинного значения измеряемой величины, которая, как правило, с ним не совпадает (погрешность).
Доверительный интервал – характеризует погрешность с определенной степенью достоверности.
Абсолютная погрешность – равна модулю разности между оценкой истинного значения и границей интервала (полуширина доверительного интервала).
Относительная погрешность- это частное от деления абсолютной погрешности на модуль приближенного значений измеряемой величины.
Классы погрешностей
По форме представления
Абсолютная погрешность
Относительная
погрешность — погрешность измерения,
выраженная отношением абсолютной
погрешности измерения к действительному
или среднему значению измеряемой
величины (РМГ 29-99): ![]() ,
, ![]() .
.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
По причине возникновения
Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
![]() а=К*А/100
а=К*А/100
Прецизионные классы точности К=0,05; 0,1; 0,2; 0,5
Технические К=1,0; 1,5; 2,5; 4,0
Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
По характеру проявления
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью
![]() =t*S
, S – среднее квадратичное
значение
=t*S
, S – среднее квадратичное
значение
Грубая погрешность (промах) – погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных значений погрешности. Грубые погрешности необходимо всегда исключать из рассмотрения, если известно, что они являются результатом очевидных промахов при проведении измерений.
Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
По способу измерения
Погрешность прямых измерений — вычисляется по формуле
![]()
где : ![]() ;
; ![]() —
стандартная ошибка среднего (выборочное
СКО, деленное на корень из количества
измерений
—
стандартная ошибка среднего (выборочное
СКО, деленное на корень из количества
измерений ![]() ),
а
),
а ![]() — квантиль
распределения Стьюдента для
числа степеней свободы
— квантиль
распределения Стьюдента для
числа степеней свободы ![]() и
уровня значимости
и
уровня значимости ![]() ;
; ![]() —
абсолютная погрешность средства
измерения (обычно это число, равное
половине цены деления измерительного
прибора).
—
абсолютная погрешность средства
измерения (обычно это число, равное
половине цены деления измерительного
прибора).
Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если ![]() ,
где
,
где ![]() —
непосредственно измеряемые независимые
величины, имеющие погрешность
—
непосредственно измеряемые независимые
величины, имеющие погрешность ![]() ,
тогда:
,
тогда:
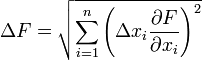
Погрешность косвенных невоспроизводимых измерений — вычисляется аналогично вышеизложенной формуле, но вместо ставится значение полученное в процессе расчётов.
3. Показатели точности и формы
представления результатов эксперимента
В соответствии с ГОСТ 8.011-72 устанавливаются
следующие показатели
точности измерений:
- интервал, в котором погрешность
измерения находится с заданной
вероятностью;
- интервал, в котором систематическая
погрешность измерения находится с
заданной вероятностью;
- числовые характеристики систематической
составляющей погрешности измерения;
- числовые характеристики случайной
составляющей погрешности измерения;
- функция распределения или плотность
вероятности систематической составляющей
погрешности измерения;
- функция распределения или плотность
вероятности случайной составляющей
погрешности измерения.
Формы представления результатов измерений
Общая форма представления результата измерения в соответствии с требованиями МИ 1317–86 включает:
точечную оценку результата измерения;
характеристики погрешности результата измерения (или их статистические оценки);
указание условий измерений, для которых действительны приведенные оценки результата и погрешностей. Условия указываются непосредственно или путем ссылки на документ, удостоверяющий приведенные характеристики погрешностей.
В качестве точечной оценки результата измерения при измерении с многократными наблюдениями принимают среднее арифметическое значение результатов рассматриваемой серии.
Характеристики погрешности измерений можно указывать в единицах измеряемой величины (абсолютные погрешности) или в относительных единицах (относительные погрешности).
Характеристики погрешностей измерений или статистические оценки по НД:
среднее квадратическое отклонение погрешности;
среднее квадратическое отклонение случайной погрешности;
среднее квадратическое отклонение систематической погрешности;
нижняя граница интервала погрешности измерений;
верхняя граница интервала погрешности измерений;
нижняя граница интервала систематической погрешности измерений;
верхняя граница интервала систематической погрешности измерений;
вероятность попадания погрешности в указанный интервал.
Рекомендуемое значение вероятности Р = 0,95.
Требования к оформлению результата измерений:
наименьшие разряды должны быть одинаковы у точечной оценки результата и у характеристик погрешностей;
характеристики погрешностей (или их статистические оценки) выражают числом, содержащим не более двух значащих цифр, при этом к оставляемой цифре второго разряда добавляется единица, если последующая (отбрасываемая) цифра неуказываемого младшего разряда больше нуля;
допускается характеристики погрешностей (или их статистические оценки) выражать числом, содержащим одну значащую цифру, при этом к цифре первого разряда добавляется единица (округление в большую сторону) если цифра неуказываемого младшего разряда равна или больше 5, а при цифре меньше 5 округление осуществляется в меньшую сторону.
Оценка погрешности прямых измерений
http://akspa.narod.ru/Pogreshn.2003.pdf
Обратная задача теории
экспериментальных погрешностей.
Прямая задача в теории погрешностей заключается в определении погрешности результата по известным погрешностям исходных данных.
Обратная задача теории погрешности заключается в определении погрешностей исходных данных для обеспечения результата с заранее заданной точностью.
Целью обратной задачи является определение погрешностей величин-аргументов, если известны погрешность функции и вид функциональной зависимости.
Необходимость в решении таких задач возникает при выборе того или иного комплекта измерительной аппаратуры или метода определения искомой величины, позволяющих найти значение этой величины с определенной погрешностью.
28), обратная задача в общем случае является неопределенной, поскольку имеется «дно уравнение и п + т неизвестных.
Иначе говоря, удовлетворить условию задачи можно при различных комбинациях значений погрешностей аргументов.
Определение наивыгоднейших условий эксперимента
Под наивыгоднейшими условиями эксперимента понимаются такие условия, для которых погрешность результата эксперимента при фиксированном значении доверительной вероятности имеет наименьшее значение.
Следует заметить, что не всегда условия проведения эксперимента могут быть выбраны исходя из требований получения наиболее высокой точности результата. Часто эти условия выбираются из других соображений, например, необходимости исследования режимов, имеющих место в натурных объектах, и т.д.
