OTIP

где βi – безразмерный коэффициент влияния i-го звена:

С учетом (9.86) дисперсия суммарной погрешности (9.85) равна

3) пользуясь методом неопределенных множителей Лагранжа λ, составить функционал

4) исследовать на экстремум функционал F, для чего приравнять нулю частные производные

5) решить полученную систему n + 1 уравнений (9.90) с учетом условия равенства чувствительности прибора заданному значению (9.84). При решении

исключается λ, и определяются оптимальные значения Si опт , i =1, n ;

6) определить минимальное значение Dmin путем подстановки в (9.87) найденных оптимальных значений Si опт .

Общая чувствительность схемы является функцией чувствительности отдельных звеньев, причем вид этой функции зависит от их соединения.

При последовательном соединении звеньев:

Следовательно, в соответствии с (9.85) и (9.91) дисперсия погрешности последовательно соединенных звеньев равна сумме дисперсий отдельных элементов

n

D = ∑Di .

i=1

Таким образом, при последовательном соединении линейных звеньев минимизация случайных погрешностей за счет перераспределения чувствительности звеньев не представляется возможной. Уменьшение дисперсии можно добиться либо за счет повышения точности отдельных звеньев (уменьшение Di), либо за счет упрощения схемы (уменьшения числа звеньев n). Возможности уменьшения дисперсии погрешностей элементов ограничены,

151

поэтому дисперсия приборов прямого преобразования с последовательным соединением звеньев оказывается значительной. В этом основной недостаток приборов прямого преобразования.

При параллельном соединении:

Запишем выражение для дисперсии погрешности согласно (9.85) с учетом (9.92)

Если общая чувствительность задана ( S = S* ), то можно записать

При этом добавочное условие (9.84) имеет вид

n

ϕ = S* − ∑Si = 0. (9.95)

i=1

Составим функционал F, подставив в (9.88) выражения (9.93) с учетом (9.94) и (9.95),

Дифференцируя F по Si и приравнивая нулю частные производные, получим n алгебраических уравнений

Решая совместно систему уравнений (9.97) и (9.95), найдем оптимальные значения чувствительности звеньев прибора

Для определения минимальной дисперсии при параллельном соединении звеньев подставим значения Sm опт, m =1, n (9.98) в выражение (9.87) для дисперсии. После преобразований получим

Таким образом, при параллельном соединении звеньев и обеспечении оптимальных значений их чувствительности общая дисперсия меньше дисперсии любого звена, т. е. при оптимальном распределении чувствительности

152

измерительный прибор обладает более высокой точностью (в смысле случайной погрешности), чем любое звено, входящее в его состав. Это позволяет строить высокоточные измерительные цепи из компонентов с ограниченной точностью.

В частном случае при использовании n одинаковых преобразователей

Дифференцируя выражение для дисперсии (9.101) по k0 и приравнивая нулю, найдем

k0 = D1 D2 .

Итак, введение отрицательной обратной связи целесообразно в тех случаях, когда точность обратного преобразователя намного выше точности преобразователя прямой цепи.

Найдем оптимальные значения чувствительности звеньев:

При этом минимальная дисперсия определяется согласно (9.87) аналогично случаю параллельного соединения звеньев

9.10. Синтез приборов по критериям динамической точности

Измерительные приборы, работающие в динамическом режиме, имеют динамические погрешности. Синтез оптимальных характеристик таких приборов преследует цель минимизировать эти погрешности.

Для общности рассуждений будем считать, что прибор является сложной системой, имеющей матричную передаточную функцию. Введем следующие

153

идеального прибора размерности N × N ; W( p) = Wi j – матричная передаточная

функция реального (синтезируемого) прибора размерности N × N .

Синтез характеристик прибора проведем в два этапа: синтез структуры и синтез параметров, пользуясь в обоих случаях теорией приближения функций.

Синтез структуры прибора. При синтезе структуры прибора теория приближения функций строится на операциях с порядками полиномов передаточных функций.

Рассмотрим последовательность действий для достижения поставленной цели. 1. Представить элементы матриц W*( p), W( p) в виде дробно-рациональных

mi j , n.

Причем, степени полиномов числителей должны быть равны или ниже степеней полиномов знаменателей. Порядки полиномов характеризуют сложность структуры приборов, поэтому, синтезируя простую передаточную функцию, мы синтезируем прибор с простой (несложной) структурой.

2. Выбрать критерий близости передаточных функций реального и идеального приборов.

Условия наилучшего (точного) приближения передаточных матриц W*( p) и W( p) можно представить в виде

где Ω ={(i1, j1), (i2 , j2 ), ..., (ik , jk )} – подмножество, точками которого являются k

пар индексов (i, j) приближаемых функций. После подстановки (9.102) в(9.103) получается

Из выражения (9.106) следует, что наилучшее приближение функций Wi*j ( p) и Wi j ( p) достигается за счет компенсации части полюсов функции Wi j ( p) ее нулями, причем

154

Эти уравнения связывают искомые параметры синтезируемого прибора с известными параметрами идеального прибора.

4.Приравнять коэффициенты при соответствующих степенях p полиномов в левых и правых частях уравнений (9.107).

5.На основе (9.107) получить следующее количество алгебраических уравнений (КУ), связывающих параметры приборов:

6. Найти количество неизвестных параметров (КП) реального прибора, подлежащих определению из уравнений (9.107):

Для определенности системы уравнений (9.107) необходимо, чтобы количество неизвестных параметров КП было равно или больше количества

8. Выбрать критерий оптимальности (функцию цели), характеризующий сложность структуры.

В качестве функции цели можно взять линейную форму вида

Таким образом, задача синтеза оптимальной структуры прибора формулируется следующим образом: найти такие неотрицательные целочисленные значения неизвестных n и mi j , которые удовлетворяют

неравенствам (9.111) и (9.113) и минимизируют критерий оптимальности (9.112).

155

Эта задача решается методами линейного программирования, причем полученные значения n и mi j округляются до ближайших целочисленных

значений.

Синтез параметров прибора.

Задача синтеза параметров прибора, работающего в динамическом режиме, формулируется следующим образом: при выбранной структуре синтезируемого прибора и заданных характеристиках идеального прибора необходимо найти коэффициенты передаточных функций при условии минимума динамической погрешности

где ai, bj (i =1, n ; j =1, m ) – коэффициенты, зависящие от параметров синтезируемого прибора; ck, dl ( k =1, r ; l =1, ν) – коэффициенты идеального прибора.

Синтез параметров будем проводить при выполнении условий физической реализуемости

Рассмотрим методы решения этой задачи: метод разложения в ряды и метод деления полиномов передаточных функций.

1.Метод разложения в ряды. Разложим функцию динамической погрешности

вряд Маклорена по степеням p

156

Если передаточные функции имеют вид (9.115), (9.1116), то уравнения (9.121) запишутся в следующем виде:

2. Метод деления полиномов.

В передаточных функциях Wi j ( p) , Wi*j ( p) разделим полиномы числителей на полиномы соответствующих знаменателей и результат представим в виде:

В соответствии с условием точного приближения (9.103), реализующим условие минимума динамической погрешности (9.114), знаменатели в выражениях (9.123), (9.124) должны быть равны

Приравнивая коэффициенты при соответствующих степенях p полиномов в левых и правых частях выражения (9.125), получим систему алгебраических уравнений (9.122) для определения неизвестных параметров прибора.

Уравнения (9.122) можно получить также из условия приближения

путем приравнивания коэффициентов при одинаковых степенях p полиномов числителя и знаменателя.

Пример 9.4. Дана передаточная функция синтезируемого прибора

которую нужно приблизить к передаточной функции идеального прибора

157

После сравнения коэффициентов при одинаковых степенях p полиномов числителя и знаменателя получим:

Если динамическая система, описываемая согласно (9.127), содержит не менее четырех независимых параметров, то можно осуществить точное приближение. Решение системы уравнений (9.129) позволяет получить искомые параметры.

9.11. О синтезе приборов по нескольким критериям

При проектировании измерительных приборов необходимо не только минимизировать погрешности, но также уменьшить стоимость, увеличить чувствительность, надежность, уменьшить массо-геометрические характеристики. А значит, необходимо ввести комплексный критерий оптимальности, учитывающий несколько критериев.

Например, стоимость прибора, состоящего из n элементов, может быть функцией вида

где Di, Si, Mi, Pi – соответственно дисперсия погрешности, чувствительность, масса, надежность элемента номер i; Z0 – стоимость вспомогательных элементов, сборки и регулировки прибора, принимаемая постоянной.

Допустим, что составлены уравнения, связывающие одноименные характеристики элементов системы в виде:

Задача заключается в минимизации функции (9.130), как функции указанных переменных при дополнительных условиях (9.131).

158

Поставленная задача – это задача на условный экстремум функции нескольких переменных, которая может быть решена методом множителей Лагранжа. Согласно методу вводится в рассмотрение функция

m

Φ = Z + ∑λk ϕk , (9.132)

k =1

где λk – множители Лагранжа, количество которых равно количеству уравнений

вида (9.131), которые называются уравнениями связи. Далее, согласно методу, для нахождения минимума функции Ф составляют уравнения:

Присоединяя к системе n·m уравнений (9.133) m уравнений связи вида (9.131) и решая полученную систему (n·m + m) уравнений относительно того же количества неизвестных переменных и множителей Лагранжа, получаем экстремальные значения переменных.

10. ОЦЕНКА ВЛИЯНИЯ ПРОИЗВОДСТВЕННОТЕХНОЛОГИЧЕСКИХ ПОГРЕШНОСТЕЙ

НА РЕАКЦИИ ГИДРОДИНАМИЧЕСКОГО ПОДВЕСА МИНИАТЮРНОГО ШАРОВОГО ГИРОСКОПА

Рассматриваемая задача относится к проблеме создания современных миниатюрных систем инерциальной навигации и управления движением объектов различного назначения. Разработка перспективных навигационных систем предполагает создание гироскопических датчиков, обладающих малой массой и габаритами, низкими себестоимостью и энергопотреблением, достаточно высокой надежностью. Проблема миниатюризации тесно связана с задачей оценки точности таких устройств.

Ряд вариантов реализации таких датчиков содержит в своей основе

миниатюрный шаровой гироскоп в гидродинамическом подвесе [4]. Пример применения такого гироскопического датчика представлен на рис. 10.1.

159

Д1

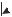
Рис. 10.1. Функционально-кинематическая схема двухосного гиростабилизатора

Ротор шаровой формы, представляющий собой постоянный двухполюсный магнит, заключен в заполненную маловязкой немагнитной жидкостью сферическую полость каркаса статора, сообщающуюся через отверстия с камерой, в которой жидкость находится под давлением. Величина зазора между поверхностями ротора и полости в радиальном направлении мала по сравнению с радиусами каждой из поверхностей. Ротор приводится в быстрое вращение магнитным полем электрических обмоток 1, 5, расположенных на каркасе статора (см. рис. 10.1). Прибор, включающий в себя датчик угла 4, датчик момента 3 и синхронизирующие обмотки 2, 6, может служить чувствительным элементом гиростабилизатора. Сигналы с датчика угла 4 и синхронизирующих обмоток 2, 6 подаются на усилительно-преобразовательный блок (УПБ), с помощью которого формируются сигналы Uα,Uβ управления двигателями стабилизации Д1, Д2.

Датчик момента 3 используется для компенсации постоянных составляющих возмущающих моментов и для начальной выставки платформы. Сферический гидродинамический подвес создает возможность центрирования ротора и демпфирования колебаний его главной оси и обладает большой несущей способностью.

Уравнения относительного движения шарового гироскопа – чувствительного элемента гиростабилизатора в первом приближении в проекциях на оси Резаля можно записать в виде:

160