МММСС (От Кувыркина Г.Н.) / 99

1

2. Основные модели газовой динамики

Газовая динамика — раздел механики жидкости и газа, в котором изучают движение сжимаемой сплошной среды с большой скоростью и ее взаимодействие с твердыми телами. Малая пространственная протяженность области взаимодействия газового потока с твердым телом позволяет отбросить в уравнениях газовой динамики объемные силы, а большая скорость движения требует учета сжимаемости рассматриваемой среды.

При большой скорости движения вязкость газа не играет существенной роли и область ее влияния ограничивается сравнительно тонким пограничным слоем. За пределами этого слоя движение газа может быть описано математической моделью, содержащей уравнения движения идеальной сжимаемой жидкости, но без учета объемных сил. Поскольку термин «идеальный газ» часто используют как синоним термина совершенный газ, чтобы избежать путаницы, для краткости вместо идеальной или вязкой сжимаемой жидкости в этой главе будем говорить о невязком или вязком газе соответственно.

Наличие большой скорости движения отличает газовую динамику от других областей механики сжимаемой жидкости (таких, как акустика или метеорология) возможностью образования поверхностей, при переходе через которые параметры потока претерпевают разрыв. Наличие таких поверхностей заставляет с осторожностью подходить к построению математических моделей. При очень больших скоростях за поверхностью разрыва температура потока может достигать весьма больших значений, возможна диссоциация молекул газа на атомы или на молекулы с меньшим числом атомов, а при еще б´ольших температурах — ионизация, связанная с утратой атомами или молекулами газа электронов. Указанные особенности выделяют газовую динамику в отдельный раздел механики жидкости и газа.

2.1. Дифференциальная форма модели газовой динамики

Состояние движущегося в области V невязкого газа в произвольный момент времени t характеризуют локальные значения его плот-

ности ρ, давления p, массовой плотности внутренней энергии u и

проекций vi (i = 1, 2, 3) вектора v скорости на оси Oxi прямоугольной декартовой системы координат. Дифференциальная форма математической модели газовой динамики включает уравнение неразрывно-

2

сти (закон сохранения массы) в дивергентной форме

уравнения движения (закон сохранения количества движения сплошной среды) в дивергентной форме

символ Кронекера) и не учитывается влияние плотности объемных сил (bi ≡ 0), и уравнение закона сохранения энергии в виде

плового потока, qV — объемная плотность мощности внутренних источников теплоты и мощности bivi объемных сил.

Условия на поверхности разрыва S , которая может возникнуть при движении газа, согласно (1)–(3), имеют вид

где Dn = D · n > 0 — проекция вектора D скорости движения произвольной точки M S на направление вектора n вектора нормали к поверхности S , имеющего проекции ni на координатные оси Oxi; [ ·] — скачок соответствующей величины в этом направлении. Если перейти к системе координат, связанной с этой точкой и движущейся со скоростью D , то вместо (4) получим

[ρv˜i] n = 0, [ρviv˜j + pδij] n = 0, hρ vivi + u v˜j + pvjin = 0, (5)

i j 2 j

где v˜j — проекции вектора v˜ = v − D скорости частиц газа на оси подвижной системы координат.

При адиабатическом процессе движения газа и отсутствии объемных источников энерговыделения исследуемый процесс можно рассматривать и как изоэнтропический, т. е. считать массовую плотность h

3

энтропии постоянной, положив h = 0. Поэтому u можно отождествить с массовой плотностью A свободной энергии и записать

где cv — удельная массовая теплоемкость при постоянном объеме; T — абсолютная температура газа. Тогда при cv = const третье уравнение (5) примет вид [ρ(vivi/2 + cvT )˜vj + pvj]nj = 0.

так как справедливы уравнения Эйлера при bi ≡ 0. Далее, полагая газ совершенным, уравнение состояния которого имеет вид

где Rg = Rµ/µg — газовая постоянная; Rµ — универсальная газовая постоянная; µg — молекулярная масса газа, и используя (1) в виде

Отсюда при cv = const получим T/ρκ−1 = const, где κ = cp/cv — показа-

тель адиабаты, а cp = cv + Rg — удельная массовая теплоемкость газа при постоянном давлении, или изобарная теплоемкость,

соответствующая изобарному (при постоянном давлении газа) термодинамическому процессу. Тогда с учетом (8) получаем уравнение

адиабаты Пуассона

Таким образом, для изоэнтропического процесса движения газа p в силу

(9) зависит лишь от ρ. В этом случае газ называют баротропным. Отметим, что всегда κ > 1. При нормальной температуре для одноатомного газа κ = 5/3, а для двухатомного газа κ = 7/5.

4

Если газ не является совершенным, т. е. его параметры не удовлетворяют (8), то в качестве уравнения состояния можно использовать

уравнение Ван–дер–Ваальса в виде

Кроме того, для реального газа следует также учитывать зависимость cv от T , которую можно задать в виде

Если для изоэнтропического процесса представить зависимость T от ρ

в виде T (ρ) = T (0)(ρ) + α1T (1)(ρ) + β1T (2)(ρ) + c1T (3)(ρ) + c2T (4)(ρ) и при-

нять коэффициенты α1, β1, c1, c2 малыми, а в дальнейшем пренебречь слагаемыми, содержащими произведения этих коэффициентов, то после интегрирования (11) найдем

начальном состоянии (например, в состоянии покоя).

В случае малости скорости v и ее производных, считая малыми и изменения p = p − p0 и ρ = ρ − ρ0 давления p и плотности ρ по сравнению с давлением p0 и плотностью ρ0 газа в его невозмущенном состоянии, из (1) и (2) с учетом (8) и (9) получаем

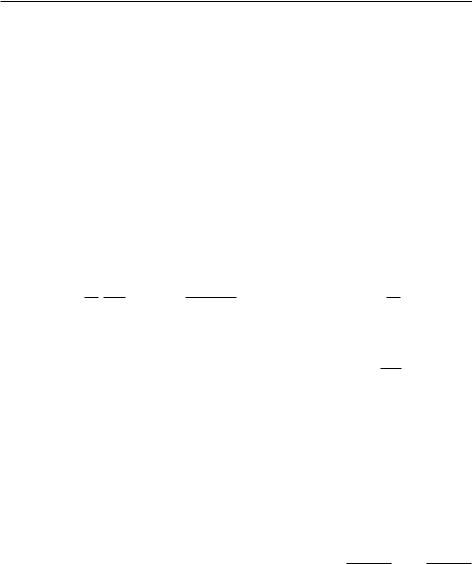
5

приближенные равенства точными, приходим к известным волновым уравнениям

описывающим распространение малых возмущений. Пространственную форму распространяющегося возмущения называют волной.

Если до возникновения возмущения плотности газа векторное поле скоростей обладало потенциалом Φ0(x,t), где x — радиус-вектор точ-

ки с пространственными координатами xi, то и при распространении малого возмущения это поле остается потенциальным. Действительно, из второго соотношения (13), полагая, что возмущение возникло в момент времени t = 0 и vi|t=0 = ∂Φ0(x,0)/∂xi, интегрированием по времени t получаем

потенциал поля скоростей газа в процессе распространения малого воз-

мущения плотности газа, удовлетворяющий уравнению ∂2Φ = a2 rx Φ.

∂t2 0

При установившемся движении невозмущенного газа потенциал Φ0 не зависит от времени t. В этом случае

Пусть в момент времени t = 0 в неподвижном газе плотностью ρ0

впределах шаровой области радиусом r0 возникает малое возмущение ρ плотности. Это возмущение в силу центральной симметрии поро-

ждает сферическую волну ρ(r,t) = ρ0 + ρ(r,t), распространение ко-

торой описывается первым уравнением (14) в виде

(r — расстояние от центра этой области). При этом потенциал Φ(r,t) поля скоростей будет удовлетворять аналогичному уравнению

6

Поскольку при r = 0 потенциал остается конечным, вместо последнего равенства следует записать

Используя начальные условия, (18) и (19) приведем к виду fΦ(−r) −

При t > 0 для точек за пределами возмущенной шаровой области a0t + + r > r0, т. е. аргумент функции fΦ0 (a0t + r) всегда больше r0. Поэтому для этих точек в силу (17) и (20) и fΦ0 (a0t + r) = a0(a0t + r)/2.

из (19) следует, что в первом и третьем промежутках ρ(r,t) = ρ0, т. е. газ остается невозмущенным, а во втором промежутке ρ(r,t) = ρ0 +

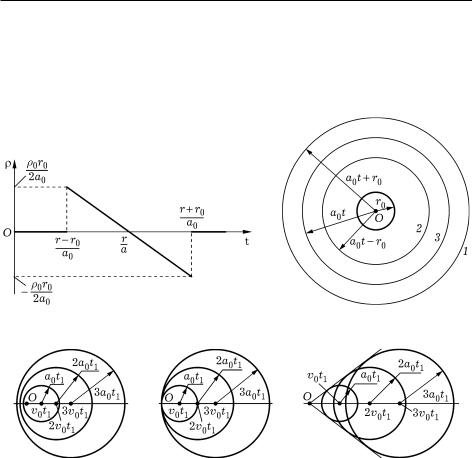
Изменение плотности газа в рассмотренных промежутках времени представлено на рис. 0.1, причем на границах этих промежутков плотность газа изменяется скачком. При фиксированном значении r изменение плотности происходит в течение промежутка времени 2r0/a0. В момент времени t > 0 передний фронт сферической волны (позиция 1 на рис. 0.2) достигает точек, расположенных на расстоянии r = a0t + r0 от центра O шаровой области начального возмущения плотности газа. При t > 2r0/a0 за пределами этой области формируется задний

7

фронт 2 сферической волны, который достигает точек, расположенных на расстоянии r = a0t − r0 от центра O, и эта волна располагается в сферическом слое толщиной 2r0, равномерно расширяющемся со скоростью a0. Сфера 3 радиусом r = a0t делит этот слой на внешнюю (ρ > ρ0) и внутреннюю (ρ < ρ0) части.

Рис. 0.3

В случае точечного источника возмущения r0 = 0 и шаровой слой переходит в сферическую поверхность, также равномерно расширяющуюся со скоростью a0. Если такой источник движется из начальной точки O прямолинейно с постоянной скоростью v0, то для неподвижного наблюдателя сферическая волна в различные моменты времени не будет представлять собой концентрические сферы. При v0 < a0 каждому моменту времени t1, 2t1, 3t1, . . . соответствует сфера, охватывающая все сферы для предшествующих моментов времени (рис. 0.3, а). В случае v0 = a0 все сферы имеют общую точку касания, соответствующую начальному положению точечного источника (рис. 0.3, б). При v0 > a0 все сферы касаются прямого кругового конуса (рис. 0.3, в), называемого конусом Маха. Вершина этого конуса совпадает с начальным положением источника, а полуугол arcsin(a0/v0) при вершине называют

углом Маха.

8

2.2. Одномерное течение невязкого газа

При установившемся одномерном течении невязкого газа в прямолинейном канале постоянного поперечного сечения из (1) следует ρv = const, где ρ — плотность газа, а v — модуль вектора скорости. Отсюда ρdv + v dρ = 0, или

Для такого течения из (2) получим ρv dv + dp = 0, где p — давление газа. Используя последнее равенство и (21), находим

При изоэнтропическом процессе движения газа dp/dρ, согласно (9),

является функцией только p или ρ. В этом случае (22) определяет скорость распространения в канале малого возмущения неизменной фор-

мы, удовлетворяющую как уравнению неразрывности, так и уравнению движения, называемую местной скоростью звука и обозначаемую через a. Для совершенного газа с учетом его уравнения состояния (8)

где Rg — газовая постоянная; T — абсолютная температура газа.

где cv = const — удельная массовая теплоемкость газа при постоянном объеме, или, учитывая (8) и (23),

тура торможения T0 = T + v2/(2cp) (cp — удельная массовая тепло-

емкость при постоянном давлении) и плотность ρ0 = p0/(RgT0).

Если в (25) положить v = a, т. е. приравнять скорость потока местной скорости звука, то получим значение критической скорости

Безразмерный параметр M = v/a, характеризующий влияние сжима-

Отсюда следует, что a < a при M < 1 и a > a при M > 1.

При изоэнтропическом процессе неустановившегося одномерного течения невязкого газа в прямолинейном канале постоянного поперечного сечения из (1), (2) и (9) имеем

где t — время; x — координата, отсчитываемая вдоль оси канала. Для малых отклонений p = p − p0 и ρ = ρ − ρ0 давления p и плотности ρ от соответственно давления p0 и плотности ρ0 газа в невозмущенном состоянии при малой скорости v и ее производных из (13) следуют одномерные волновые уравнения

10

общие решения которых имеют вид ρ(x,t) = fρ(x − a0t) + gρ(x + a0t) и v(x,t) = fv(x − a0t) + gv(x + a0t). Анализ этих решений показывает,

вправо и влево на расстояние a0t1. Вдоль линий x −a0t = const решения fρ(x − a0t) = const и fv(x − a0t) = const, а вдоль линий x + a0t = const

решения gρ(x + a0t) = const и gv(x + a0t) = const. Эти линии называют

характеристиками волнового уравнения.

Если возмущения скорости не являются малыми, то необходимо решать систему нелинейных уравнений (30), и, как правило, численно. В частном случае зависимости ρ только от v, т. е. ρ = f(v), удовлетворяющей первым двум уравнениям (30), с учетом третьего уравнения (30)

Непосредственной проверкой можно установить, что этим уравнениям удовлетворяют соотношения

где Fρ и Fv — произвольные функции.

При |v/a| → 0 соотношения (32) переходят в общие решения волновых уравнений (31). Из (32) следует, что в подвижной системе координат, начало которой имеет скорость v ±a, плотность и скорость частиц газа остаются постоянными. Отсюда можно сделать вывод, что возмущения будут распространяться со скоростью v ± a, в общем случае различной в разных точках потока газа, поэтому пространственная форма возмущений будет изменяться во времени.

= 0 волнообразное распределение возмущения скорости v вдоль оси Ox (рис. 0.4, а). Поскольку возмущения в области, где v > 0, распространяются быстрее, чем в области, где v < 0, то при t > 0 гребень волны будет стремиться нагнать впадину, что приведет к более резкому изменению скорости в зоне смены ее знака (рис. 0.4, б). В рамках