
8693
.pdf
2. Образцы вариантов билетов и их решений Вариант 1
1. Упростите до числового ответа выражение |
a + 1 |
|
|
|||||
a + 1 |
a3 + 1 |
+ a2 a + 1 |
|
5a |
|
|||
1 |
3 |
3 |
|
|
|
10a |
5 |
|
2.Свежие грибы содержат по весу 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 44 кг свежих?
1 x2+4x 271 x
4. |
Вычислите |
|
cos2 3 + cos2 cos 4 cos 2 |
|||||||
6. |
Решите неравенство |
(x 3) p2x 2 |
3 + px 1 = 2 (x 3) |
|||||||
5. |
Решите уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
(log3 3x) |
3 log3 x > 7 |
||||||
|
|
|
|
|
||||||
7. |
Дано уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 = ctgx cos x: |
|||||
|
|
|
|
|||||||
|
|
sin x |
||||||||
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
[0; 4 ].
8.В треугольнике ABC медиана AM делит биссектрису CK в отношении 5:3, считая от вершины C. Найдите отношение длин сторон треугольника AC è BC (большей к меньшей).
9.Найдите все значения параметра a, при которых система
уравнений (
log2 x + log2 y = 6; y = 8 + a(x 6)
11

имеет два различных решения.
Решение задач варианта 1.
Замечание. Тексты задач в чистовик можно не переписывать. Достаточно краткой записи условия.
1. Упростите до числового ответа выражение |
a + 1 |
|
|
|||||
a + 1 |
a3 + 1 |
+ a2 a + 1 |
|
5a |
|
|||
1 |
3 |
3 |
|
|
|
10a |
5 |
|
Решение.
1) |
1 |
|
|
|
3 |
|
+ |
|
3 |
|
|
= |
a2+2a+1 |
= |
(a+1)2 |
= |
a+1 |
|||
|
|
a+1 |
a3+1 |
|
a2 a+1 |
|
(a+1)(a2 a+1) |
(a+1)(a2 a+1) |
a2 a+1 |
|||||||||||
2) |
5a |
|
10a 5 |
= 5 (a2 a+1) |
|
|
|
|
|
|||||||||||
|
|
|
|
a+1 |
|
|
a+1 |
|
|
|
|
|
|
|||||||
3) |
|
a+1 |
|
|
5 (a2 a+1) |
= 5 |
|
|
|
|
|
|||||||||
|
|
a2 a+1 |
|
|
a+1 |
|
|
|
|
|
|
|||||||||
Ответ: 5
2.Свежие грибы содержат по весу 90% воды, а сухие 12% воды. Сколько получится сухих грибов из 44 кг свежих?
Решение. Свежие грибы содержат воду (90%) и вещество (10%). Сухие грибы содержат воду (12%) и вещество (88%). Процесс сушки грибов состоит в том, что вода испаряется, а
вещество остается. Согласно условию, 10% от 44 кг составляет 44 0;1 = 4;4 êã. Ýòè 4;4 кг составляют 88% вещества. Тогда
4;4 êã 88% x êã 100%
Отсюда, |
4; 4 100 |
|
|
x = |
= 5 êã: |
||
88 |
|||
|
|
Ответ: 5
12

3. |
Решение. ОДЗ: x |
|
R. |
|
9 |
3 |
|
x2+4x |
|
27 |
|
x |
|
|
|
|
||||||||||||
|
Решите неравенство |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем обе части неравенства к одинаковому основанию 1 |
|||||||||||||||||||||||||||
|
3 |
|
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
|
3 |
3. |
||||||||||
|
|
|
|
; |
|
|
: |
|||||||||||||||||||||
|
|
1 |
|
2 |
1 |
x2+4x |
|
1 |
|
|
3 |
|
1 |
|
|
x2+4x 2 |
1 |
3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как основание показательной функции 0 < 1=3 < 1, то показательная функция монотонно
убывающая. При переходе к неравенству в показателе степени знак неравенства меняется на противоположный:
x2 4x+2 3, x2 4x 5 0. Решим неравенство методом интервалов.
-1 |
5 |
x |
|
x 2 (1; 1] [ [5; +1). Ответ: (1; 1] [ [5; +1)
4. Вычислите cos2 3 + cos2 cos 4 cos 2
Решение. Применим формулу понижения степени и формулу преобразования произведения тригонометрических функций в сумму:
cos2 3 + cos2 cos 4 cos 2 =
= |
1+cos |
6 |
+ |
1+cos 2 |
|
1 |
(cos 6 + cos 2 ) = |
2 |
|
2 |
2 |
||||
= 1+cos |
6 +1+cos 2 cos 6 cos 2 = 1: |
||||||
|
|
|
|
2 |
|
|
|
Ответ: 1
13
5. Решите уравнение (x 3) p2x 3 + px 1 = 2 (x 3)
Решение. Перенесем все слагаемые в одну сторону и вынесем общий множитель (x 3)
(x 3) p2x 3 + px 1 2 = 0:
Это уравнение равносильно совокупности
"
x 3 = 0;
p2x 3 + px 1 2 = 0:
Решим каждое уравнение. Затем обязательно выполним проверку, чтобы отбросить посторонниå êîðíè.
x 3 = 0 ) x1 = 3. Решим уравнение p2x 3+px 1 2 = 0.
Уединим один из радикалов, затем возведем обе части в |
||||||||||||||||
êâадрат, чтобы избавиòüñÿ îò âíåøнего корня. |
|
|
|
|
||||||||||||
2x 3 = 4 4 x 1 + x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
p2x 3 = 2 px 1, |
p2x 3 |
2 = 2 px 1 |
2, |
|||||||||||||
|
p |
|
|
|
, |
4px |
|
1 = 6 |
|
x. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Замечание. Решение уравнения с одним квадратным корнем |
||||
сводится к решению системы |
( f(x) = '2(x): |
|||
p |
|
|
, |
|
|
f(x) = '(x) |
|
'(x) 0; |
|
Так как значение квадратного корня всегда положительное число, то отсюда следует ограничение на значение
переменной x: x 6. Этим ограничением можно воспользоваться при отборе корней уравнения.
Повторно возведем обе части уравнения в квадрат, чтобы |
|
избавиться от внешнего корня: 4px 1 2 |
= (6 x)2, |
14
16x 16 = 36 12x + x2, |
x2 28x + 52 = 0, |
x2 = 2 |
|||||||
èëè |
x3 = 26 (x3 = 26 постороннее решение, так как не |
||||||||
удовлетворяет ограничению |
x 6). |
|
|
||||||
Проверка. |
0 (p |
|
+ p |
|
|
|
|
|
|
|
|
|
|
|
= 2 0, |
0 = 0 истина, |
|||
x1 |
= 3 |
3 |
2) |
||||||
)x1 = 3 является корнем уравнения. Замечание. Здесь
один из множителей обращается в ноль. При проверке нужно обязательно показать, что второй множитель, содержащий иррационалüности, не теряет смысла.
x2 = 2 1 (p1 + p1) = 2 ( 1),
) x2 = 2 является корнем уравнения.
x3 = 26 23 (p49+p25) = 2 23 ) 23 12 = 23 2 ложно,
) x3 = 26 2 ? (Это так же следует из вышеприведенного ограничения на значения переменной x: x 6.)
Ответ: 2; 3
6. Решите неравенство (log3 3x)2 3 log3 x > 7 Решение. ОДЗ: x > 0, òî åñòü x 2 (0; +1).
Воспользуемся свойством логарифма.
(log3 3 + log3 x)2 3 log3 x 7 > 0,
(1 + log3 x)2 3 log3 x 7 > 0, (log3 x)2 log3 x 6 > 0.
Введем новую переменную: log3 x = t, t 2 R. Неравенство
примет вид |
t2 t 6 > 0. |
Найдем нули функции |
|
f(t) = t2 t 6. |
t1 = 2, t2 |
= 3. Изобразим решение |
|
неравенства |
t2 t 6 > 0. |
|
|
15

-2 3 |
|
t |
" t > 3: Вернемся к прежней переменной. |
||
t < 2; |
|
|
log3 x < 2; |
|
log3 x < log3 3 2; |
" log3 x > 3: |
) |
" log3 x > log3 33: |
Так как основание логарифма 3 > 1, то логарифмическая функция монотонно возрастающая. При переходе к неравенству для выражений" под знаком логарифма знак
x < 1;
неравенства сохраняется. 9
x > 27:
Учитывая ОДЗ, получим x 2 (0; 1=9) [ (27; +1)
0 |
1 |
27 |
x |
|||
|
|
|
|
|||
|
9 |
|
|
|
|
|
Ответ: |
|
|
|
|
||
(0; 1=9) [ (27; +1) |
|
|||||
7. Дано уравнение |
|
1 |
1 = ctgx cos x. |
|||
|
|
|
sin x |
|||
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
[0; 4 ].
Решение. а) ОДЗ: sin x =6 0 ) x =6 n, n 2 Z. Найдем
общее решение уравнения. Воспользуемся определением |
|||||||||||||||||||||
ctgx = cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
1 = |
cos x |
cos x, |
|
1 |
1 = cos x |
1 |
1 . |
||||||||||||
sin x |
sin x |
|
sin x |
sin x |
|||||||||||||||||
|
1 |
|
1 cos x |
|
1 |
|
1 |
= 0, |
|
1 |
1 |
|
(1 |
|
cos x) = 0. |
||||||
sin x |
sin x |
|
|
|
|
|
|
|
|||||||||||||
|
|
sin x |
|
|
|
|
|||||||||||||||
16
, |
" |
1 |
|
|
cos x = 0: |
) |
" cos x = 1: |
) |
||
|
|
|
1 |
|
1 = 0; |
|
sin x = 1; |
|
||
|
|
|
sin x |
|
|
|||||
x = + 2 n; |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
Z |
|
|
|
|||
" x = 2 k; k |
|
|
Z:2 |
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученное решение x = 2 k; k 2 Z, не удовлетворяет ОДЗ.
б) Найдем углы, удовлетворяющие условию
Подставим в общее решение x = 2 + 2 n,
значения n. Так как задан отрезок положительных значений углов, то и значения n будем брать целые положительные.
n = 0 ) x = 2 |
2 [0; 4 ], |
n = 1 |
|
) x = |
5 |
2 [0; 4 ]. |
||
|
2 |
|||||||
Для остальных |
n x 2= [0; 4 ]. |
|
|
|
|
|
||
Ответ: |
à) |
|
á) |
; |
5 |
|
||
|
2 + 2 n; n 2 Z; |
2 |
2 |
|
|
|
||
Замечание. Как общее решение, так и отобранные углы могут быть записаны только в градусах. Например, найдем углы, удовлетворяющие условию 0 x 720 . Для этого
будем подставлять в общее решение x = 90 + 360 n целые значения n. Так как задан отрезок положительных значений углов, то и значения n будем брать целые положительные.
n = 0 ) x = 90 2 [0 ; 720 ], n = 1 ) x = 450 2 [0 ; 720 ].
Для остальных n x 2= [0 ; 720 ]. В решении пункта б) необходимо выполнить полный перебор значений n и показать, что при других значениях n найденные корни
уравнения не войдут в заданный отрезок значений углов. Неполный перебор считается ошибкой, и экзаменатор
17
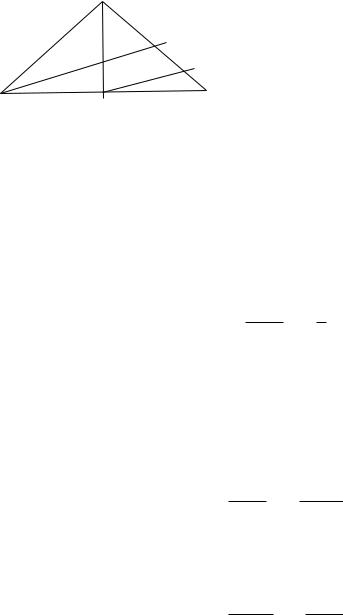
имеет право снизить установленные за задачу баллы.
Ответ: |
|
90 + 360 n; 90 ; |
450 |
|
Ïðè ýòîì |
смешанная |
запись |
единиц измерения |
углов, |
такая как, |
например, |
||
x = 90 + 2 n считается грубой ошибкой. |
|
|||||
8.В треугольнике ABC медиана AM в отношении 5:3, считая от вершины длин сторон треугольника AC è BC
делит биссектрису CK C. Найдите отношение (большей к меньшей).
|
C |
|
|
|
|
|
|
|
M |
|
|
|
|
|
O |
N |
|
|
|
|
|
|
|
|
|
|
|
A |
K |
B |
|
|
|
|
|
|
|
|
|
|
|
Äàíî: CM = MB = |
1BC, |
CK биссектриса, CO |
= |
5 |
||
AC |
|
|
2 |
OK |
|
3 |
=? |
|
|
|
|
|
|
BC |
|
|
|
|
|
|
Решение. Пусть O точка пересечения медианы AM и биссектрисы CK. Дано отношение
OKCO = 53:
Проведем прямую KN параллельно медиане AM
(Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.) ) рассматривая \KCB,
OKCO = MCMN :
Те же прямые пересекают стороны угла \ABC:
MB = AB :
MN AK
18

Òàê êàê M середина стороны BC ) CM = MB )
CO |
= |
CM |
= |
MB |
= |
|
AB |
; |
5 |
= |
|
AB |
) KB = 2 части: |
|
|
|
|
|
|
|
|
|
|
||||||
OK |
MN |
MN |
AK |
3 |
AK |
|||||||||
Òàê êàê CK биссектриса, то по свойству биссектрисы
Èòàê, AC
CB
AK |
= |
AC |
) |
|
AC |
= |
3 |
= 1;5: |
|
|
|
|
|
||||
KB |
CB |
CB |
2 |
|||||
= 1;5.
Ответ: CBAC = 1;5
Замечание. Решение геометрических задач часто вызывает трудности у абитуриентов. Ведь геометрические задачи настолько многообразны, что невозможно дать какиелибо общие указания к их решению. Редко какая задача в геометрии может быть решена только с использованием определенной формулы. При решении большинства задач необходимо свободно владеть всем теоретическим материалом.
Выполняя чертеж (рисунок), стремитесь сделать его соответствующим условиям задачи. Так, если сказано, что некоторый угол вдвое больше другого или отрезки перпендикулярны, отразите это на чертеже. Хороший чертеж это удобный для восприятия наглядный способ записи условий задачи, он может стать помощником в решении задачи, подсказать правильный ход рассуждений. В то же время, правильный чертеж ничего не доказывает, так как все должно быть обосновано соответствующим логическим выводом.
Начиная решать задачу, используйте определения и свойства входящих в задачу данных и искомых элементов,
19
ведите рассуждения: треугольник равнобедренный, следовательно, : : :, две касательные проведены из
одной точки, следовательно, : : :, окружность описана около прямоугольного треугольника, следовательно, : : :.
Вспомните теоремы, в которых связаны данные и искомые элементы задачи, вспомните похожие задачи.
9. Найдите все значения параметра a, при которых система
уравнений (
log2 x + log2 y = 6; y = 8 + a(x 6)
имеет два различных решения.
Решение. ОДЗ: x > 0, y > 0, a 2 R. Используя свойства
логарифма, исходная(система примет вид
xy = 64;
y = 8 + a(x 6):
Подставив y в первое уравнение системы, получим
ax2 (6a 8)x 64 = 0:
Система уравнений будет иметь два различных решения, если квадратное уравнение будет иметь два различных корня, принадлежащих ОДЗ.
Âпервую очередь нужно рассмотреть случай, когда a = 0.
Âэтом случае полученное уравнение имеет единственный корень x = 8, что не подходит по условию задачи.
Следовательно, a =6 0.
Для случая два различных положительных корня имеем
20
