
8693
.pdf
Решение задач варианта 3.
1.Решите неравенство j2x 12j + jx + 9j > 18
Решение. ОДЗ: x 2 R.
Приравняем к нулю выражения под знаком модуля
2x 12 = 0, x+9 = 0 ) x = 6, x = 9. Нанесем эти точки
на числовую прямую и рассмотрим решение неравенства на каждом из трех промежутков, раскрывая знаки модулей.
I II III
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
-9 |
|
|
6 |
x |
|
|
|
( |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
I. |
|
(2x |
12) |
|
|
(x + 9) > 18; |
) |
3x > 15; |
) |
||||||||
|
|
|
x < |
|
|
9; |
|
|
|
|
|
|
x < 9; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
x < |
|
|
9; |
|
|
|
|
|
|
|
|
||||
|
|
( x < |
5: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II. |
Решение системы неравенств: x 2 (1; 9). |
|
||||||||||||||||
( |
(2x 12) + x + 9 > 18; |
) ( x < 3: |
|
|
||||||||||||||
|
|
|
9 x < 6; |
|
|
9 x < 6; |
|
|||||||||||
|
|
Решение системы неравенств: x 2 [ 9; 3). |
|
|
||||||||||||||
III. |
( |
x |
|
|
6; |
|
|
|
|
|
|
( |
x 6; |
|
x 6; |
|
||
2x |
|
12 + x + 9 > 18; ) |
3x > 21; |
) ( x > 7: |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение системы неравенств: x 2 (7; +1).
Решением исходного неравенства является объединение всех трех решений
x 2 (1; 9) [ [ 9; 3) [ (7; +1) ) x 2 (1; 3) [ (7; +1)
Ответ: (1; 3) [ (7; +1) .
31

2. Через точку M(x; y) графика функции
f(x) = ln(x 2) 0; 5x2 проведена касательная. Угловой коэффициент этой касательной равен 2. Найдите координаты точки M.
Решение. |
ÎÄÇ: x > 2. Òàê |
как геометрический смысл |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||
производной функции в данной точке x0 |
f0(x0) = k |
, |
||||||||||||||||
ãäå k |
угловой |
коэффициент |
касательной, |
òî |
получаем |
|||||||||||||
f0(x) = (ln(x |
|
2) |
|
0; 5x2)0 |
= |
1 |
|
|
x. Тогда |
1 |
|
|
x = 2, |
|||||
x 2 |
x 2 |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
||||||||||
(x 2) |
= 0, |
|
) (x 2)2 = 1, |
|
|
|
|
|
||||||||||
x 2 |
|
|
|
|
|
|
||||||||||||
) x1 = 1 |
èëè |
|
x2 = 3. |
x1 2 ?, òàê êàê x > 2, |
|
x2 = 3 |
||||||||||||
удовлетворяет ОДЗ.
Найдем координаты точки M. f(3) = ln 1 0; 5 32 = 4; 5. Тогда координаты точки M(3; 4; 5).
Ответ: M(3; 4; 5)
|
|
|
|
|
102+21 |
|
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. Вычислите |
|
|
|
|
lg 75 2 lg(2 p3). |
|
|
|
|
|
|
= |
|||||||
Решение. 102+2 |
lg 75 2 lg(2 p3) = 100 10 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
1 |
|
4 |
|
|
|
|
lg p75 |
lg |
2 3 |
4 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
75 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= 100 10lg |
4 p3 |
|
= 100 41 q753 = 25 5 = 125. |
|
|
|
|||||||||||||
Ответ: 125
pp
4.Решите уравнение 3 x 81 10 x 9 + 3 = 0.
Решение. ОДЗ: x 2 N, x > 1.
2 1
Перепишем уравнение в виде 3 9 x 9 9 x + 3 = 0.
1
Пусть 9 x = t, t > 0. Получаем квадратное уравнение относительно t:
3t2 10t + 3 = 0, откуда
32

" t2 = 31 |
) |
" 9 x = |
31 ) " |
t1 = 3; |
|
1 |
|
|
9 x = 3; |
||
|
|
1 |
|
"
)x = 2; x = 2
Íî x2 = 2 не удовлетворяет ОДЗ
3x |
= 3 1 |
) " x2 = 1 |
|
2 |
|
2 |
= 1; |
3 x = 31; |
|||
|
|
x |
|
2 |
|
|
) x = 2.
Ответ: 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Решите уравнение |
|
lg(x + 1)2 + lg(x + 9)2 = 2 lg 9. |
|
||||||||||||||
Решение. |
ÎÄÇ: |
( |
(x + 1)2 > 0; |
) x 6= 9, |
x 6= 1. |
|
|||||||||||
(x + 9)2 > 0 |
|
||||||||||||||||
Используя свойства логарифма, получим |
|
|
|||||||||||||||
2 lg jx + 1j + 2 lg jx + 9j |
= |
2 lg 9, |
откуда |
находим, |
÷òî |
||||||||||||
lg j(x + 1)(x + 9)j |
= |
lg 9 |
è |
далее |
jx2 + 10x + 9j = |
9. |
|||||||||||
Последнее |
равенство |
выполняется |
â |
любом из следующих |
|||||||||||||
|
|
|
|
x2 + 10x + 9 = 9; |
9; |
) |
|
x2 + 10x = 0; |
) |
||||||||
случаев: " x2 + 10x + 9 = |
" x2 + 10x + 18 = 0; |
||||||||||||||||
|
x1 |
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 x2 |
= 10; |
|
|
|
|
|
|
|
|
|
|||||||
6 x3 |
= 5 + p |
|
|
; |
|
|
|
|
|
|
|
|
|
||||
7 |
|
|
|
|
|
|
|
|
|
||||||||
6 x |
|
|
p |
|
: |
|
|
|
|
|
|
|
|
|
|||
4 |
= 5 |
7 |
|
|
|
|
|
|
|
|
|
||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, уравнение имеет четыре корня, удовлетворяющих ОÄÇ.
Ответ: 10; 5 p7; 5 + p7; 0
6.Решите уравнение (x2 9) p 3x 5 + p 2x = 3x2 27
Решение. Перенесем все слагаемые в одну сторону и вынесем общий множитель за скобку.
33

(xx2 9 |
= 0; |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||
2 |
9) |
|
p |
3x |
|
|
|
5 |
+ p |
|
2x |
|
3 = 0 |
|
|
|
|
||||||||
" p |
|
3x |
|
5 + p |
|
|
2x |
|
|
3 = 0 ) |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x + 3 = 0; |
|
|
|
|
|
|
|
|
|
|
|
x1 = 3; |
|||||||||||||
6 p 3x 5 + p 2x = 3 |
) |
6 p 3x 5 + p 2x = 3 |
|||||||||||||||||||||||
2 x 3 = 0; |
|
|
|
|
|
|
|
|
|
2 x2 |
= 3; |
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
Решим иррациональное |
уравнение и |
затем обязательно |
|||||||||||||||||||||||||
ñäелаем пðîâåðêó для всех найденных корней. |
|
||||||||||||||||||||||||||
p 3x 5 + p 2x = 3. Уединим один из радикалов |
|
||||||||||||||||||||||||||
p |
|
= 3 p |
|
|
|
|
|
и возведем обе части в квадрат |
|||||||||||||||||||
3x 5 |
2x |
||||||||||||||||||||||||||
3x 5 = 9 6p |
|
|
|
2x, 6p |
|
|
= x + 14. |
|
|||||||||||||||||||
2x |
2x |
|
|||||||||||||||||||||||||
Возведем еще раз обе части в квадрат |
|
|
|
||||||||||||||||||||||||
72x = x2 + 28x + 196, |
|
|
x2 + 100x + 196 = 0 ) x3 = 98, |
||||||||||||||||||||||||
x4 = 2. Выполним проверку. |
|
|
|||||||||||||||||||||||||
|
0 (p |
|
|
|
|
+ p |
|
|
|
|
|
|
|
0 = 0 истина, ) |
|||||||||||||
x1 = 3 |
9 5 |
6) = 3 0, |
|||||||||||||||||||||||||
x1 = 3 является корнем уравнения. |
|
|
|||||||||||||||||||||||||
|
0 (p |
|
+ p |
|
|
|
|
|
|
|
|
||||||||||||||||
x2 = 3 |
14 |
6) = 3 0, не имеет смысла, ) |
|||||||||||||||||||||||||
x2 = 3 не является корнем уравнения. |
|
|
|||||||||||||||||||||||||
x3 = 98 |
( 98)2 9 |
|
|
(p |
|
|
+ p |
|
= 3 ( 98)2 9 , |
||||||||||||||||||
|
|
289 |
196) |
||||||||||||||||||||||||
17 + 14 = 3 |
ложно, |
|
) x3 = 98 |
не является корнем |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x4 = 2 (4 9) (p |
|
+ p |
|
|
|
||||||||||||||||||||||
1 |
4) = 3 (4 9), 1 + 2 = 3, |
3 = 3 |
|||||||||||||||||||||||||
истина, ) x4 = 2 является корнем уравнения. Ответ: 2; 3
34

7. Дано уравнение
p
2 sin 4x sin x sin 7x = 0:
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
[2 ; ].
Решение. |
|
а) Сгруппируем последние слагаемые и применим |
|||||||||||||||||||||||||||
формулу |
|
|
преобразования |
суммы |
|
|
|
|
тригонометрических |
||||||||||||||||||||
ôóнкций в произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
p2 sin 4x (sin x+sin 7x) = 0, |
p |
|
sin 4x 2 sin 4x cos 3x = 0. |
||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||
Вынесем общий множитель sin 4x (p |
|
|
2 cos 3x) = 0 |
||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||
sin 4x = 0; |
|
|
|
|
|
|
|
sin 4x = 0; |
|
|
|
|
|||||||||||||||||
, " p |
|
|
|
|
|
|
|
, |
|
" cos 3x = |
|
p |
|
; |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||
2 |
2 |
cos 3x = 0; |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
) |
|
|
|
|
4x = n; n 2 Z; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|||||||||
|
|
|
|
3x = |
|
arccos( |
p |
2 |
) + 2 k; k |
2 |
|
Z; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4x = n; n 2 Z; |
|
|
|
|
|
|
|
x = n4 ; n 2 Z; |
|
|
|||||||||||||||||||
" 3x = |
|
|
|
|
+ 2 k; k |
|
|
Z; |
) |
|
" x = |
|
|
|
|
+ 2k ; k |
|
Z: |
|||||||||||
|
2 |
|
12 |
2 |
|||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||
б) Найдем углы, удовлетворяющие условию [2 ; ].
n = 0 |
) x = 0 2= [2 ; ], |
n = 1 |
) x = 4 2= [2 ; ], |
n = 2 |
) x = 2 2 [2 ; ], |
||
n = 3 |
) x = |
3 |
2 [2 ; ], |
4 |
|||
n = 4 |
) x = 2 [2 ; ]. |
||
k = 0 ) x = 12 2= [2 ; ],
35
k = 1 ) x = |
7 |
2 [2 ; ], x = |
3 |
2 [2 ; ], |
|
|
|
|
|||||||
12 |
4 |
|
|
|
|
||||||||||
Убеждаемся, что для всех остальных n è k |
x 2= [2 ; ]. |
|
|||||||||||||
Ответ: |
à) n |
|
|
2k |
|
|
; á) |
|
, 7 |
3 |
|||||
|
4 ; n 2 Z; |
|
|
+ |
|
; k 2 Z |
|
2 , |
|
12 , |
|
||||
|
12 |
3 |
|
4 |
|||||||||||
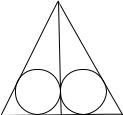
8.В правильном 4ABC, сторона которого равна a, проведена высота BK. Â 4ABK è 4BCK вписано по окружности и
к ним проведена общая касательная, отличная от стороны AC. Найдите площадь треугольника, отсекаемого этой
касательной от 4ABC.
Решение.
B
D M E
A K C
Решение. Воспользуемся извесòными формулами: |
|||||
|
a2p3 |
|
S |
|
|
S4ABC = |
|
; |
r = |
|
: |
4 |
p |
||||
Òàê êàê 4DBE тоже правильный ( \BDE = \BAC = 600
è \DEB = \ACB = 600 как углы при параллельных прямых |
||||||||||
AC è DE и секущих AB, BC), то его площадь может быть |
||||||||||
найдена по формуле |
|
|
(DE)2p |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
S4DBE = |
3 |
: |
|
|
||||||
|
|
4 |
|
|
|
|
|
|||
|
p |
|
|
|
|
|
|
|
|
|
Высота BK = AB sin A = |
a |
3 |
. Найдем BM. |
|||||||
2 |
|
|||||||||
|
|
|
|
|
ap |
|
|
|
||
BM = BK MK = |
3 |
2r: |
||||||||
2 |
|
|
|
|||||||
36

Радиус вписанной в 4ABK окружности равен
|
|
|
|
a2p |
|
|
|
|
|
|
|
|
|
|
|
||
|
S4ABK |
|
|
3 |
|
|
|
|
|
a |
|
||||||
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
||||
r = |
|
= |
|
|
|
|
|
|
ap |
|
|
= |
|
2(1 + p |
|
|
: |
p |
|
|
|
|
|
|
|
|
|||||||||
1 |
(a + |
a |
+ |
3 |
) |
|
3) |
||||||||||
|
|
2 |
|
|
|
||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|||||||
Отсюда |
ap |
|
|
|
|
|
|
|
|
|
|
3 |
|
a |
|
a |
|
||||||
BM = |
|
|
|
|
2(1 + p |
|
|
= |
|
|
: |
2 |
|
|
2 |
||||||||
|
|
3) |
|||||||||
Òàê êàê 4ABC 4DBE (по двум сторонам и углу между ними), то
BM
BK
Тогда
Ответ:
= DEAC
S4DBE
a2p3 12
|
|
|
|
|
|
|
|
|
|
|
|
BM |
|
|
a |
2 |
|
|
|
|
a |
|
||||
) DE = AC |
|
= a |
|
|
|
ap |
|
|
= p |
|
: |
|||||||||||||||
BK |
2 |
|
||||||||||||||||||||||||
|
3 |
3 |
||||||||||||||||||||||||
|
|
a |
2p |
|
|
|
2p |
|
|
|
|
|
|
|
|
|
|
|
|
2p |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(p |
|
) |
3 |
|
a |
3 |
|
|
|
|
|
|
|
|
|
|
a |
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= |
|
3 |
|
= |
|
. |
Èòàê, |
S4DBE = |
|
. |
|
|
||||||||||||||
4 |
|
|
12 |
|
|
12 |
|
|
|
|||||||||||||||||
9. Найдите |
все значения параметра a, при каждом из |
|
которых |
существует |
хотя бы одно решение системы |
x2 + (5a + 2)x + 4a2 + 2a < 0; |
||
( x2 + a2 = 4: |
|
|
Решение. |
ÎÄÇ: x 2 R, |
a 2 R. |
Применим координатно-параметрический метод: на плоскости aOx найдем множество точек (a; x), значение
параметра и координаты каждой из которых удовлетворяют смешанной системе. Рассмотрим первое неравенство системы.
x2 + (5a + 2)x + 4a2 + 2a < 0 , (x + 4a + 2) (x + a) < 0.
Применяем метод частичных областей: определяем знак выражения F (a; x) = (x + 4a + 2) (x + a) между прямыми
x = a è x = 4a 2. На координатно-параметрической
37

плоскости множество всех точек (a; x), значение параметра и
координаты каждой из которых удовлетворяют неравенству (x + 4a + 2) (x + a) < 0 заштриховано.
x=-a |
|
2 |
|
x2 + a2=4 |
|
|
|
|
- |
16 |
2 |
|
17 |
|
|
|
-2 |
- 2 |
0 |
2 |
|
|||
|
|
-2 |
x=-a |
|
|
|
|
|
x=-4a-2 |
|
|
a
Второе уравнение системы x2 + a2 = 4 представляет собой
на координатно-параметрической плоскости окружность с центром в начале координат, радиусом R = 2. Найдем точки
пересечения прямых x = a è x = 4a 2 с окружностью
x2 + a2 = 4.
(
x = a;
x2 + a2 = 4;
(
x = 4a 2; x2 + a2 = 4;
"x = p2; a = p2;
,x = p2; a = p2;
"
x = 2; a = 0;
,x = 3017; a = 1617:
Искомое множество решений смешанной системы представляет собой дуги окружности x2+a2 = 4, находящиеся
внутри заштрихованíой области. |
|
|
||||||||
Таким образом, p2 < a < 1716 |
; 0 < a < p |
|
. |
|||||||
2 |
||||||||||
Ответ: |
|
p |
2; 1716 [ 0; p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|||||
38

Таблица ответов для Варианта 3
|
1 |
|
|
|
|
|
|
2 |
|
|
3 |
4 |
|
|
|
|
||||||
(1; 3) [ (7; +1) |
|
|
M(3; 4; 5) |
|
125 |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p5 |
|
|
|
|
|
p |
|
|
6 |
|
|
|
|
;77 3 |
a28p |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||
|
|
|
|
|
|
2; 3 |
|
|
||||||||||||||
10; 5 7; 5 + |
7; 0 |
|
2 ; |
12 ; 4 |
12 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
169 |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( |
2; 17) [ (0; |
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3. Варианты заданий для самостоятельного решения Вариант 1
1. Упростите до числового ответа |
|
|
a3 |
|
! |
|
|
||||||
|
a3 |
+ 2(ab)3 |
+ 4b3 |
|
|
|
|
|
|||||
|
|
a |
1 |
(a 8b) |
|
a |
1 |
2b |
1 |
|
1 |
a3 |
|
|
|
|
3 |
|
|
|
|
3 |
|
3 |
|
|
2 |
|
2 |
|
|
1 |
2 |
|
|
|
1 |
|
|
|
|
2.Два подъ¼мных крана, работая вместе, разгрузили баржу за
6 часов. За какое время может разгрузить баржу каждый кран, работая отдельно, если один из них может е¼ разгрузить на 5 часов скорее, чем другой?
3.Решите неравенство 22x 15 11x < 11x 15 122x+3. Â ответе укажите наименьшее целое решение.
4. Вычислите |
5 sin 2 |
3 |
, åñëè tg = 2 |
cos 2 |
5. Решите уравнение
x2 36 p 5 6x p1 3x = 3x2 108
39
6. |
Решите неравенство |
log2(x + 15) 2 log4(15 x) 2. Â |
||||
|
ответе укажите наименьшее целое решение. |
|
||||
7. |
Дано уравнение |
|
|
|
|
= 0: |
|
2 cos 2x + 2p2 cos x + 2 |
|||||
|
|
|
|
|
|
|
а) Решите уравнение.
б) Найдите корни этого уравнения, принадлежащие отрезку
[ =2; 2 ].
8.Периметр равнобедренного треугольника относится к его боковой стороне как 18:5. Найдите отношение радиусов вписанной и описанной окружностей.
9. При каких |
значениях |
параметра |
a |
уравнение |
|||
|
|
|
p |
|
|
|
|
x2 (4a 5)x + 3a2 |
15a |
x + 15 |
= |
0 |
имеет ровно |
||
два решения? |
|
|
|
|
|
|
|
|
|
q |
|
|
Вариант 2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Вычислите |
16 |
1 |
+ 64 |
1 |
+ 248 |
||||||||||||
log 5 2 |
log 3 4 |
|||||||||||||||||
2. |
Решите уравнение |
|
|
|
|
jx + 1j + j3x 9j = 8 |
||||||||||||
4. |
Вычислите |
|
|
2 |
|
|
|
|
9 |
2 |
|
|
|
|
|
|
|
|
3. |
Решите неравенство |
|
|
|
|
2 |
x2+x |
|
(20; 25)2x 7 |
|||||||||
|
|
cos |
|
3 + cos cos 4 cos 2 |
||||||||||||||
5. |
Решите уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x + 1) p |
|
+ p |
|
= 6 (x + 1) |
|||||||||||||
|
3x + 1 |
19 3x |
||||||||||||||||
6. |
Решите неравенство |
|
|
|
|
|
|
|
x |
|
|
x |
||||||
|
|
|
|
|
|
|
|
log2 2 2 log2 2 1 |
||||||||||
40
