Глава 2
2 КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
2.1 Кинематика точки 2.1.1 Основные понятия
Кинематика – раздел механики, изучающий геометрические свойства движения тел без учета их инертности и действующих на них сил.
Кинематические зависимости в теоретической механике формулируются в привычном для нас обычном (евклидовом) пространстве и с использованием понятия абсолютного времени t.
Все кинематические величины – функции времени t; момент времени t = 0 в большинстве задач означает начало отсчета, некоторый условный момент времени.
Кинематически задать движение тела – значит, задать его положение относительно данной системы отсчета в любой момент времени.
Основная задача кинематики – зная закон движения тела (точки), установить все остальные кинематические величины, характеризующие движение.
Наиболее употребительными в кинематике являются такие величины:
1)траектория;
2)скорость точки (тела);
3)ускорение точки (тела).
Эти величины фигурируют во всех задачах кинематики, часть их может входить в условия задачи, остальные подлежат определению.
На первом этапе обсуждаем кинематику точки.
Траекторией называется непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета.
Если траектория – прямая линия, движение называется
прямолинейным, иначе – криволинейным.
Движение точки может быть задано тремя способами:
•векторным способом;
•координатным;
•естественным.
44
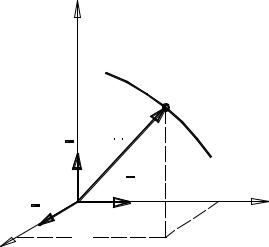
1.Векторный способ
Влюбой момент времени t положение точки можно определить
радиус-вектором r (рисунок 2.1); описание движения сводится к построению зависимости
|
r = r(t). |
|
(2.1) |
|
|
Z |
|
|
|
|
|
|
M |
|
|
k |
r |
z |
|
|
|
|
||
|
|
j |
|
|
i |
O |
|
Y |
|
|
x |
|||
|
|
|||
X |
y |
|
|
|
Рисунок 2.1 – К векторному описанию движения
Геометрическое место концов вектора r (годограф вектора) определяет траекторию движения.
Если rx = x, ry = y, rz = z, то |
|
r = xi + yj +zk. |
(2.2) |
2. Координатный способ |
|
Если задать |
|
x = f1(t), y = f2(t), z = f3(t) , |
(2.3) |
то соотношения (2.3) представляют собой уравнения движения точки в прямоугольных декартовых координатах.
Аналогичные зависимости можно записать для цилиндрических, сферических и т.д. систем координат.
В случае, когда точка движется в плоскости, задают
x = f1(t), y = f2(t), |
(2.4) |
а при движении вдоль прямой, принимая ее за ось Х,
x = f(t). |
(2.5) |
По существу, (2.3) и (2.4) представляют собой т.н. параметрическое задание траектории. Исключая t, получаем привычные формы записи y = y(x) и т.д.
45
Можно заключить, что векторный способ и координатный практически переходят друг в друга, и в известном смысле они идентичны. Однако координатный способ связан с выбором системы координат. Даже если мы рассмотрим две декартовы системы, сдвинутые и повернутые относительно друг друга, получим разные записи законов движения в координатной форме. Тем более разница скажется, если мы рассмотрим переход, например, от декартовых координат к цилиндрическим, сферическим и т. д.
3. Естественный (траекторный) способ
|
Z |
A |
|
|
O |
|
s M |
|
B |
0 |
Y |
|
X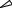 
Рисунок 2.2 – К траекторному описанию движения
Этот способ описания движения удобен, когда траектория точки известна. В этом случае, принимая на траектории некоторую точку О за начало отсчета и определив положительное направление этого отсчета, закон движения можно представить в виде (рисунок 2.2)
s = s (t), |
(2.6) |
где s – расстояние от начала отсчета, измеренное вдоль траектории, называемое дуговой координатой.
Таким образом, при этом способе нужно задать:
1) траекторию; 2) начало отсчета; 3) положительное направление отсчета дуговой координаты; 4)закон движения в виде (2.6).
Следует отметить, что s – не путь, пройденный точкой, а ее текущее положение. Например, при колебаниях величина s меняется в некоторых конечных пределах, а пройденный точкой путь все время растет.
2.1.2 Вектор скорости точки
Перемещение точки за время ∆t определится вектором ∆r = =r1 – r = MM1 (r1 – текущий радиус-вектор точки М1, r – исходный для точки М,
рисунок 2.3). Если траектория прямолинейна, то приращение ∆r – вдоль этой траектории, если криволинейна – то по хорде.
46
Z |
|
|
vcp |
v |
|
M1 |
|
|
|
|
|
r1 |
r |
M |
|
||
|
r |
Y |
0 |
|
|
|
|
X 
Рисунок 2.3 – К определению вектора скорости
Средняя скорость определяется как отношение смещения за некоторое время к величине этого времени:
vср = ∆r / ∆t. |
(2.7) |
Скорость в данный момент времени (мгновенная скорость) определяется предельным переходом при уменьшении интервала времени:
vср = lim(vcp) = lim |
∆r |
= dr . |
(2.8) |
|
∆t→0 |
∆t→0 |
∆t |
dt |
|
Направление вектора скорости – по касательной к траектории в сторону движения. Можно заметить, что средняя и мгновенная скорости по величине совпадают, если в рассматриваемом интервале времени скорость движения постоянна, а по направлению совпадение этих скоростей будет только при прямолинейном движении.
Размерность скорости соответственно получается как отношение единицы длины (пройденного пути) к единице времени:
[v] = м/с, см/мин, км/час и т.д.
2.1.3 Вектор ускорения точки
Ускорением точки называется векторная величина, характеризующая изменение скорости (по модулю и направлению) с течением времени.
За время ∆t скорость меняется на величину ∆v = v1 – v. Вектор
приращения скорости ∆v всегда направлен в сторону вогнутости траектории. Это легко можно установить, рассмотрев два смежных направления вектора скорости точки при ее движении по криволинейной траектории. Среднее ускорение (рисунок 2.4) определяется формулой
47