
- •Министерство науки и высшего образования Российской Федерации
- •ВВЕДЕНИЕ
- •1. МЕХАНИКА И ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
- •1.2 Сложение сил. Система сходящихся сил
- •1.3 Момент силы относительно центра. Пара сил
- •1.4 Приведение системы сил к центру. Условия равновесия
- •1.5 Плоская система сил
- •1.6 Трение
- •1.7 Пространственная система сил
- •1.8 Центр тяжести
- •2 КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
- •2.1.2 Вектор скорости точки
- •2.1.3 Вектор ускорения точки
- •2.1.4 Определение скорости и ускорения при координатном задании движения
- •2.1.5 Примеры решения задач кинематики точки
- •2.1.6 Оси естественного трехгранника. Числовые значения скорости. Касательное и нормальное ускорение точки
- •2.1.7 Частные случаи движения точки
- •2.1.8 Графики движения, скорости и ускорения точки
- •2.1.9 Примеры решения задач
- •2.1.10 Скорость и ускорение точки в полярных координатах
- •2.2 Поступательное и вращательное движения твердого тела
- •2.2.1 Поступательное движение
- •2.2.2 Вращательное движение твердого тела вокруг оси. Угловая скорость и угловое ускорение
- •2.2.3 Равномерное и равнопеременное вращения
- •2.2.4 Скорости и ускорения точек вращающегося тела
- •2.3 Плоскопараллельное движение твердого тела
- •2.3.1 Уравнения плоскопараллельного движения. Разложение движения на поступательное и вращательное
- •2.3.2 Определение траекторий точек плоской фигуры
- •Рисунок 2.15 – К определению траекторий точек тела
- •Рисунок 2.16 – Схема эллипсографа
- •2.3.3 Скорости точек плоской фигуры
- •Рисунок 2.17 – Определение скорости точки на ободе колеса
- •2.3.4 Теорема о проекциях скоростей двух точек тела
- •Теорема
- •2.3.5 Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Центроиды
- •2.3.6 Ускорения точек плоской фигуры
- •Пример 1.
- •Рисунок 2.23 – К определению ускорений точек колеса
- •Пример 2.
- •Рисунок 2.24 – Задача о шестеренках
- •2.4 Движение твердого тела вокруг неподвижной точки и движение свободного твердого тела
- •2.4.2 Общий случай движения свободного твердого тела
- •2.5 Сложное движение точки
- •2.5.1 Относительное, переносное и абсолютное движения
- •2.5.2 Теорема о сложении скоростей
- •Пример 2.
- •2.5.3 Теорема о сложении ускорений (теорема Кориолиса)
- •2.6 Сложное движение твердого тела
- •2.6.1 Сложение поступательных движений
- •2.6.2 Сложение вращений вокруг двух параллельных осей
- •Рисунок 2.34 – Сложение однонаправленных параллельных вращений
- •2.6.3 Сложение вращений вокруг пересекающихся осей
- •Рисунок 2.36 – Сложение вращений вокруг пересекающихся осей
- •2.6.4 Сложение поступательного и вращательного движений. Винтовое движение
- •3 ДИНАМИКА
- •3.1 Введение в динамику. Законы динамики
- •3.2 Дифференциальные уравнения движения точки. Решение задач динамики точки
- •3.2.1 Основные соотношения
- •3.2.3 Последовательность и примеры решения задач
- •Пример 1.
- •Пример 2.
- •Пример 3
- •Рисунок 3.3 – Схема к задаче о движении лодки
- •3.2.4 Решение основной задачи динамики точки при криволинейном движении
- •Пример 1.
- •3.3 Общие теоремы динамики точки
- •3.3.1 Количество движения точки. Импульс силы
- •3.3.2 Теорема об изменении количества движения точки
- •Пример 1.
- •3.3.4 Движение под действием центральной силы. Закон площадей
- •3.3.5 Работа сил. Мощность
- •3.3.6 Примеры
- •3.3.7 Теорема об изменении кинетической энергии точки
- •Пример 1.
- •Пример 2.
- •3.4 Несвободное и относительное движения точки
- •3.4.1 Несвободное движение точки
- •Пример 1.
- •3.4.2 Относительное движение точки
- •3.5 Прямолинейные колебания точки
- •3.5.1 Свободные колебания без учета сил сопротивления
- •3.5.2 Свободные колебания при вязком сопротивлении
- •3.5.3 Вынужденные колебания. Резонанс
- •3.5.4 Вынужденные колебания при вязком сопротивлении
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ЛИТЕРАТУРЫ
- •ГЛОССАРИЙ
|
M0 |
h |
F |
|
|
adin |
M |
M1 |
 P
P
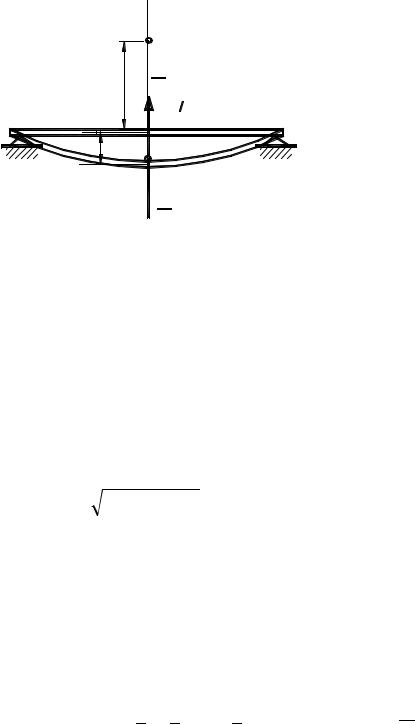
Рисунок 3.14 – К задаче о прогибе балки
Изменение кинетической энергии в данном случае равно нулю, так как и начальная скорость груза в точке М0, и конечная в точке М 1 равны нулю. Работа сил тяжести при падении груза равна Р·(h+adin), а запасаемая упругая энергия, работа сил упругости, равна –с·а2din/2; при нулевом изменении кинетической энергии сумма этих работ равна нулю:
P (h + adin ) −c adin2 / 2 = 0.
При статическом нагружении Р = с·аst , и тогда
adin2 − 2 ast adin − 2 h ast = 0. adin = ast ± 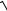
 ast2 + 2 h ast .
ast2 + 2 h ast .
При h = 0 получается adin = 2аst, т.е. динамическое приложение нагрузки вдвое увеличивает прогиб балки.
3.4 Несвободное и относительное движения точки
3.4.1 Несвободное движение точки
Рассмотрим движение точки М по гладкой заданной неподвижной
кривой под действием активных сил F1a , F2a , ... , Fna и реакции связи N .
Положение точки относительно начала отсчета О1 будем определять дуговой координатой s, отсчитываемой от точки О1. Проведем из точки М оси Мτnb, так что ось М τ направлена в сторону положительного направления отсчета s, Мn – вдоль главной нормали к центру кривизны траектории, Мb – по бинормали (рисунок 3.15). Для гладкой кривой ее реакция направлена по нормали к ней и лежит в плоскости Мbn. Поэтому Nτ = 0. В результате дифференциальные уравнения движения точки вдоль заданной будут иметь вид:
117

m |
dv |
a |
, |
или |
|
d 2s |
a |
; |
||
dt |
= ∑Fkτ |
m |
dt |
2 |
= Fkτ |
|||||
|
|
|
|
|
|
|
(3.28) |
|||
mv2 |
= ∑Fkna + Nn , |
0 = ∑Fkba + Nb. |
||||||||
|
||||||||||
ρ |
|
|
|
|
|
|
|
|
||
b
N O

 S
S
M
n
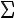 Fka
Fka
Рисунок 3.15 – Схема движения точки вдоль гладкой кривой
Из первого уравнения, где нет неизвестной реакции, можно определить закон движения точки вдоль кривой. Этим же уравнением можно пользоваться и при наличии трения, но тогда в первое уравнение войдет ила трения, выраженная через реакцию N. Два уравнения (оставшиеся) служат для определения реакции связи. Нужно отметить, что при криволинейном движении реакция связи зависит от скорости движения, в отличие от случая статики. Эту скорость, если она не задана, можно найти либо из уравнения (3.28), либо с помощью закона сохранения энергии, что обычно проще.
Пример 1.
Кольцу М массой m, нанизанному на горизонтально расположенную проволочную окружность, сообщается начальная скорость v0, направленная вдоль касательной к этой окружности (рисунок 3.16); на кольцо действует сила сопротивления F = kmv1/2, где k – постоянный коэффициент. Найти время, по истечении которого кольцо остановится.
Примем начало отсчета в начальном положении кольца. Уравнение движения кольца составим с учетом того, что сила тяжести P в него не войдет (она перпендикулярна оси Мτ и на движение кольца не влияет). То же относится и к реакции связи N .
118

m dv |
= −km |
|
; отсюда |
∫v |
dv |
|
= −k∫t |
dt, |
||
v |
||||||||||
|
|
|
||||||||
dt |
|
|
|
v0 |
|
v |
0 |
|
||
и 2(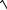
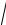 v0 −
v0 − 
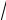 v) = kt.
v) = kt.
|
|
|
b |
|
|
N |
|
n |
C |
|
v |
|
|
||
|
O F |
s |
M |
|
|
||
|
|
P |
|
|
|
|
Рисунок 3.16 – Схема к задаче одвижении кольца по проволоке
В момент остановки t = t1, v = 0, тогда t1 = 2k v .
Время до остановки в этом примере является конечной величиной.
Пример 2.
Пусть в предыдущем примере сила сопротивления представляет собой силу трения F = f·N. Для конкретности R = 0,3 м, v0 = 2 м/с, f = 0,3. Какой путь до остановки пройдет кольцо?
Составляя уравнения (3.28), получим:
m |
dv |
= −F, |
mv2 |
= Nn , Nb = P. |
|
dt |
R |
||||
|
|
|
Сила трения
F = fN = f 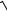
 Nb2 + Nn2 .
Nb2 + Nn2 .
Т.к. Nb = P = mg, то
F = fm g2 + v4 .
R2
Таким образом, сила трения зависит от скорости кольца. После замены dv/dt=v·dv/ds и сокращения на m получим уравнение движения в виде
119

v dv |
|
f |
|
|
|
= − |
|
g2R2 + v4 |
|||
R |
|||||
ds |
|
|
|
Разделяя переменные и беря в обеих частях равенства определенные интегралы, получим
v |
|
d(v2 ) |
|
|
|
f |
s |
||||
∫ |
|
|
|
|
|
|
|
|
= −2 |
|
∫ds, |
|
|
|
|
|
|
|
|
R |
|||
g |
2 |
R |
2 |
+ v |
4 |
||||||
v |
|
|
|
|
|
0 |
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
откуда
−2 fs / R = ln(v2 + 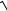
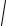 g2R2 + v4 ) −ln(v02 +
g2R2 + v4 ) −ln(v02 + 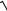
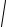 g2R2 + v04 )
g2R2 + v04 )
Окончательно
s = |
R |
ln |
v02 + |
g2R2 + v04 |
|
. |
||
2 f |
|
|
|
|
||||
v2 + |
g2R2 |
+ v4 |
||||||
|
|
|
|
|||||
В момент остановки v = 0, поэтому приближенно (считая g = 10 м/с2) получаем s ≈ 0,55 м.
Пример 3.
Груз весом Р висит на нитке длиной b. Его отклоняют на угол α и отпускают без начальной скорости. Определить натяжение нити в момент, когда груз будет в нижнем положении (рисунок 3.17).
|
|
n |
|
|
b |
T |
|
|
|
|
|
M0 |
|
h |
v1 |
|
M1 |
||
|
|
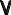 P
P
Рисунок 3.17 – К задаче об определении натяжения нити
Рассмотрим груз в нижнем положении. На него действуют сила
натяжения нити T и вес P . Радиус кривизны траектории определяется длиной нити b, и уравнение движения груза в проекции на нормаль к траектории n (в сторону вогнутости траектории)
mv2 |
/ b =T − P , или |
T = P + mv2 |
/ b, |
1 |
|
1 |
|
120

где v1 – скорость груза в нижнем положении. Для ее определения используем теорему об изменении кинетической энергии точки
mv212 − mv202 = Ph = Pb(1−cosα).
Поскольку v0 = 0, то mv12 = 2Pl(1−cosα), и окончательно получаем T
=P· (3–2cosα).
Вчастном случае, если нить в начальном положении отклонена на 90о, натяжение нити в нижней точке будет равно утроенному весу груза.
Пример 4.
Груз М подвешен на нити длиной b = ОМ (рис унок 3.18). Какую наименьшую скорость нужно сообщить грузу, чтобы он описал полную окружность в вертикальной плоскости?
|
|
M |
M1 |
|
|
|
|
n |
|
b |
O |
|
|
|
T |
|
|
M |
|
M0 |
v |
|
|
P 0 |
|
|
Рисунок 3.18 – К задаче о движении груза по полной окружности
Найдем натяжение нити в произвольном положении, определяемом углом ϕ, и будем исходить из того, чтобы при любом его значении натяжение нити было положительным. В положении М на груз действуют
сила натяжения нити T и вес P . Составим уравнение движения в проекции на главную нормаль Mn. Тогда
mv2/b = T – P·cosϕ, |
(3.29) |
где v – скорость груза в положении М. Для ее определения применяем теорему об изменении кинетической энергии:
mv2/2 – mv02/2 = – Ph = – Pb· (1–cosϕ).
Тогда
mv2 = mv02 – 2·P·b· (1–cosϕ).
Подставим это значение mv2 в (3.28) и вычислим Т:
121
