При описании движения планет это формулировка одного из законов Кеплера.
3.3.5 Работа сил. Мощность
Элементарной работой силы F называется скалярная величина dA = Fτ dS ,
где Fτ – проекция силы на касательную к траектории точки М, к которой приложена сила, dS – величина элементарного перемещения точки (рисунок 3.8). Т.к. Fτ = Fcosα, где α – угол междуF и Мτ, то
dA = F·dS·cosα. |
(3.21) |
F |
M1 |
Fn |
v |
|
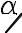ds F
M
M0
Рисунок 3.8 – К определению работы
В зависимости от значения угла α элементарная работа может быть положительной, отрицательной и равной нулю.
Поскольку dS = dr , выражение (3.21) можно представить в виде скалярного произведения
dA = F·dr – |
(3.22) |
элементарная работа равна скалярному произведению вектора силы на вектор элементарного перемещения точки ее приложения. В проекциях на оси координат (3.22) можно переписать как
dA = Fx·dx + Fy·dy + Fz·dz. |
(3.23) |
Здесь x, y, z – координаты точки приложения силы. Если точка прошла расстояние ММ1, то
111
M1 |
M1 |
|
||
A = ∫ |
Fτ ds = ∫ |
(Fxdx + Fydy + Fzdz). |
(3.24) |
|
M |
|
M |
|
|
Интеграл берется вдоль кривой ММ1 и является криволинейным.
В частном случае, когда сила постоянна, а траектория прямолинейна, и сила направлена вдоль траектории:
A = FS. [ A ] = Дж = Н·м =…
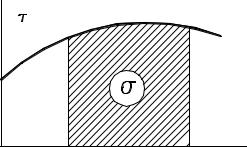
Геометрический смысл интеграла (3.24) – площадь σ под кривой зависимости силы от пути (рисунок 3.9).
|
F |
|
|
0 |
|
S |
|
S |
S1 |
||
|
|||
Рисунок 3.9 – Работа сил |
|||
Мощностью называется скалярная величина
N = dA |
= F ds |
= F v. |
(3.25) |
dt |
τ dt |
τ |
|
Мощность равна произведению касательной составляющей силы на скорость точки приложения силы.
[ N ] = Ватт=Дж/с=…
Из (3.25) ясно, что если мощность (например, двигателя) постоянна, то для выигрыша в силе нужно уменьшить скорость движения.
3.3.6Примеры
1.Работа силы тяжести
Пусть точка М под действием силы тяжести Р перемещается из положения М0(x0,y0,z0) в положение М1(x1,y1,z1). Направим ось Oz вертикально вверх (рисунок 3.10). Тогда
Рх = Ру = 0, Pz = – P.
112
|
Z |
M0 |
|
|
|
|
|
M |
|
|
|
|
h |
z0 |
|
|
|
|
|
|
|
M1 |
|
|
0 y |
x0 |
P |
z1 |
Y |
|
|
x1 |
|
||
X |
0 |
y1 |
|
|
|
|
|
|
|
||
Рисунок 3.10 – К задаче о работе сил тяжести |
|||||
Из (3.24) следует
z1
A = ∫(−P)dz = P(z0 − z1).
z0
Обозначим h = z0 – z1, тогда A = Ph.
Если z0 > z1, h > 0, то A > 0, т.е. работа положительна.
Как видно из этих выкладок, работа силы тяжести зависит только от соотношения начальной и конечной высот и не связана с формой траектории перемещения.
Силы, для которых работа не зависит от траектории, а |
||
определяется только начальным и конечным положением перемещаемого |
||
объекта, называются потенциальными. |
|
|
2. |
Работа силы упругости |
|
|
x1 |
|
|
x0 |
|
|
F |
M X |
|
|
|
|
O |
|
|
Рисунок 3.11 – К задаче о работе сил упругости |
|
Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к концу пружины (рисунок 3.11). В этом случае сила упругости пружины линейно связана с перемещением вдоль х: Fx = – cx; это равенство справедливо как при положительных значениях х, так и отрицательных. Знак минус свидетельствует о том, что пружина всегда
113