Если ϕ = const, то (2.26) представляют собой уравнения поступательного движения АТТ.
Если xA = const, yA = const, то (2.26) определяет вращение плоской фигуры вокруг точки А (или вращение АТТ вокруг оси, проходящей через точку А перпендикулярно плоскости этой плоской фигуры).
Таким образом, в общем случае движение плоской фигуры в ее плоскости слагается из поступательного движения полюса и вращения фигуры вокруг этого полюса.
Характеристиками плоского движения являются: скорость и ускорение поступательного движения полюса А и угловые скорость и ускорение вращательного движения вокруг этого полюса.
Все эти величины и определяются из уравнений движения (2.26). В качестве полюса можно выбрать любую точку фигуры. При этом
характеристики поступательного движения в общем случае изменятся (только в том случае, когда тело движется поступательно, изменение полюса не приведет к изменению уравнения его движения). Что касается вращательного движения, оно не меняется. Это усматривается из следующего рассуждения: если из точки С (нового полюса) провести
прямую CD AB, то эти прямые всегда параллельны. Но это и означает, что вращательное движение не зависит от выбора полюса.
2.3.2 Определение траекторий точек плоской фигуры
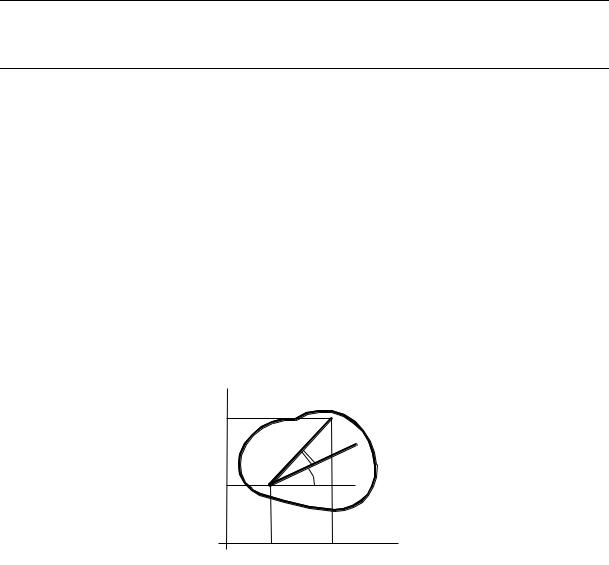
Рассмотрим точку М плоской фигуры, так что угол МАВ = α, а расстояние АМ = b (рисунок 2.15).
y |
x |
|
M |
|
|
|
|
||
|
|
|
B |
|
|
|
|
α |
|
|
xA A |
|
β |
|
|
yA |
|
|
|
O |
|
y |
|
|
|
|
|
||
|
|
|
|
|
Рисунок 2.15 – К определению траекторий точек тела |
||||
Для точки М: |
|
|
|
|
xM = xA +b cos(ϕ+α), |
yM = yA + b sin(ϕ+α). |
(2.27) |
||
В этих уравнениях величины xA, yA, ϕ известны из (2.26). По |
||||
существу, зависимости (2.27) |
|
и есть уравнение |
траектории в |
|
|
|
|
|
69 |