2.2.3 Равномерное и равнопеременное вращения

Если угловая скорость постоянна, вращение тела называется равномерным. Тогда из соотношения

dϕ/dt = ω

следует

ϕ= ϕ0 + ωt.

ϕ= ωt, ω = ϕ/t при ϕ0 = 0.

Втехнике часто используют для измерения угловой скорости внесистемную единицу – обороты в минуту. Для перехода к с–1 нужно использовать формулу

ω= 2π n/60 ≈ 0,1 n,

где n выражено в об/мин.

Вращение тела называется равнопеременным, если угловое ускорение постоянно: ε = const.

Тогда

ω = ω0 + εt, ϕ = ϕ0 + ωt + εt2/2.

Аналогия с равноускоренным поступательным движением очевидна: зависимость угловой скорости от углового ускорения такая же, как зависимость линейной скорости от линейного ускорения. То же справедливо и для угла поворота как функции времени– зависимость точно такая же, как пройденного пути от времени в случае поступательного движения тела, с точностью до обозначений.

2.2.4 Скорости и ускорения точек вращающегося тела

Если точка АТТ находится на расстоянии h от оси вращения, а тело за время dt поворачивается на угол dϕ, то скорость движения этой точки определяется как

v = h dϕ/dt = hω.

Для v обычно используется термин «линейная» или «окружная» скорость точки М. Числовое значение скорости точки вращающегося тела равно произведению угловой скорости на расстояние от точки до оси вращения.

Линейная скорость v направлена по касательной к окружности, перпендикулярно плоскости, проходящей через точку и ось вращения. Т.к.

64

угловая скорость одинакова для всех точек тела, то скорости точек вращающегося тела пропорциональны расстоянию от них до оси.

Ускорение точек тела получается из формул aτ = dv/dt, an = v2 / ρ.

Тогда

aτ = hdv/dt = hε, an = h2ω2/h = hω2.

Ускорение aτ направлено по касательной к окружности, при

ускоренном вращении – в сторону движения.

Ускорение an всегда направлено по радиусу к оси вращения.

Таким образом, касательное и нормальное ускорения всегда ориентированы взаимно перпендикулярно, поэтому величина полного ускорения определяется по формуле:

a = h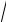ε2 + ω4 .

Отклонение вектора полного ускорения a от радиального направления определяется углом

tgµ = aτ = ε2 . an ω

Т.к. ε и ω одинаковы для всех точек тела, то ускорения всех точек тела пропорциональны h, и угол, составляемый вектором полного ускорения a с радиусом, одинаков для всех точек.

Таким образом, зная закон движения одной любой точки тела, вращающегося вокруг неподвижной оси, мы можем определить эти законы для любых точек тела.

Если возьмем начало координат на оси вращения, и обозначим r – радиус-вектор, то (рисунок 2.12)

h = |r | sin α,

тогда

v = ωh = ωr sin α.

65

B

A

Рисунок 2.12 – Определение вектора скорости точки вращающегося тела

т.е вектор скорости любой точки вращающегося тела равен

векторному произведению угловой скорости тела на радиус-вектор этой точки. Соотношение (2.23) иногда называют формулой Эйлера.

В этом выражении первое слагаемое представляет собой вектор, направленный так же, как ω×r , – по касательной к траектории. При этом

ε×r εr sin α = εh.

Следовательно, первое слагаемое является касательным ускорением

aτ .

Второе слагаемое ω×v направлено по радиусу (поскольку ω направлено вдоль оси, v – по касательной), при этом

ω×v = ωv sin900 = ωv = ωh2 ,,

т.к. v = ωh. Таким образом, второе слагаемое представляет собой нормальное ускорение an .

Пример 1.

66