Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика (семестр 2, часть 2).-1

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

641.56 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

z n

z 2

z 3

Итак,

z 2

2 n 0

2 4

есть требуемое разложение в степенной ряд Тейлора.

Задача 8. Разложить в ряд Тейлора	f (z)	z

		(z 1)( z 3)
и найти f ( 4) (0) .

z 4 ... это и 16

по степеням z

Решение. В этой задаче сначала надо разложить на простейшие, чтобы в каждой дроби в знаменателе была только сумма или разность двух объектов.

f (z)

A(z 3) B(z 1)

, тогда

1)( z 3)

(z 1)( z 3)

Az 3A Bz B 1z 0 система

A B 1

4A 1

3A B 0

. Тогда функция имеет вид

1 1

4 z 1

4 z 3

Точки разрыва z 1 и z 3, поэтому наибольший круг с центром в нуле может быть радиуса 1. Итак, ряд будет существовать в круге

1. При этом очевидно, что

1 3 , поэтому автоматически

выполнено и условие

3 , т.е.

1. Поэтому во второй дроби

можно выносить 3 за скобку для формирования структуры суммы

прогрессии вида											1		. Итак,			1	1			3	1		=
прогрессии вида									1		q		. Итак,			4 z 1				4 z 3			=
									1		q					4 z 1				4 z 3
	1 1			3		1		1			=			1	1		3 1		1				=
											=												=
	4 1 z 4 3									z				4 1 z 4 3								z
							1											1
									3

																						3
	1		n		1							z n
		z											. Можно объединить эти две суммы в одну.
		z											. Можно объединить эти две суммы в одну.
	4 n 0				4 n 0							3

1		( 1)n			n
	1				n	.
	1	3	n	z		.
4 n 0		3

Теперь найдѐм коэффициент при 4 степени, чтобы найти f ( 4) (0) . Приравняем коэффициент из этого ряда и тот его вид, который

	1		( 1)		4	f (4) (0)
следует из теории.		1					тогда
следует из теории.		1		4			тогда
	4		3	4		4!
	4		3			4!

	(4)		4!		( 1)		4			1		6 80		160
f		(0)		1				= 6	1		=		=		.
f		(0)		1		4		= 6	1		=		=		.
			4		3	4				81		81		27
			4		3					81		81		27

1			( 1)n		n			( 4)		160
		1					f		(0) =
Ответ. Ряд			3	n z		,				27	.
	4 n 0
Задача 9. Найти		f (10) (0)		для	f (x) xsin x .

Решение. Рассмотрим разложение в ряд Тейлора. Прогрессия здесь не нужна, можно воспользоваться известной формулой для синуса.

xsin x = x x

...

= x 2

...

Здесь нам нужен только коэффициент при степени 10.

f (10) (0)

10!

10 .

10!

0,1

Задача 10. Приближѐнно найти значение интеграла

sin(x2 )dx с

точность 10 5 .

Решение. Разложим функцию под интегралом в ряд.


0,1										0,1								(x		2	)	3		(x			2		)	5								0,1								x	6			x	10
	sin(x				2	)dx =									2			(x			)			(x					)													2				x				x
	sin(x					)dx =								(x		)			3!							5!					... dx =									x					3!					5!		... dx
0													0						3!							5!												0							3!					5!
=		x3		0,1					x7				0,1			x11			0,1		...			Видно, что даже второе слагаемое
		x3							x7				0,1			x11			0,1
								7 3!							11 5!
3				0				7 3!					0		11 5!				0
				0									0						0
меньше, чем 10 7 , то есть может повлиять лишь на 6 знак после
запятой.							x3				0,1			0,001				0,00033 .
							x3				0,1			0,001

						3					0				3
											0				f (8) (0) для									f (z) 2x3 sin											x
Задача 11. Найти																																			x		.
Задача 11. Найти																																			2		.
																																			2
																																		x	3				x				5
																																		x					x

																												x
Решение. f (z) 2x																3			x						3			x						2						2
																	sin				= 2x																							...					=
																	sin				= 2x																							...					=
																			2									2						3!						5!


	x 4				x6								x8
															...			Извлекаем слагаемое при степени 8 и
					2							24			...			Извлекаем слагаемое при степени 8 и
			2		2	3!						24		5!
сравниваем его с теоретическим значением.
	f (8) (0)									1				f (8) (0)											8!						=		6 7 8				=	6 7 23								=		42		21 .
8!										4 5!				f (8) (0)									24								=			24			=			24						=			2	21 .
8!						2				4 5!													24					5!						24						24									2
Ответ.						f (8) (0) = 21.
Задача 12. Разложить в ряд Тейлора:																																f (z)									z								по

																																				(z 1)( z 3)

степеням z 1.

Решение. Разложение на простейшие сначала производится точно так

же, как в задаче 8:	1 1	3 1	. Но здесь центр круга не в 0, а в

	4 z 1	4 z 3
	4 z 1	4 z 3

точке 1 потому что z 1 z ( 1) . Точки разрыва z 1 и z 3.

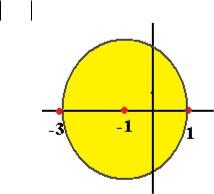
Поэтому расстояние до ближайшей точки разрыва равно 2, и круг здесь имеет вид z 1 2 . Он показан на чертеже:

В выражении													1		1					3			1		сначала надо прибавить и отнять
В выражении													4 z					1		4 z 3					сначала надо прибавить и отнять
													4 z					1		4 z 3
константы, чтобы в знаменателе явно был выделен блок z 1.
	1				1				3		1			=		1						1				3		1			теперь скобку вида (z 1)
	4 z 1								4 z 3					=			4 (z 1) 2									4 (z 1)				2	теперь скобку вида (z 1)
	4 z 1								4 z 3								4 (z 1) 2									4 (z 1)				2
мы не будем раскрывать вплоть до ответа, можно даже
переобозначить еѐ через w (но не обязательно).
Выносим за скобку константу 2 в каждой из дробей.
				1			1					3			1												z 1		2 получается, что верно
				1			1					3			1						. В круге
				8 1			z			1		8 1					z 1				. В круге
							z			1							z 1

								2										2
		z 1				1 то есть там как раз получается такое q 1, как и надо для
		z 1

			2
			2
сходящейся геометрической прогрессии. Тогда далее
			1				1					3						1								1		z 1 n				3	z 1	n
																								=										.
							z 1												z 1					=										.
			8				z 1					8							z 1							8 n 0 2						8 n 0	2
					1			2						1												8 n 0 2						8 n 0
					1									1
																				2

Здесь в 2 частях индексы меняются синхронно, т.е. можно объединить

	1 3( 1)	n	z 1 n .
	1 3( 1)		z 1 n .
n 0	2n 3

Задача 13. Разложить в ряд Тейлора: f (z)	z 2	по степеням z.
	z2 1

Решение. Сначала надо разложить на простейшие дроби.

f (z)

z 2

A(z 1) B(z 1)

z2 1

z 1

(z 1)( z 1)

A B 1

Az A Bz B 1z 2 система

B 2

2A 3

Итак, функция имеет вид:

3 1

2 (z 1)

Теперь оценим, в каком круге будет разложение. Центр в 0, так как по степеням z. Точки разрыва z 1, z 1. Расстояние от центра до ближайшей точки разрыва равно 1. Поэтому разложение в ряд будет в

круге

3 1

1 1

3 1

1 1

теперь то, что следует в

2 z 1

2 1 z

2 1 (z)

знаменателе после единицы, уже и так удовлетворяет условию z 1,

то есть выносить за скобки никакие константы уже не надо. Можно уже использовать формулу суммы прогрессии.

													( 1)	n
	3	1	1	1		=	3	z n		1	( z)n	= 3	( 1)	z n =
	2 1 z		2 1 (z)				2	n 0		2	n 0	n 0	2
								n 0			n 0	n 0
2 z 2z 2 z3					...
445 ПРАКТИКА № 13								20.05.2016
Задача 1. Найти производную									f (6) (0) для			f (x) e x sin x .

Решение. Запишем разложения в ряд Тейлора для каждой функции.

f (x) 1 x

... x

...

Найдѐм все те комбинации, которые дают 6 степень.

		x5	x3			x3				x5					2		1		6											f (6) (0)		6
	x											x		=				x		, что надо приравнять к											x		.
		5!		3!	3!				5!						5!	3!3!														6!
	f (6) (0)				2				1				2			1	=	1			1	6 10					4		1	.
																	=													.
		6!			5!			3!3!					120			36		60			36	360				360			90
	f (6) (0)						6!				720				8.
	f (6) (0)														8.
					90						90
																								z	n
Задача 2. Найти кольцо сх ряда Лорана:																								z
Задача 2. Найти кольцо сх ряда Лорана:																							1			3		n
																						n	1			3
																						n

Решение. Сначала исследуем правильную часть.

n 1

1 3

, по признаку Даламбера lim

lim

n 0 1

n 1 3n 1

сократим на 3n числитель и знаменатель.

0 1

1, тогда

3 .

lim

0 3

Теперь рассмотрим главную часть

. Можно задать

n 1

индексацию натуральными числами, если сделать замену m n и после этого уже применять обычный признак Даламбера.

	1			z	n					z	m								1
				z		=				z			=						1					.
			1		3n	=			1	3 m			=					m				1		.
n			1		3n			m 1	1	3 m					m 1 z			m				1
																		1
																		1
																					3m
																m			1											1
																m			1											1
															z		1											1
																				m
																															m
Тогда				lim						1								3					=		1		lim			3	m	=
										1								3							1					3
								m 1				1						1								z				1
				m																							m	1
				m																							m
							z		1
							z		1			3m 1																	3m 1
	1 1 0
						1
						1		1 , тогда					z	1.

	z	1 0				z

Ответ 1

3 - кольцо сходимости.

Задача 3. Разложить в ряд Лорана

f (z)

по степеням z

z 3

z 4

Решение. Точки разрыва z 3

и z 4 , центр кольца в 0, значит,

кольцо определяется условием 3

4 .

z n

1 1

f (z)

z 3

z n 0 z

4 n 0

( 1)n

. Можно ещѐ произвести сдвиг индекса в

n 1

n 0 z

n 0

главной части, чтобы не был индекс 0 в двух частях сразу:

n 1

( 1)n

но фактически и так было видно, что главная

n 1

n 0

часть начинается с -1 степени.

Задача 4. Разложить в ряд Лорана

f (z)

по степеням

z 3

z 4

(z 1) в кольце.

Решение. В отличие от прошлой задачи, здесь центр смещѐн в 1. Это влияет и на радиусы кольца. Ближайшая точка разрыва на расстоянии 2, а более далѐкая на расстоянии 5. Поэтому условие кольца

2 z 1 5. Но сначала надо прибавить и отнять 1, чтобы создать

отдельное слагаемое z 1 его мы не будет раскрывать вплоть до ответа.

	1	1			1	1
f (z)				=			теперь выносим за скобку
	z 3		z 4		(z 1) 2	(z 1) 5

либо константу, либо z 1 с учѐтом того, что должно получаться 1 и второй объект, который меньше 1.

1		1			1		1		согласно условию 2	z 1	5 , каждый
1		1			1		1
z 1				2	5			z 1
z 1				2	5			z 1
	1					1
			z	1

								5

объект в знаменателе здесь по модулю меньше 1 и может служить знаменателем сходящейся геометрической прогрессии.

(z 1)

Далее,

( 1)n

z 1 n 0

(z 1)n

5 n 0

(z 1)

( 1)n

(z 1)n 1

n 0

5n 1

Задача 5. Разложить в ряд Лорана

f (z)

во внешней

z 3

z 4

области

z 1

5 .

Решение. Здесь z 1 5 , а значит атоматически и z 1 2 . Поэтому

выносить за скобку в знаменателе надо так, чтобы всегда получались константы, делѐнные на z 1.

1					1				1		1				1			1
							=													=
(z 1) 2				(z 1) 5			=		z 1				2			z 1			5	=
										1							1
													1
												z							z 1
												z							z 1
1		2	n			1					5			n
1		2				1		( 1)n			5
								( 1)n
z 1 n 0	(z 1)n					z 1 n 0					(z 1)n

Первая часть преобразуется, как и в прошлом примере, а вот вторая по-новому. Кстати, здесь можно объединить, так как обе суммы относятся к главной части, там везде отрицательные степени.

1	( 1)	n	5	n	2	n		( 1)	n	5	n	2	n
							=							.
z 1 n 0	(z 1)n						n 0	(z 1)n 1

45 минут контрольная № 3. Темы:

1.Действия с комплексными числами.

2.Формула Муавра.

3.Числовые ряды.

4.Функциональные ряды.

Пример. Контрольная работа №3. Вариант № 0.

1. Поделить 1 5i .

1 7i

2. Вычислить в показательной форме: (3 i)9 ответ дать в виде a+bi.

				n			n
3.	Исследовать сходимость ряда	( 1)			2
3.	Исследовать сходимость ряда
	n 1		n!
	n 1
			(x 2)n
4.	Найти область сходимости ряда
4.	Найти область сходимости ряда			3		n
	n 1			3
445 ПРАКТИКА № 14 27.05.2016			Ряды Фурье.

Задача 1. Разложить в тригонометрический ряд Фурье функцию f (x) x на (-1,1).

Решение. Так как функция нечѐтная, то все коэффициенты a0 и an равны 0. Поэтому считаем только bn . Учитываем, что l 1.

1 1

bn 1 1x sin n xdx . Вычисляем интеграл по частям.

u x ,

u 1,

v sin n x , v

cosn x . Тогда

cosn x

1 cosn xdx =

cosn

cos(n )

sin n x

так как косинус чѐтная

n2 2

функция, то

cosn

(0 0) =

cosn =

n2 2

2( 1)

n 1

Ответ. 2( 1)

sin n x .

= 2( 1)

n 1

Задача 2. Разложить в триг. ряд Фурье f (x) 2x 3 на (-1,1) Решение. Заметим, что функция f (x) 3 2x нечѐтная. То есть, f это

сумма нечѐтной и константы. Таким образом, коэффициенты an

здесь

тоже окажутся равны 0. Надо вычислить a0

и bn .

1 = (1 3) (1 3) 4 ( 2) 6 ,

(2x 3)dx = (x2

3x)

3 .

(2x 3) sin n xdx

. Вычисляем интеграл по частям.

u 2x 3 ,

u 2 ,

v sin n x ,

cosn x . Тогда

2x 3

cosn x

cosn xdx =

cosn

cos(n )

sin n x

n2 2

4( 1)n

4( 1)n 1

cosn

(0 0) =

cosn

n 1

Ответ. Ряд Фурье:

4( 1)

sin n x .

n 1

Замечание. Для поиска коэффициентов bn можно было

воспользоваться результатом, полученным в задаче 1.

(2x 3) sin n xdx = 2 x sin n xdx 3 sin n xdx

первое слагаемое содержит интеграл, равный в итоге

2( 1)n 1

4( 1)n 1

второе равно 0. Тогда

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023232.93 Кб4Маркетинговые исследования.-1.pdf
#
05.02.2023396.22 Кб2Маркетинговые исследования.-2.pdf
#
05.02.20231.34 Mб3Маркетинговые исследования.-3.pdf
#
05.02.20231.35 Mб3Маркетинговые исследования..pdf
#
05.02.20231.3 Mб5Математика (семестр 2, часть 1)..pdf
#
05.02.2023641.56 Кб2Математика (семестр 2, часть 2).-1.pdf
#
05.02.2023938.68 Кб3Математика (семестр 2, часть 2)..pdf
#
05.02.2023722.47 Кб5Математика 3 семестр..pdf
#
05.02.20231.9 Mб20Математика для гуманитарных, экологических и экономико-юридических специальностей. Часть 1.pdf
#
05.02.20234.98 Mб6Математика для гуманитарных, экологических и экономико-юридических специальностей. Часть 2.pdf
#
05.02.202311.03 Mб10Математика-2-й семестр (курс лекций)..pdf