
Электромагнитные поля и волны.-5
.pdf
79
51. Электрон, летящий вдоль оси Z со скоростью V = 106 м/с, попадает в зону, где одновременно существуют стационарное электрическое и магнитное поля, имеющие вид: E = xa E x и B = y0 By ,
где Еx = 1 103 В/м;
Вy = 4мТл. Определить величину силы, воздействующей на электрон.
Ответ: F=e·3·103, H.
52. В сферическом объёме радиуса R равномерно распределён гармонически изменяющийся заряд с объёмной плотностью ρ =1cos ω t. Чему будет равен ток проводимости, связанный с этим зарядом?
Ответ: I пр = 4 πR3ω sin ω t
3
53. Среды разделены заряженной поверхностью, и в одной из них поле отсутствует. Каково электрическое поле в другой среде, если поверхностная плотность заряда ξs, а диэлектрическая проницаемость второй среды ε2.
Ответ: Е= ξs/(2εr2)
54. Вектор D направлен под углом 450 к границе раздела двух сред диэлектрические проницаемости которых равны ε1=1, ε 2 = 
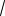 3 .
3 .
Поверхностная плотность заряда ξ=0. Определить угол α2 между D 2 и границей раздела.
Ответ: α 2 = 300 .
55.Относительная диэлектрическая проницаемость среды
изотропного диэлектрика равна |
ε r |
= 9 . Чему равна электрическая |
||||||||
восприимчивость? |
|
|
|
|
|
|
|
|
|
|
Ответ: 8 |
|
|
|
|
|
|
|
|
|
|
56. К неоднородному |
диэлектрику |
с |
параметром |
ε = ε 0 (1 + x) 2 |
||||||
приложено электрическое |
поле |
R |
R |
|
R |
|
|
выражение |
||
|
|
|
|
|||||||
E = Ex x 0 |
+ Ez z 0 . Какое |
|||||||||
будет у вектора электрического смещения? |
|
|
|
|
||||||
Ответ: () ε0 (1 + х) |
2 |
|
R |
R |
R |
|
0 ×(1 + х) |
2 |
R |
|
|
= . E = (Ex x0 + Ez z0 ) ×ε |
|
= D. |
|
||||||
80
57. По границе раздела сред протекает поверхностный ток ηRS . В
первой среде H = 0 . Определить магнитное поле во второй среде вблизи поверхности.
Ответ : ηRS /2
2.4.Контрольные вопросы
1.Как математически выразить непрерывность линии вектора
а?
2.Укажите размерность результата rotH = 5x° .
3.Какой ток течет в пространстве диода, к электродам которого подведено напряжение (быстропеременное)?
4.Укажите зависимость между плотностью тока проводимости и самим током проводимости.
5 Что определяет выражение ∫rotHdS ?
S
6 Как определяется анизотропность среды?
7.Укажите систему уравнений электромагнитного поля, не зависящего от времени в проводящей среде без сторонних токов и зарядов.
8.Какое физическое толкование может быть дано уравнению
rotH = 10z° ?
9.Укажите тензор магнитной проницаемости.
10. Укажите математическое выражение теоремы Стокса.
11.Каково направление потока вектора электрической индукции∫DdS = −10k ?
S
12.Что представляет тензор удельной проводимости?
13.Какие токи возможны в среде с параметрами ε, μ и σ=0?
14.Укажите размерность в уравнении rotE = − ∂B .
∂t

81
15. Укажите проекцию плотности тока проводимости δ пр на ось z, исходя из уравнения закона Ома δпр = σˆE , если в анизотропной
σ κH 0
среде σ = -κH |
σ |
0 . |
ˆ |
|
|
0 |
0 |
σ Z |
16. Каковы виды токов, которые могут иметь место в идеальном диэлектрике?
17.Укажите символическое определение первого уравнения Максвелла.
18.Каков физический смысл третьего уравнения Максвелла
∫DdS = 0 ?
S
19.Укажите зависимость между плотностью тока проводимости и самим током проводимости.
20.Какова размерность в уравнении divB = 0 ?
21.Что нужно знать, чтобы определить величину тока проводимости, пересекающего поверхность S ?
22. Укажите размерность уравнения divD = 0 . Ф × В/ м3 . 23.Укажите математическую запись закона электромагнитной
индукции.
24.Укажите проекцию rotH = δ пол на ось у.
25. Укажите проекцию rotE = − ∂B на ось х.
∂t
26.Как называются среды, в которых один из параметров ε, μ и σ зависят от координат?
27.Укажите третье уравнение Максвелла, записанное в декартовых координатах.
28. Укажите математическую запись закона полного тока.
29.Укажите математическую запись постулата Максвелла. 30.Укажите запись теоремы Остроградского-Гаусса. 31.Укажите закон Ома в дифференциальном виде.
32.Чему равен поток вектора D через поверхность S , изображенную на рисунке?
33.Укажите проекцию вектора В на ось у, используя материальное уравнение.
34.Укажите уравнение, выражающее закон сохранения заряда.

82
Глава 3. Электростатическое поле
Целью данного занятия является закрепление теоретического материала путем решения задач по следующим вопросам курса:
Электростатические поля, создаваемые заряженными телами. Силы в электростатических полях.
3.1. Краткие теоретические сведения
Электростатическое поле описывается системой дифференциальных и интегральных уравнений, которые являются частным случаем общих уравнений Максвелла (2.1)÷(2.6) в предположении, что создающие его заряды не зависят от времени и не перемещаются в пространстве [1].
Интегральные уравнения: |
Дифференциальные |
|
|
|
уравнения: |
∫ Ed l = 0 ; (3.1) |
rotE = 0 ; (3.1а) |
|
e |
|
|
∫ DdS = ∫ ρdV = q ; (3.2) |
divD = ρ (3.2а) |
|
S |
V |
|
материальное уравнение D = ε E (3.3)
3.1.1. Электростатический потенциал
Непосредственно из уравнений Максвелла ( rotE = 0 ) следует, что электрическое поле является потенциальным, следовательно, его силовые линии начинаются и оканчиваются на зарядах и вектор напряженности электрического поля может быть представлен градиентом потенциала.
R |
− ϕ2 |
|
Ì 2 R R |
|
E = −gradϕ , ϕi |
= |
∫ EdL . |
(3.4) |
|
|
|
|
M1 |
|
R
Уравнение (3.2а) с учетом (3.3) принимает вид divε E = ρ .
R
Подстановка E в форме градиента потенциала в уравнение
(3.2а)
приводит к уравнению Пуассона, которое является основным
уравнением для нахождения потенциала: div(ε gradϕ) = −ρ .
83
Для однородной среды уравнение Пуассона принимает вид объемного заряда,
divgradj = Ñ2j = -r/ e . |
(3.5) |
Для неоднородной среды, при равенстве |
нулю объёмного |
заряда уравнение Пуассона преобразуется в уравнение Лапласа.
|
|
|
div (ε grad ϕ) = 0 |
|
|
|
|
(3.5а) |
||
Уравнения Пуассона и Лапласа дополняются граничными |
||||||||||
условиями на границах раздела сред: |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
Условия на границе металл |
Условия |
на |
границе двух |
|||||||
– диэлектрик (М-Д) |
диэлектриков (Д-Д) |
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
Eτ = 0, |
|
|
Eτ |
= Eτ |
2 |
, |
|
||
1 |
ϕìåò |
= const |
|
1 |
|
|
|
|
||
|
ϕ1 = ϕ2 (3.8) |
|
||||||||
|
(3.6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
D = ξ, |
|
|
Dn1 |
− Dn2 |
|
= ξ |
|
||
|
n |
|
|
|
|
|
|
|
|
|
2 |
∂ϕ |
= ξ |
(3.7) |
|
Dn |
= Dn |
|
|
при ξ = 0 |
|
|
ε1 ∂n |
|
|
1 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
∂ϕ1 |
|
|
∂ϕ2 |
= −ξ (3.9) |
|
|
|
|
|
|
ε1 ∂n − ε2 |
∂n |
||||
Уравнения Пуассона и Лапласа применяются для решения краевых задач, в которых на электродах, расположенных в диэлектрике, заданы потенциалы или заряды и требуется определить электрическое поле в этом диэлектрике.
Существует широкий класс задач, в которых требуется определить поле по известному распределению зарядов. При решении таких задач большое значение имеют понятия: точечный заряд q , заряженная нить, поверхностный заряд ξ , объемный заряд
ρ .
Точечным зарядом можно считать заряд q , расположенный на теле, линейными размерами которого можно пренебречь.
Под заряженной нитью понимают бесконечно длинный и тонкий проводник, имеющий линейную плотность заряда τ .
Если заряды распределены в пространстве дискретно или непрерывно, то в некоторой точке суммарному заряду соответствует суммарный потенциал (принцип суперпозиции).

84
На основании принципа суперпозиции решение уравнения Пуассона имеет вид:
для |
распределенного |
|
ϕ = |
1 |
V∫ |
ρdv |
|
||||||||||||
объемного заряда |
|
|
|
|
|
|
|
|
4πε |
r |
(3.10) |
||||||||
для |
заряженной |
|
|
|
|
1 |
|
|
|
τ dl |
|
||||||||
|
|
φ = |
|
|
|
|
∫l |
|
|
|
|||||||||
цилиндрической поверхности |
|
|
4πε |
r |
(3.11) |
||||||||||||||
конечных размеров |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для |
поверхностных |
|
ϕ = |
1 |
|
∫ |
ξ |
dS |
|
||||||||||
зарядов |
|
|
|
|
|
|
4πε |
r |
(3.12) |
||||||||||
|
|
|
|
|
|
|
|
|
S |
|
|
||||||||
для точечных дискретных |
|
ϕ = |
1 |
|
|
n |
qi |
|
|
||||||||||
зарядов |
|
|
|
|
|
|
4πε |
∑i=1 ri |
(3.13) |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Напряженность электрического поля и потенциал, создаваемые |
|||||||||||||||||||
точечным зарядом |
|
|
r τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
R |
= |
и ϕ = |
|
q |
|
|
. |
|
|
|
|
|
|
(3.14) |
|||
|
E |
0 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
4πε r 2 |
4πε r |
|
|
|
|
|
||||||||||||
Напряженность электрического поля и потенциал, создаваемые |
|||||||||||||||||||
заряженной нитью |
|
r τ |
|
τ |
|
|
|
|
|
|
|
|
|
|
|||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
E = |
0 |
и |
ϕ = |
|
ln r + C |
. |
|
|
(3.15) |
|||||||||
|
|
|
|
||||||||||||||||
|
2πε r 2 |
2πε |
|
|
|||||||||||||||
3.1.2. Энергия электростатического поля. Емкость. Силы в электростатическом поле
Энергия электростатического поля может быть определена
через плотность энергии электрического поля ωý = 1 ε Å 2 путём
2
интегрирования её по объёму
|
|
|
|
Wý |
= ∫ ωý |
dv |
|
(3.16) |
|
|
|
|
|
V |
|
|
|
или через потенциал и заряды: |
|
|
|
|
||||
WÝ |
= |
1 |
qϕ |
, Wý = ∫ ρϕdv , Wý |
= ∫ξ sϕds |
, Wý = ∫τϕdL . |
(3.17) |
|
|
||||||||
|
2 |
|
V |
|
s |
l |
|
|
|
|
|
|
|
|
|||
Формулы |
|
для |
расчета |
энергии |
электрического |
поля |
||
соответствующие случаям (3.10)÷(3.13) приведены ниже:
85
Wэ = |
1 |
∫ ρϕdv , Wý |
= |
|
1 |
∫τϕdv , |
|||
2 |
2 |
||||||||
|
|
|
|
|
|
|
|
|
V |
|
|
1 |
|
|
|
1 |
n |
||
Wý |
= |
|
ξs dS и Wý |
= |
∑ϕi qi . |
||||
|
|
|
|||||||
|
2 |
∫S |
|
|
2 i=1 |
||||
В последней формуле случае не учтены взаимодействия заряженных тел.
Емкость системы, состоящей из двух заряженных проводников определяется как отношение заряда одного из проводников к разности потенциалов между ними
C = |
|
q |
|
(3.18) |
|
−U |
|
||
U1 |
2 |
|
||
Сила, действующая на точечный заряд q , помещённый в электростатическое поле, равна
R R
F = qE ,
Сила взаимодействия двух точечных зарядов на расстоянии r12 друг от друга, определяют с Кулона:
R |
R |
0 |
q q |
2 |
F |
= r |
1 |
||
|
4πε r12 |
|||
|
|
|
||
(3.19) q1 и q2 отстоящих помощью закона
(3.20)
Сила, действующая на заряженную поверхность при равномерно распределённом заряде
R |
R |
(3.21) |
F |
= ξS SE , |
где S-площадь заряженной поверхности.
3.2. Примеры расчета электростатических полей
Однородные задачи электростатики. Определение потенциала плоских и сферических конденсаторов
Коднородным задачам электростатики относятся такие задачи,
вкоторых потенциал зависит только от одной координаты. Примерами могут служить: плоский конденсатор, краевыми эффектами которого можно пренебречь, цилиндрический конденсатор, длина которого значительно превосходит его диаметр, сферический конденсатор.

86
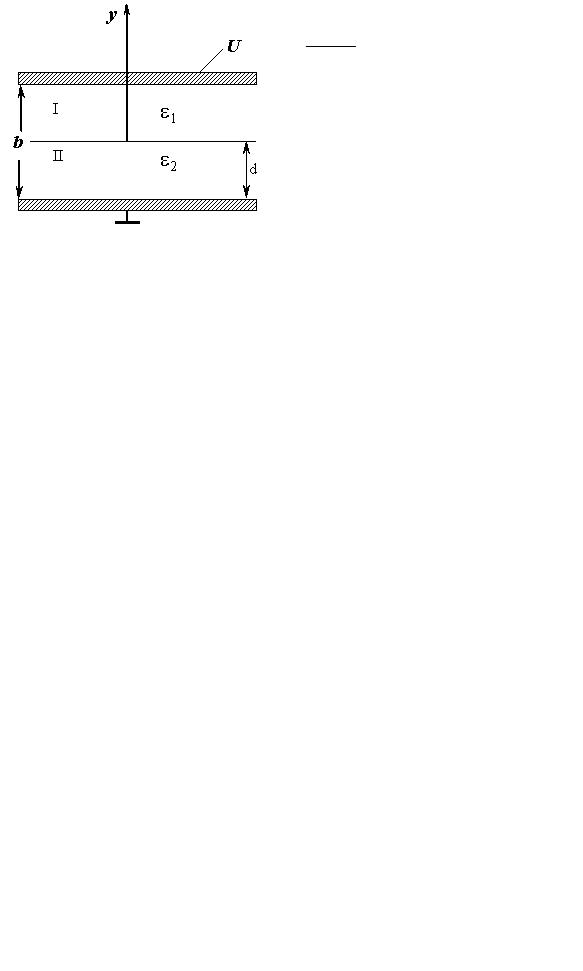
Задача №1.
Две плоские металлические пластины однородного диэлектрика толщиной d проницаемостью ε (конденсатор). На верхнюю пластину подан потенциал U , нижняя пластина заземлена (рис. 3.1). Найти: потенциал ϕ между пластинами, напряженность поля E , вектор электрического смещения D , заряд на одной из пластин конденсатора q , его емкость С. Линейные размеры пластин много больше размера d .
Решение:
Выбираем прямоугольную систему координат, в которой ось у перпендикулярна поверхности пластин. В этом случае, можно считать потенциал ϕ зависящим только от координаты у . Решение проводим с помощью уравнения Лапласа (3.5а) с применением граничных условий для потенциала на границе раздела диэлектрикметалл (3.9).
|
d 2 ϕ |
= 0 имеет общее решение |
ϕ = Ay + B |
, где |
|||
Уравнение Лапласа dy 2 |
|||||||
|
|||||||
A и B неизвестные постоянные подлежащие определению. Для их |
|||||||
определения используем граничные условия: а) при |
y = 0 ϕ = 0 ; б) |
||||||
при у = d ϕ = U . |
|
|
|
|
|
||
В результате получим |
B = 0 , A = |
U |
и выражение потенциала |
||||
|
|||||||
|
|
|
d |
|
|
||
ϕ = U y . d
Как следует из решения, потенциал линейно возрастает от 0 до U при изменении координаты y от 0 до d .
Напряженность поля и электрическую индукцию определяем
|
R |
R |
0 |
dϕ |
R |
0 |
U |
|
R |
R |
|
U |
|
|
|
|
|
|
|
|
|||||||||
как |
E = − gradϕ = − y |
|
= − y |
|
|
, |
D = y |
0ε |
|
.(*) |
||||
|
dy |
|
|
d |
d |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поверхностная плотность заряда определяется из выражений на верхней
пластине у = d ξ = ε dϕ = ε U ,
dn d
Рис. 3.2.

87
на нижней пластине у = d |
ξ = −ε |
dϕ |
= −D . |
|||||
|
|
|||||||
|
|
|
dn |
|||||
Заряд пластины конденсатора q = ξ S , |
||||||||
емкость конденсатора C = |
q |
= |
q |
= |
ε S |
. |
||
U1 − U 2 |
|
|
||||||
|
|
U d |
||||||
На рисунке 3.2 изображены: распределение электрических зарядов на поверхностях электродов и электрическое поле между пластинами.
Задача №2.
Сохраним условие задачи №1, но диэлектрическую проницаемость среды, заполняющей конденсатор, принимаем e = e0eαy .
Решение:
Для данной задачи потенциал зависит от у, поэтому уравнение
Лапласа |
divε gradϕ = 0 |
|
|
преобразуется |
|
к виду |
d |
(ε0eαy |
dϕ |
) = 0 и |
|||||||||||||
|
|
dy |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|||
|
|
|
|
|
|
|
|
α y |
|
dϕ |
|
|
|
|
|
|
|
|
|
|
|
||
удовлетворяется |
при |
|
ε0 ×e |
|
× |
|
|
= A |
, |
где |
А |
– |
неизвестная |
||||||||||
|
|
dy |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
постоянная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Потенциал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ϕ = ∫ |
|
|
e − α y dy |
= − |
|
|
|
e −α ó |
+ B . |
|
|
|
|
|
|
|
|
|
|
|
|||
ε |
0 |
ε |
0 |
α |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Неизвестные постоянные A и В могут быть определены из |
|||||||||||||||||||||||
граничных условий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1. при y = 0 ϕ = 0 , откуда |
B = + |
|
A |
|
|
ϕ = |
A |
(1 − e −αy ) . |
|||||||||||||||
ε α |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε α |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
||
2. при y = d ϕ = U
Следовательно, ϕ
откуда U = A
ε 0α
= U (1 − e − α y ) 1 − e − α d
(1 − e−αd ) A = |
Uε |
0α |
||
|
|
|
. |
|
(1 |
|
|
||
|
− e−αd ) |
|||
.
Напряженность электрического поля Ey = − |
dϕ |
= |
Uαe |
−αy |
, |
||||
|
|
|
|
||||||
dy |
1− e |
−αd |
|||||||
|
|
|
|
|
|||||
|
R |
R |
εUαe |
−α y |
|
|
|||
вектор электрического смещения |
D = ε E = − |
|
|
|
|
||||
|
|
1 − e−αd . |
|
|
|||||
88
Ёмкость конденсатора определяется с помощью известной формулы:
C = q .
U
Заряд при y = 0 равен q = D = S = ξS = ε USα
у 0 1 − e−αd
определяем
. Используя (3.18),
|
|
ε |
α S |
|
с = |
|
|
|
. |
1 - |
e − α d |
|||
Задача №3.
Сохраним формулу задачи №1, но добавим условие, что между пластинами в диэлектрике размещен заряд с объемной плотностью ρ .
Решение:
В этом случае необходимо использовать уравнение Пуассона (3.5), из которого путём интегрирования определяется
|
dϕ |
= −∫ |
ρ |
dy = − |
ρ |
y + A , |
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
|
dy |
|
|
|
ε |
|
ε |
|
|
|||||||
|
|
|
|
а затем потенциал ϕ = ∫ (− |
ρ y + A)dy = − ρy2 + Ay + B |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
2ε |
|
|
|
|
Граничные условия остаются такими же как в задаче № 1 В=0, |
||||||||||||
|
|
|
|
U + |
ρ |
d2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
A = |
|
|
|
|
2ε |
. |
|
|
|
|
|
|||||
|
|
|
d |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Окончательное выражение для |
потенциала имеет вид |
|||||||||||
ϕ = |
ρ |
|
|
|
|
|
|
|
U |
|
|
|||||
|
(d × y - y 2 ) + |
|
y , |
|
|
|||||||||||
2ε |
d |
|
|
|||||||||||||
из которого следует, что граничные условия удовлетворяются. Напряженность электрического
поля (3.4) EÓ |
= -[ |
ρ |
(d - 2 y) + |
U |
] имеет. |
|
2e |
|
|||||
|
|
|
|
d |
||
Можно |
построить |
|
график |
|||
зависимости ϕ( y) при заданном отрицательном и положительном объемном заряде.
Рис. 3.3
