Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Электромагнитные поля и волны.-5

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

3.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 288 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

2.3.Задачи для самостоятельного решения

1.Вектор E = E0 z0 cost sin x . Определить вектора B и H .

Ответ: B = y0 E0 cos x sin t ; H = Bm H = y0 Em0 cos x sin t .

2. Чему равен заряд в кубе с ребром a , если начало координат расположено на вершине куба, а ось совпадает с одним его ребром, вектор

D = x2 x0 ? 2

Рис. 2.11. К задаче №2

Ответ: q = a4 .

3. Какое физическое толкование может быть дано уравнению rot H = 10z0 ?

Ответ: Вихревое магнитное поле H возбуждено током, плотность которого 10 Ам и направление вдоль оси z .

4. Какие из представленных магнитных полей при μ = const

удовлетворяют уравнению Максвелла, т.е. могут быть реализованы?

1)H1 = x0 3x cos ωt − y0 3cos ωt ;

2)H2 = y0 cos x cos ωt − x0 sin y cos ωt ;

3)H3 = x0 6x cos ωt − y0 3y2 cos ωt .

Ответ: Второе поле.

При каких условиях выполняется равенство

div

= 0 ,

, H

= H × rot

× rot H .

где

– радиус-вектор? Справка: div

, H

Ответ: когда			= 0 .
		δ
6.	Заряд q = 10−3 Кл			со скоростью			ν = 100 м с под углом
ϕ = 60°	пересекает поле			E =10−2		В м.	Какова сила воздействия
					y
				0
поля E на заряд и зависит ли она от скорости и угла?

Ответ: F =10−5 y0 cos j Кл× В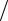м.

7. В сферическом объёме радиуса R равномерно распределён гармонически изменяющийся заряд с объёмной плотностью r = 1× cos wt . Чему будет равен ток проводимости, связанный с этим зарядом?


Ответ: Iпр =		4	pR3wsin wt .

	3
8.	В объёме V имеется заряд q = 2 Кл и заряд q2 . Определить
q2 , если известно,				что поток вектора		через		поверхность	S ,
					D
охватывающую объём V , равен 1 Кл.
Ответ: q2 = −1 Кл.
9.	Определить			циркуляцию вектора				по контуру	с
							B

координатами (0,0) ; (0,1) ; (1,1); (1,0) , если плотность тока

проводимости

пр =

смещения

j0 xy ,

j0 ^ XOY ; плотность тока

∂

= 0 ; μ = 3μ0 .

∂t

Ответ: 0,75μ0 .

10.

Сфера

радиуса a

имеет заряд с

объемной плотностью

r = r

r 2

× sin q. Найти полный заряд сферы

Q .

0 a2

Ответ: Q = rp2 a3 .

11.

В полом металлическом объеме,

заполненном

воздухом

(рис. 2.12), существует электромагнитное поле, представленное

векторами

0 H y , где проекции векторов

z0 E и H =

0 H x

имеют вид:

sin π x sin π y cos wt,

Ez = -Ey

H x

H y

=-H x0

=H y0

sin π x cos π y sin wt, a b

cos π y sin π x sin wt. b a

Рис. 2.12. К задаче №11

Найти поверхностный заряд на внутренних металлических стенках объема и токи, протекающие по его боковым стенкам. При каких значениях координат x и y компоненты напряженности магнитного поля H x и H y максимальны?

Ответ: ξ = Dz = ε0 Ez , jz = H x при y = 0 и b , jz = H y при x = 0

и a .

12. Напряжённость электрического поля изменяется по закону

	a
	a
Ex = E0 ×		, Ey = 0 ,			Ez = 0 . Требуется найти объёмный заряд ( a –
Ex = E0 ×	x	, Ey = 0 ,			Ez = 0 . Требуется найти объёмный заряд ( a –
постоянная).
Ответ: r= -e				× Е		а	.
Ответ: r= -e				× Е			.
			0		0	х2
13. В некоторой области с диэлектрической проницаемостью ε

задано поле

= k(

y2 ). Вычислить плотность объемного

заряда.

Ответ: ρ = 2κ( x + y) .

14. Задано поле вектора

при 0 £ r £ a,

D =

при a £ r

£ ¥,

где r – радиус-вектор. Найти распределение зарядов, образовавших такое поле.

Ответ: ρ = 3κ при 0 ≤ r ≤ a ; ρ = 0 при a ≤ r ≤ ∞ .

15. Напряженность поля в некоторой области меняется по

закону

= E

;

= 0 ;

= 0 ; x [a,b].

Найти объемную

a x

плотность заряда в данной области, если εa

= ε0 .

Ответ: ρ = −

ε E .

(0,0) ;

16. Определить циркуляцию векторов

по контуру

(0,1) ;

(1,1);

(1,0),

если объемная плотность тока проводимости

= 0

, а вектор электрической индукции

y sin xt

пр

Ответ: 0,5 × cos t .

сред ( x = 0 )

17. Вблизи границы раздела двух

задано

распределение вектора

1 = (5

0 ), x > 0;

0 + 5

2 = (4

0 + 3

0 ), x < 0.

Есть ли на границе раздела поверхностный заряд? Ответ: есть.

18. Электрическое поле, имеющее амплитуду напряженности

15 В м	и частоту 0, 6 ГГц, существует в среде с параметрами
ε = 3,6 ,	μ = 1, σ = 0, 72 См м. Определите амплитудное значение и

фазовый угол вектора плотности полного тока, существующего в каждой точке данной среды.

Ответ: δm = 10,8 А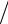м2 , ток опережает напряженность поля на угол 0,17 рад .

19. Определить ЭДС в замкнутом контуре, изображенном на рисунке в виде треугольника ABC , если известен вектор

H = Нm y0 sin ϖt .

Рис. 2.13. К задаче №19

Ответ: ЭДС = −ωμ Нm y0 cos ϖ t .

20. В однородном магнитном поле с напряженностью H вращается прямоугольная плоская рамка со скоростью ω = 2πf .

Стороны рамки a и b , число витков N , магнитная проницаемость среды ma = m0 , f – число оборотов в секунду. Вычислить ЭДС в рамке.

Ответ: Э = -2pnNm0 × H × a × b × sin 2pnt .

21. Вектор электрического смещения равен

D = xx0 + yy0 − (x + y)z0 .

	Найти объемную плотность заряда.
	Ответ: 2 Кл м3 .
	22. По рамке с размерами a × b , расположенной на расстоянии
r	от прямолинейного бесконечного			проводника, протекает	ток
I	= I0 cos ωt . Вычислить	величину		электродвижущей силы	в
проводе.
	Ответ: Э = ωμ0в I0 × l n	r + a	×sin wt .
	Ответ: Э = ωμ0в I0 × l n		×sin wt .
	2p	r
	23. В соленоиде без сердечника, содержащем N = 1000 витков,

при увеличении силы тока магнитный поток увеличился на 2 мВб.

Определить среднюю ЭДС самоиндукции, возникающую в соленоиде, если изменение силы тока произошло за 1 с.

Ответ: 2 В.

24.	Напряженность магнитного поля в среде, обладающей
μr = 102 ,
μr = 102 ,	H = 2 А м. Чему равен вектор намагниченности среды M
?

Ответ: M = 0, 25 ×10−3 Тл.

25. При каких условиях выполняется равенство div r , H = 0 ,

где r – радиус-вектор, H – вектор напряженности магнитного поля.

= 0 .

Ответ: div H

26. Вычислить и определить направление вектора

в среде с

проводимостью,

равной

нулю,

если

0 H0 cos(tw - kz ), где

k = const , ω = const .

= -

0 kH0

Ответ:

cos(wt - kz) .

27. Удельная проводимость среды σ выражается тензором.

σ ,

0 + d1 , где

0 = s ×

Какой

вид

имеет

этот

если

= c ×

× H

κ –

постоянная.

kH0

Ответ: s =

28. Под каким углом расположены векторы

, если

e =

аE = x0 E .

Ответ: 90° .

29.Вдоль тонкостенной трубы радиуса a и тонкого

проводника, совпадающего с осью трубы, протекают постоянные токи I2 и −I1 от оси трубы на расстояниях a2 и 3a .

Рис. 2.14

Каково магнитное поле в точках, от

Ответ: H = I2 − I1 ; H = 0 .

1 6p× a 2

30. В поле E = 3 × E0 × x × i + 2 × E0 × y × j - E0 × k перемещается единичный заряд из точки A(0,1,0) в точку B(0,5,0). Определить совершаемую при этом работу.

Ответ: 24 × E0 .

31. Как изменится токи проводимости ( δпр ) и смешения ( dсм );

если при тех же E и H , ε и σ среды увеличатся вдвое?

ηY

Рис. 2.15

Ответ: dсм и δпр – удвоятся.

32. По идеально проводящей плоскости протекает постоянный ток, причем поверхностная плотность тока h Ам в каждой точке вблизи плоскости. Определить магнитное поле в любой точке вблизи плоскости.

= -h×

Ответ: H

0 А м.

33. Вектор

направлен под углом 30° к границе раздела двух

сред,

диэлектрические

проницаемости

которых равны

e1 = 1,

. Определить угол α1 между

и границей раздела.

Ответ: α2 = 45°.

23. В некоторой точке пространства вектор напряженности

поля

= 20

0 В м,

электрического

то

время как

вектор

=10

+ 30

А м2 .

Пойнтинга

Определить

вектор

напряженности магнитного поля.

Ответ: −1,5

x0 + 0,5

А м.

34. Ток возникает в среде за счет движения объёмного заряда

= 5xx0 .

со

скоростью

Как

зависит

от

координат объёмная

плотность заряда ρ ? Считать плотность тока постоянной; другие типы токов отсутствуют.

Ответ: ρ = c . x

35. Вблизи металлической поверхности задано распределение вектора D : D = 5x0 + 53y0 . Полагая, что поле в металле отсутствует, определить поверхностную плотность заряда на поверхности металла.

30o

металл

Рис. 2.16

Ответ: ζ = 10 .

36. Диэлектрик коаксиального кабеля имеет удельную проводимость σ. Определить напряженность электрического поля E внутри кабеля, если ток утечки на единицу длины равен I .

Ответ: E = r0

2π ×

σ × r

37. На границе (плоскость XZ) раздела двух сред векторы

1 и

)×ε

имеют вид

= ( 2

+ 5

+ 4

) × ε

;

=(4

Определить напряженности электрического поля в этих средах. С какими средами, с точки зрения материальных уравнений, мы имеем здесь дело?

= (2

0 +5

0 +4

0 )

= (4

0 +5

0 +8

0 ).

Ответ: E1

Обе

среды

анизотропные.

38. Найти поток вектора плотности полного тока

δ пол =x0 5+ y07+z08 через поверхность куба со стороной а=5 m. </q>

Ответ: 0.

39. Имеются 2 полубесконечных cреды: изотропная (1-ая) и анизотропная (2-ая). В 1-ой среде плотность тока проводимости

								77
		1 =			O		и проводимость σ1 = σ, во второй среде проводимость
	j					j
	j		x			j
				ασ			βσ	0
				ασ			βσ	0
σ 2 =				βσ			ασ	0
				0			0	σ

1	2
1
		Z

Рис. 2.17

Записать выражение вектора j2 во 2-ой среде.

			R	R
Ответ: j2
		= j1 (α xo		+ β yo )
40. Найти поток вектора плотности полного тока jполн через
поверхность куба со стороной a . П j = ∫					R	R
					jполн ds = ∫ div jполн dv .
				S		V
Ответ: П = jполн = 0 .
41. Если вектор				R
				H направлен всюду параллельно оси OX, то
как расположены линии полного тока?
Ответ: в плоскости YOZ.
42. Как изменятся токи проводимости jпр и смещения jсм, если
	R		R
при тех же E		и H параметры среды ε и σ учетверить?

Ответы: jсм=4jсмo; jпр=5δjпрo.

43. В любой точке объёма V, где существуют только токи

проводимости и	токи смещения Е=-grad		φ(x,y,z,t).	Что можно
сказать о векторе	R	в наиболее общем случае?
сказать о векторе	H	в наиболее общем случае?
R
Ответ: H -экспоненциально убывает во времени.
44. Внутри		полой металлической трубы радиуса a
(цилиндрическая		система координат –	r, α,z)	возбуждено

переменное электрическое поле. Запишите граничные условия для магнитного поля на стенках (r =a), считая поле в металле равным нулю (η-плотность поверхностного тока).

Ответ: Br = 0, H α = −η z , H z = η α

45.Вычислить div[r, E], где Е-вектор напряженности

электрического поля, независимый от времени, а r-радиус-вектор точки. Какой из ответов наиболее полон и точен? Ответ: 0

46. В некотором объеме свободного пространства имеется

электрическое поле

= 10

и магнитное поле

= 15

. Заряд

q = 1×10−9 Kл

впрыскивается в этот объем со скоростью

=1 ×10

Определить силу,

действующую

на

заряд и

ее напряжение.

μ0 = 4π ×10−7 Гн

Ответ:

28,84 ×10−9

47. Металлический шар радиусом а помещен в поле Е0

заданное

уравнением

ϕ (r ) = E0 (a3

2 - r )cosθ .

Определить

поверхностную плотность заряда ζ

∂ϕ = En .

на шаре, если

¶n

Ответ: ζ = 3 ×ε × E0 cosθ .

48.

Вектор

электромагнитного

поля

равен

E = E 0 x0 sin(wt - wem × z) .

Определить вектор H .

Ответ: H = e mE0 y0 sin(wt - wem × z) .

49. По двум параллельным проводам, отстоящим один от другого на расстоянии L протекают постоянные однонаправленные токи I1 и I2 . На каком расстоянии r от первого провода, на линии их соединяющей, расположена точка, на которой магнитное поле

равно нулю? Ответ: r = L × I1

(I 2 + I1 )

50. Чему

равен

и как направлен

вектор плотности тока

σ 1

σ 2

проводимости δ пр jпр ,

если E = x0 E , в σ =

σ 1

σ 0

σ 2

σ 0

Ответ: δ пр

= σ 1 E y0

+ σ 2 E z0 .

<<< < Предыдущая 1 2 3 4 5 6 78 / 288 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023196.13 Кб3Электромагнитная экология..pdf
#
05.02.2023652.23 Кб18Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб14Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб46Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб19Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб38Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб41Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб50Электромагнитные поля и волны..pdf
#
05.02.20233.12 Mб26Электроника 1. Физические основы электроники-1.pdf
#
05.02.20231.01 Mб10Электроника 1. Физические основы электроники.pdf
#
05.02.2023688.65 Кб7Электроника 2. Электронные приборы.pdf