Электромагнитные поля и волны.-5

49

2.1.2. Граничные условия

Граничные условия непосредственно следуют из уравнений Максвелла и определяют поведение векторов поля на границе раздела двух сред.

Каждый произвольно ориентированный вектор вблизи граничной поверхности может быть представлен в виде сумм нормальной и тангенциальной составляющих:

A = n0 An + τ0 Aτ ,

где τ0 – касательный к граничной поверхности единичный вектор; n0 – нормаль к поверхности. Поэтому граничные условия формулируются для тангенциальных и нормальных компонент поля.

Граница может проходить между двумя диэлектриками (граница д-д) и между диэлектриком и металлом (граница д-м). Ниже приведены граничные условия для этого вида границ.

Граничные условия для нормальных компонент электрического поля на границе диэлектрик-диэлектрик:

∙D1n = D2n – при отсутствии поверхностного заряда ξ S на

проницаемости первой и второй среды соответственно. Граничные условия для нормальных компонент магнитного

поля на границе диэлектрик-диэлектрик:

проницаемости первой и второй среды соответственно.

50

Граничные условия для тангенциальных компонент электрического поля на границе диэлектрик-диэлектрик:

проницаемости первой и второй среды соответственно;

∙E1τ = E2τ .

Граничные условия для тангенциальных компонент магнитного поля на границе диэлектрик-диэлектрик:

проницаемости первой и второй среды соответственно;

∙H1τ = H2τ – при отсутствии поверхностного тока jS на

условий.

Граничные условия для компонент электрического и магнитного полей на границе диэлектрик-металл:

∙Dn = ξS , где ξ S – поверхностный заряд на границе раздела;

∙Eτ = 0;

∙B1n = 0 ;

∙Hτ = jS , где jS – поверхностный ток на границе раздела

диэлектрик-металл.

2.2. Примеры решения задач

2.2.1. Задача №1

Доказать, что линии полного тока непрерывны и замкнуты.

Решение:

Какое равенство должно иметь место, чтобы линии полного

тока jполн были замкнуты? div jполн = 0 и С∫ jполнdS = 0 – эти

S

равенства нам и нужно доказать.

51

Запишем уравнение Максвелла, в которое входит плотность полного тока jполн . Из закона полного тока (первое уравнение Максвелла) следует, что rot H = jполн . Возьмем div от обеих частей этого равенства:

div rot H = div jполн.

выходит). Следовательно, линии полного тока непрерывны и замкнуты.

2.2.2 Задача №2

Используя уравнения Максвелла, вывести уравнения непрерывности и закон сохранения заряда.

Решение:

Закон сохранения заряда утверждает, что всякому изменению заряда в некотором объёме соответствует электрический ток, втекающий в объём или вытекающий из него. Он является следствием закона непрерывности полного тока.

Запишем первое уравнение Максвелла в дифференциальной

возьмем дивергенцию от всех слагаемых этого равенства:

52

или

После интегрирования по объёму

r = 1× cos wt . Чему будет равен ток проводимости, связанный с этим зарядом?

Решение:

Используя закон сохранения заряда

Iпр = − dq , dt

Продифференцировав объемную плотность заряда ρ по времени и учитывая, что объем сферы равен 43πR3 , получим:

Iпр = 4 πR3ωsin ωt. 3

2.2.4. Задача №4

Может ли вектор B = x0 5x + y0 y быть вектором магнитной индукции?

Решение:

53

Заданный вектор может быть вектором магнитной индукции только в том случае, если он будет удовлетворять четвертому уравнению Максвелла. Так как

div B = ¶Bx + ∂By = 5 +1 = 6 ¹ 0,

¶x ¶y

то заданный вектор не может быть вектором магнитной индукции.

2.2.5. Задача №5

Положительный заряд с объёмной плотностью ρ = 10−3 Клм3

равномерно распределён в сферическом объёме радиуса R = 1 см

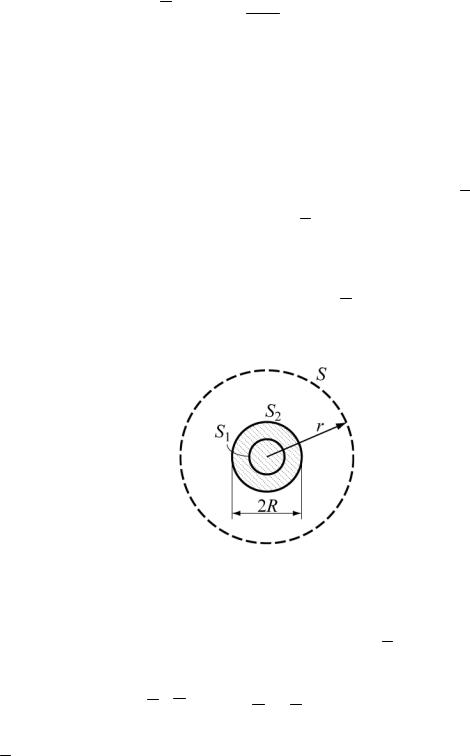
(рис. 2.1). Найти вектор электрического смещения D и вектор напряженности электрического поля E в областях:

1.0 ≤ r ≤ R ;

2.R ≤ r ≤ ∞ .

Построить график зависимости D (r ). Дать численный результат при: r1 = 0, 2 см, r2 = 1 м.

Рис. 2.1. К задаче №5

Решение:

Исходной формулой для решения этой задачи является третье уравнение Максвелла. Так как вектор D распределен по поверхности равномерно, то

С∫ DdS = С∫ Dr r0 dSr0 = Dr S = q,

S

где r0 – единичный радиус-вектор.

Следовательно:

1. Для первой области ( 0 ≤ r ≤ R ) при S = 4πr 2 получим:

54

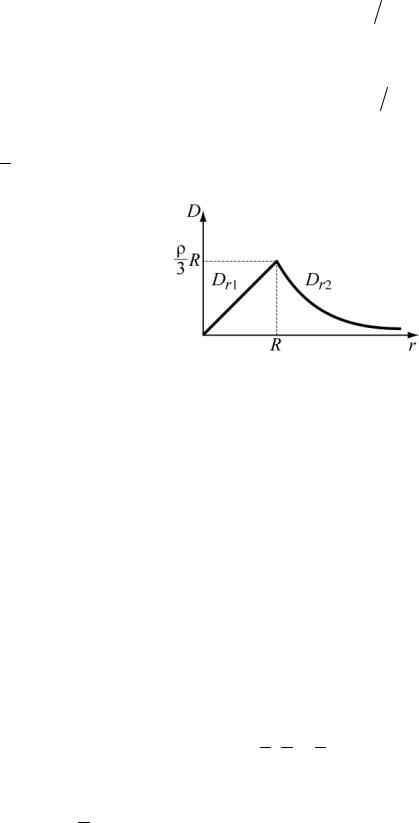
D (r ), показанный на рис. 2.2.

Рис. 2.2. К задаче №5

2.2.6. Задача №6

По прямолинейному круглому проводнику протекает ток силою I . Найти выражения, определяющие напряженность магнитного поля внутри проводника (область 1 – 0 ≤ r ≤ R) и вне

r2 = 1 м.

Решение:

Для решения этой задачи используется первое уравнение Максвелла в интегральной форме

С∫ Hdl = Iполн.

L

Формулировка этого закона утверждает, что циркуляция вектора H по контуру L определяется величиной полного тока, охватываемого этим замкнутым контуром (рис. 2.3).

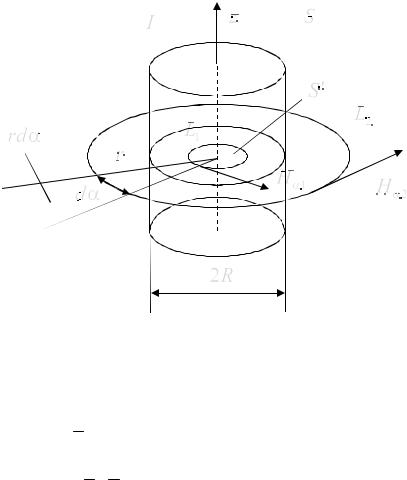
55

Рис. 2.3. К задаче №6

Так как элемент длины контура в цилиндрической системе координат равен d l α = α0rdα , то

2π

С∫ Hd l = ∫ Hα × rda = Hα × 2pr = I.

График зависимости H (r ) представлен на рис. 2.4.

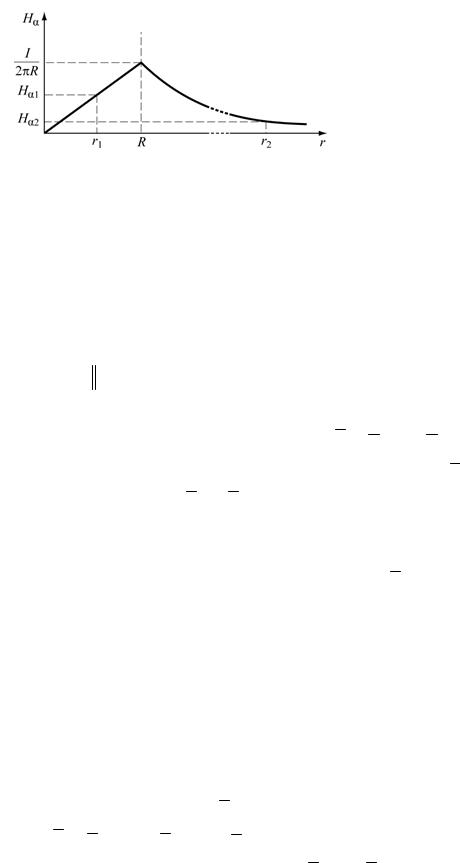
56

Рис. 2.4. К задаче №6

Результат численного расчёта: Hα1 = 0,16 Ам, Hα 2 = 15,9 Ам.

2.2.7. Задача №7

Анизотропный диэлектрик имеет диэлектрическую проницаемость

К нему приложено электрическое поле E = x0 Ex + z0 Ez .

Найдите выражение для вектора электрического смещения D . Определите угол между векторами E и D .

Решение:

Так как диэлектрик имеет анизотропную диэлектрическую

проницаемость, то вектор электрического смещения D будет определен следующим выражением:

Перемножая строку на столбец, смещения:

DX = ε1EX , DY = αEX , DZ = ε0 EZ .

Из них составим вектор смещения D

D = x0ε1Ex + y0αEx + z0ε0 Ez .

Для определения угла между векторами D и E запишем скалярное произведение векторов

выражение для вектора магнитного поля H :

H= Bm H = z0 2mEw0 sin wt.

2.2.10.Задача №10

В некотором объеме свободного пространства имеется электрическое поле E =10 y0 Вм и магнитное поле H =15x0 Ам.

Заряд q = 10−9 K влетает в этот объем со скоростью u =106 z0 Ам.

Найти силу, действующую на заряд и её направление.

Решение:

На заряд, находящийся в магнитном и электрическом поле действует сила:

F= q{E + υ × B }.

Сила электрического поля, воздействующая на заряд равна:

FЭ = qE =10−9 ×10 × y0 =10 ×10−9 y0 .

Сила магнитного поля, воздействующая на заряд равна при

В = m0 Н ( m0 = 4p×10−7 Гнм ), определяется как векторное произведение скорости движения заряда и вектора магнитной индукции:

Суммарное воздействие сил электрического и магнитного полей направлено по оси y0 и равно по величине

F = Fэ + Fм = 28.84 ×10−9 H.