Электромагнитные поля и волны.-5

39

Ответ: 0.

9. Найти градиент скалярной функции r , определяющей расстояние между текущей точкой М ( x, y, z ) и постоянной точкой

A(a,b, c) .

Ответ: G = grad r = r0 , r = r0 × r .

10. Найти grad скалярного поля U ( x, y) = 3x2 × y - 3x × y3 + y4 в

точке M (1, 2) .

Ответ: 3х2 у + 3ху3 + у4 .

11. Найти уравнение векторных линий

E = E0 sin θ θ0 + E0 cos θα0 .

12. Вывести уравнение векторной линии поля A = x0 (- y) + y0 x .

– радиус-вектор.

Ответ xdx + ydy = 0 , x2 + y2 = c2 .

16.Определить поток радиус-вектора через поверхность

единичного куба. Ответ: Π = 3 .

17.Найти поток вектора r – радиус-вектора.

Ответ: 2 j .

18. Определить уравнения векторных линий поля E = grad ϕ ,

где j = j(r ), r = x2 + y2 .

20. Сколько из приведенных ниже формул являются ложными?

1) rot grad ϕ = 0 ;

Ответ: 3.

21. Сколько из приведенных ниже соотношений ошибочны? 1) С∫ Hdl = ∫ rot H dl ;

LS

2)∫div rot B dV = 0 ;

V

3) С∫ DdS = ∫div D dV ;

S V

4) ∫ rot grad jdV = 0 ;

S

5) С∫ rot H dS .

S

Ответ: 3.

22. Вычислить циркуляцию вектора A = 5i + 7 j по контуру L .

Рис. 1.18. К задаче №22

24. Сколько из приведенных полей являются потенциальными?

1)C = z × j ;

2)A = r - y × i ;

3)B = y2 k + z2 j ;

4)D = x × j - 4 × k .

Ответ: Ни одно поле не потенциально.

25. Найти циркуляцию вектора

A = ( x − 2z ) i + ( x + 3y − z ) j + (5x + y)k

по контуру треугольника ABC в направлении, указанном на рисунке (по теореме Стокса).

42

Ответ: div A = 0 .

29. Сколько из приведенных полей являются потенциальными полями?

1)A = 5xi ;

2)B = 8x2 i + zyk ;

3)D = y2 j + z2 k ;

4)C = zz .

Ответ: 2.

30. Вычислить ротор вектора D = zj + zk .

Ответ: rot D = −i .

31.Найти наибольшую скорость изменения поля

ϕ= 5x2 yz − 7xy2 z + 5xyz2

вточке М (1,1,1).

Рис. 1.20. К задаче №34

43

Ответ: Ц = − 1 m .

2

показанному на рисунке?

Рис. 1.21. К задаче №38

Ответ: −45 .

39. Вычислить div grad ϕ , где ϕ = x2 + y2 + z2 . Ответ: 6 .

40. Сколько из приведенных полей являются соленоидальными полями?

1)A = 2zj ;

2)B = rot M ;

3)C = k , r ;

4)D = zk .

Ответ: 3.

41. Вычислить циркуляцию вектора A = 4 j + 8k по контуру L .

44

Рис. 1.22. К задаче №41

Ответ: Ц = 0 .

42. Определить дивергенцию вектора

B= (r , k )kz + i , j , r .

Рис. 1.23. К задаче №43

Ответ: 0 .

44. Как изменится поток радиус-вектора r через поверхность куба с центром в начале координат, если все ребра куба увеличить в два раза?

Ответ: 3a2 .

контуру, показанному на рисунке, радиус окружности R = 1 / 2 .

45

Рис. 1.24. К задаче №46

Ответ: Ц = π .

2

47. Определить величину потока вектора b = (4z + 4x3 )k через квадратную площадку со стороной 1 м , лежащую в плоскости z = 3 м как показано на рисунке.

e = i + j 3 .

Ответ: −4 .

46

Глава 2. Уравнения Максвелла

Целью данного занятия является закрепление теоретического материала путем решения задач по следующим вопросам курса:

∙уравнения Максвелла в интегральной и дифференциальной формах;

∙материальные уравнения;

∙граничные условия.

В начале каждой части занятия приводятся краткие теоретические сведения; в конце занятия – задачи для самостоятельного решения с ответами.

2.1. Краткие теоретические сведения

Электромагнитное поле представляет совокупность полей электрического (векторы E , D ) и магнитного (векторы H , B ), находящихся во взаимной зависимости. Вектор E – напряженность электрического поля, измеряемая в вольтах на метр ( В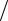м); вектор

D – электрическая индукция – кулон на квадратный метр ( Клм2 );

вектор H – напряженность магнитного поля – ампер на метр ( Ам

); вектор B – магнитная индукция – в веберах на квадратный метр ( Вбм2 ).

В компактной форме операций векторного анализа запишем уравнения Максвелла, которые заключают в себе основы теории электромагнетизма.

Уравнения Максвелла в интегральной форме: 1. Закон полного тока

47

Переход от уравнений Максвелла в интегральной форме к уравнениям в дифференциальной форме осуществляется с помощью теорем Остроградского – Гаусса (1.24) и Стокса (1.29).

Уравнения Максвелла в дифференциальной форме:

Плотность полного тока представляет сумму четырех токов:

соответственно плотности тока смещения, плотности тока проводимости, плотности тока переноса и плотности стороннего тока.

Выражения каждого из токов приведены в таблице:

Вэти выражения входит σ – удельная объемная проводимость вещества.

Вкаждой конкретной задаче присутствует один или несколько токов, соответствующих условиям задачи.

48

2.1.1. Материальные уравнения

Связь векторов электромагнитного поля в некоторой материальной среде представляется материальными уравнениями:

восприимчивость и χМ = μr −1 – магнитная восприимчивость среды; e0 =10−3 36p » 8,856 ×10−12 Фм – электрическая постоянная

однородные и неоднородные, линейные и нелинейные, изотропные и анизотропные.

Неоднородными являются среды, в которых параметры μ , ε и

σявляются функциями координат. Нелинейными являются среды,

вкоторых параметры μ , ε и σ являются функциями самих полей.

Анизотропные среды отличаются от изотропных тем, что они в разных направлениях обнаруживают различные свойства. Для таких сред μ , ε и σ могут быть представлены виде тензора. Тензор представляет матрицу, состоящую из 9 независимых элементов. Материальные уравнения в этом случае приобретают вид: