Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Электромагнитные поля и волны.-5

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

3.52 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2821 22 23 24 25 26 27 28 > Следующая >>>

199

присутствует изменение формы поперечного сечения и изменение заполняющей среды (элементы - детали волноводного тракта).

В волноводах могут при определенных условиях распространяться волны электрического типа (тип − Е) , у которых компонентыH z = 0 , а Ez ¹ 0 (направление оси z совпадает с продольной осью волновода), и волны магнитного типа(тип − Н) , у

которых Ez = 0 , а H z ¹ 0 .

Из уравнений Максвелла получают инвариантные (справедливые для любой системы координат) соотношения, позволяющие определять поперечные составляющие векторов полей через продольные для любого типа волны и любого волновода:

× grad H z ] ,

(7.1)

E = -iβ × grad

Ez + iωμ ×[z

× grad Ez ] ,

(7.2)

H = -iβ × grad H z - iωε[z

∂

где

E = x EX + y Ey ,

H = x H X

+ y H y

-для

grad

= dx

+ y

¶x

¶y

прямоугольного волновода;

R 1 ¶

E = r

+α

Eα , H

= r

Hr +α

Hα и grad = r0

+α0

-для случая

¶r

¶α

круглого волновода;

γ 2

= (ξ )2

+ (η )2 =

2π

поперечное

волновое

число,

аналогично

λкр

(ξ ), (η ) - волновые числа вдоль одной поперечной координаты .

Основные параметры волн в волноводах следующие

β =

2π

- постоянная распространения волны в волноводе;

(7.3) k = 2π ε r μr

λ0

- волновое число в среде, заполняющей

волновод; (7.4)

		1		λ		0	2
Kd =	1 -						коэффициент дисперсии,	(7.5)
		ε		λ

			r		êð

гдеλ0 - длина волны в свободном пространстве;

λкр - критическая длина волны, определяется размерами и формой поперечного сечения волновода, а также типом волны Emn ,

200

H mn . Например, для прямоугольного волновода критическая длина волны равна

λкр =			2

	m		2	n 2
	m		2	n 2
				+
				+
		a		b .	(7.6)

Основным (низшим) типом волны считается тот, у которого наибольшая критическая длина волны - λ кр ,

Основной тип волны в волноводе распространяется при условии

λкр низший тип F λкр

высшиго типа ,

(7.7)

Таблица 7.1. Параметры волны в любом волноводе:

Длина

Фазовая

Групповая

Характеристичес

волны

скорость

кое сопротивление

волноводе

λ =

λ0

V =

c ×

(7.11)

εr

εr Kd

ãð

εr

(7.8)

(7.9)

( 7.10)

ZE = W0 × Kd

где с- скорость света

(7.12)

W =

μ0

= 120π

ε0

(7.13)

Средняя мощность, переносимая волной любого типа в любом волноводе, определяется интегрированием вектора Пойнтинга по поперечному сечению волновода

		1		R		R R.
		1	∫	R		&
P	=			Re{z	0	×[E × H * ]}dS
		2			0

ñð
			S			.		(7.14)
Коэффициент	ослабления					волны	α равен	сумме
коэффициентов ослабления в						металлических	стенках	α ì и

диэлектрике, заполняющем волновод αä , т.е. α = α ì + αä . Потери в металле определяются в общем виде выражением

201

× ∫

αm =

Hτ

. .

R R

∫ Re[E× H * ]dS

(7.15)

где Rs =

ωμa

- поверхностное

сопротивление металла,

2σ

H τ -

составляющая магнитного поля, тангенциальная к поверхности стенок волновода.

Потери в диэлектрике определяются с помощью выражения

ä =

π ×ε × tg Dε

λ × 1 -

(7.16)

êð .

После получения из уравнений Гельмгольца выражений продольных компонент конкретного типа волны и подстановки в уравнения (7.1) и (7.2), удовлетворения граничным условиям (нуль тангенциальных составляющих вектора электрического поля на стенках), получают выражения для всех составляющих векторов напряженностей электрического и магнитного полей.

7.1.1. Волноводы прямоугольного сечения

Волны типа Emn

β π m

π m x

π n y

E x

= -i

× E 0

× co s

× sin

e − i β z

β π n

π m x

π n y − i β z

E ó

= -i

× E 0

× sin

× co s

(7.17)

π m x

π n y

E z

= E 0

× s i n

e − i β z

π m

π mx

π ny

H x = iωε

× E0 × sin

× cos

e− iβ z

π m

π mx

π ny

H y = -iωε

× E0 × cos

×sin

e−iβ z

H z = 0 .

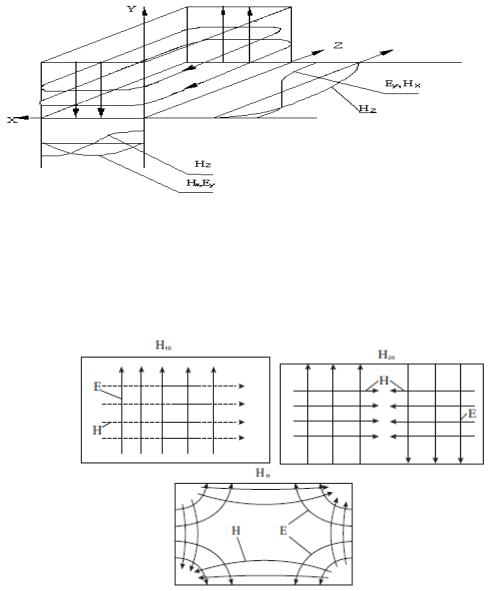
Низшей волной

электрического

типа

прямоугольном

волноводе является волна Е11 , картина поля которой изображена на рис. 7.3

202

Рис.7.3. Картина распределения полей в волноводе на волне типа E11

Волны типа H mn

π m

π mx

π ny

E x = iωμ

× H

0 ×cos

×sin

e−iβ z

π m

π mx

π ny

E y = -iωμ

× H0 ×sin

×cos

e−iβ z

= 0

βπ m

E z

π ny −iβ z

π mx

H x = i

× H0

×sin

×cos

(7.18)

βπ m

π mx

π ny −iβ z

H y = i

× H0

×cos

×sin

π mx

π ny −iβ z

H z

= H0

cos

×cos

π × m 2

π × n 2

2π

где γ =

(

)

- поперечное волновое число; (7.19)

λкр

m, n –

целые положительные числа;

a, b поперечные размеры широкой и узкой стенок волновода

соответственно;

критическая длина волны прямоугольного волновода λкр

равна

(7.6);

203

E0 , H 0 - амплитуды волны, определяются передаваемой

мощностью.
Основной волной в прямоугольном волноводе при		a > b
является волна Н10 (рис. 7.4),	ее критическая длина	волны
максимальна, и согласно (7.19), равна
λкрН	= 2a	(7.20)
10		(7.20)
10

Рис.7.4. Структура поля волны типа Н10 в прямоугольном волноводе.

Ближайшими высшими типами являются волны картина силовых линий которых приведена на рис. 7.5

Н20 , Н01, Н11,


		Рис.7.5.Картина векторных линий высших типов волн
Н	20	, Н , Н		в поперечном сечении.
	20	01	11

204

Передача энергии осуществляется всегда на основном типе волны, пока выполняется условие (7.7), другие типы волн в волноводе не возбуждаются.

Средняя мощность (7.14), переносимая волнойН10 в

прямоугольном волноводе определяется из соотношения

	=	abE	2
PсрH 10			0
PсрH 10		4 Z H		(7.21)
		4 Z H

Для волны Н10 коэффициент затухания в прямоугольном медном волноводе рассчитывается по формуле

λ 2 2b

εr

Í ï

αm =

λ 2

εr

W0 ×b ×

λ 2

0,104 × ε r

äá

];..èëè..αm =

]

λ ×

εr

b ×

. (7.22)

7.1.2. Волноводы круглого сечения

Для волноводов круглого сечения (рис. 7.2), работающих на волнах типа H mn , критическая длина волны равна

λ =	2π a
λ =	μ mn
кр	μ mn	(7.23)
кр

где μmn - n корень производной функции Бесселя Jm / (z) = 0 , а –

радиус волновода. Для волн типа			Emn критическая длина волны
равна		2 π a
λ =
		ν	mn
	кр			(7.24)

где vmn − n – й корень функции Бесселя Jm (z) = 0 . Значение корней

μmn и ν mn приведены в таблице 7.2.
Критическая длина волныλкр		в круглом	волноводе
максимальная у волны типа Н11
λ крH 11 = 3.41a		,	(7.25)

а ближайшим к ней типом волны является Е01, для которого
λ крE 01 = 2 .61 a		.	(7.26)
Таблица 7.2. Значения корней ν mn
	функции Бесселя J m ( z)

205

m	n

	1	2	3	4
	1	2	3	4

0	2,405	5,520	8,654	11,7
0	2,405	5,520	8,654	92
				92

1	3,832	7,016	10,173	13,3
1	3,832	7,016	10,173	24
				24

2	5,136	8,417	11,620	14,7
2	5,136	8,417	11,620	96
				96

3	6,380	9,761	13,015	16,2
3	6,380	9,761	13,015	23
				23

Значения корней μmn производных функции Бесселя J m / (x)

m	n

	1	2	3
	1	2	3

0	3,832	7,016	10,174

1	1,841	5,331	8,536

2	3,054	6,705	9,965

3	4,200	8,017	1,.403

Выражения для составляющих векторов поля в круглом волноводе имеют вид

волны типа

Волны типа

Нmn

ωμ

(γ

r) ×sin(mϕ )e−iβ z

E r = i

m × H

× J

2 r

ωμ × H0

× J / m (γ r) ×cos(mϕ )e−iβ z

Eϕ = i

(7.27)

= 0

E z

× J / m (γ r) ×cos(mϕ )e−iβ z

H r = -i

× H0

β m

(γ

r) ×sin(mϕ )e−iβ z

H ϕ = i

× H

× J

2 r

= H0 × Jm (γ r) ×cos(mϕ)e−iβ z

H z

Emn

(γ

r) ×cos(mϕ )e−iβ z

E r = -i

× E

× J /

(7.28)

206

β m

(γ

r) ×sin(mϕ )e−iβ z

Eϕ = i

× E

× J

2 r

= E

× J

(γ

r) ×cos(mϕ)e−iβ z

E z

H r

= -i ωε

× m × E × J (γ r) ×sin(mϕ )e−iβ z

H ϕ

2 r

= -i ωε × E0 × J / m ×(γ r) ×cos(mϕ )e−iβ z

= 0

Нz

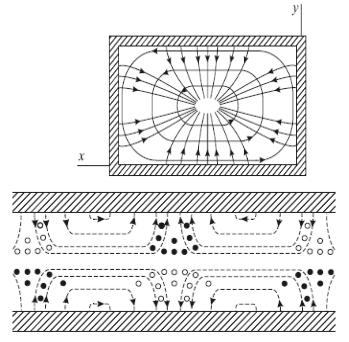
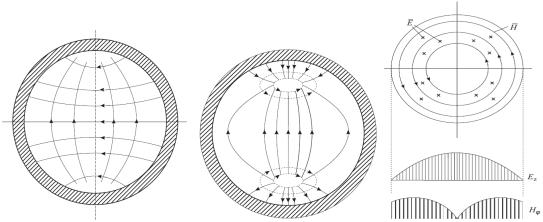
Картины силовых линий некоторых типов волн в поперечном

сечении приведены на рис. 7.6

Средняя мощность (7.14),

переносимая волной

Н11 в круглом

волноводе

π a

2 E 2

PñðH 1 1

4, 2 8 × Z H ,

(7.29)

в (6.29) величина Е0 -

максимальная амплитуда напряженности

электрического поля для волныН11.

а) б) в)

Рис.7.6. Структура полей в цилиндрическом волноводе волн типов:

а) Н11 , б) Е11 , в) Е01 .

Мощность, переносимая волной Е01 в круглом волноводе,

определяется [2]


P	=	π × E 20 × β012		× a4 × J1 (ν	01 )2		Ð =	0, 778 × E	2πωεβ
P	=						Ð =	0
ñðE01		2	× ZE ×ν 012			или	cpE01	q	(7.30)

207

Из соотношений (7.29), (7.30) находится амплитуда E0

электрического поля соответствующего типа волны. Например, для волны Е01 она равна

2P × Z

×ν

E0 E01

ñð

π × β012 × a4 × J1

(ν 01 )2

(7.31)

Средняя мощность,

переносимая

волной

Н01

определяется

соотношением

H 2π a

2 Z

cpH 01

ê ð

(7.32)

Постоянные затухания (

нп

) для волн в круглом волноводе [2]

имеют вид

λ â

α ìÅ 0 1 =

R S

W 0

(7.33а)

11 =

a W

1.8412

êð

(7.33б)

m 2

m n

a W0

λ μ m n

- m

λê ð

(7.33в)

Электрические поля любого типа волн в волноводах можно использовать для нагрева, сушки или сублимации диэлектриков, имеющих конечную удельную проводимость σ . Для этого следует поместить тонкий слой диэлектрика, чтобы не изменилось первоначальное поле, в электрическое поле волны волновода и определить мощность тепловых потерь РТ в нем.

P =ωε ×tgD×

∫

PÒ = ∫ σ ×

[Â ò

] или Ò

(7.34)

V ä

Vä

где, например, для цилиндрического волновода

E r2 + E α2

+ E z2

а для прямоугольного

E x2

+ E y2 + E z2

Мощность тепловых потерь расходуется на нагрев диэлектрика. Процесс сопровождается повышением температуры диэлектрика и возгонкой влаги. Чтобы нагреть образец весом m кг на T градусов (от Тн - начальной до Тк - конечной температуры,

208

т.е.	T = Тк − Тн ) при	его	удельной		теплоемкости	γ	Äæ	,
т.е.	T = Тк − Тн ) при	его	удельной		теплоемкости	γ		,
						êã× Ê
необходимо затратить [6] энергии
	W = 4.1868 × m ×γ × DT				[ Дж] .	(7.35)
Тепловая энергия		связана	с	СВЧ	мощностью и	временем
t = tk	− tí нагрева выражением
		P =	W	[Âò ]
		P =		[Âò ]
		Ò	t			(7.36а)
			t			(7.36а)

Подставляя (7.36) в (7.36а), получаем соотношение, связывающее параметры диэлектрика с величиной мощности, требующейся для его нагрева

		P =		4.1868×m×γ ×DT		[Вт]
		P =				[Вт]
		Т			t					(7.36б)
					t					(7.36б)
Можно определить из (6.36,б) температуру или время
разогрева, если что-то одно будет известно.
DT =	PÒ		Dt [0		Ñ ],Kèëè Kt	=	4.1868 × m ×γ × DT	[ñ ]
DT =	4.1868 × m ×γ		Dt [0		Ñ ],Kèëè Kt	=		[ñ ]
	4.1868 × m ×γ						P		.	(7.37)
						Ò			.	(7.37)
						Ò

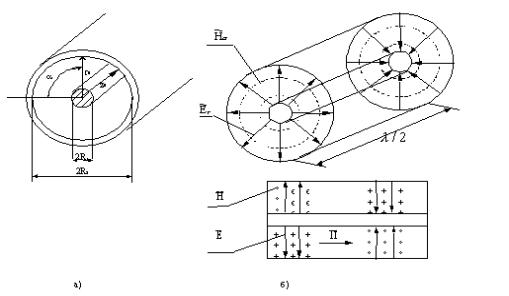
Коаксиальная линия (рис.7.7) относится к передающей линии, в которой может, с одной стороны, распространяться тип волны T , а с другой стороны, более сложные волны, имеющие поперечные и продольные составляющие

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2821 22 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023196.13 Кб3Электромагнитная экология..pdf
#
05.02.2023652.23 Кб18Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб14Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб46Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб19Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб38Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб41Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб50Электромагнитные поля и волны..pdf
#
05.02.20233.12 Mб26Электроника 1. Физические основы электроники-1.pdf
#
05.02.20231.01 Mб10Электроника 1. Физические основы электроники.pdf
#
05.02.2023688.65 Кб7Электроника 2. Электронные приборы.pdf