Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Электромагнитные поля и волны.-5

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

3.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

109

Ответ: j = - r0 × x 2 + A × x + B . 2 × e

Задача № 41 Каково будет выражение для плотности энергии электростатического поля и его потенциала?

Ответ: v = D 2 , E = -gradj .

2 × e

ϕ1 = 0

2R1 2R2

ϕ 2 = U 0

Рис. 3.25

Задача № 42 Как записать выражение, соответствующе полю, изображенного на рисунке 3.25 цилиндри-ческого конденсатора?

			ln		r
Ответ: j = U 0		×			R1	.
Ответ: j = U 0		×				.
			ln	R2
			ln		R1
					R1
Задача № 43 В безграничной среде задано распределение
заряда r = r0	2 ,	где			r0 - постоянная величина, а r - сферическая
r

координата. Каким будет распределение потенциала?

Ответ:

j = - r0

× ln r +

+ C2 .

Задача

№

Каков

потенциал ϕ ,

создаваемый

точечным

зарядом,

расположенным

над

идеально

проводящей

плоскостью, в точке M (рис.3.26)?

Рис. 3.26

Ответ: j =

6 × p ×e × a

Задача № 45 Определите возможные значения

ϕ = 0

произвольных

постоянных

объёме

V .

j = (C

× e − r + D

× e r )× (A × cos l × r + B

× sin l × r ) где

( n - целое число) см. рис. 3.27.

ϕ = U

Ответ:

Dλ = Aλ

= 0, l = 2 × n .

ϕ = 0

Рис. 3.27

110

Задача № 47 Над проводящей равномерно заряженной

плоскостью с зарядом ξ на единицу площади помещают положительный заряженный провод с зарядом τ на единицу

длины. На каком расстоянии сила, действующая на провод, будет

равна нулю?

Ответ: h =

4 × p × x

Задача

№

48 Определить ёмкость

двухпроводной линии на единицу длины этой

линии (см. рис. 3.28. Считать D >> R (потенциал

2- х

проводной

линии

определен

как

Рис. 3.28

j =

× ln

× p × e

Ответ: C = p × e × ln D

Задача № 49 Какой из приведенных ниже векторов может быть вектором напряженности электростатического поля?

Ответ: A = y × z ×i + x × z × j + x × y × k .

3.3.2. Цилиндрический конденсатор

Задача № 50 Два коаксиальных металлических цилиндра радиуса

R1 и R 2 разделены слоем диэлектрика с диэлектрической проницаемостью ε . На внешний цилиндр подан потенциал U , внутренняя пластина заземлена (рис. 3.29). Найти распределение

потенциала

между цилиндрами,

а также Е, D,ξ ,С. Краевыми

эффектами пренебречь.

Ответ:

j =

U ×ln(r / R1 )

= εE

ln(R2 / R1 )

dϕ

= -

r × ln(R 2 / R1 )

ξ = −ε U

/(ln(R

/ R

) при r = R

= -e U

/(ln(R

/ R

)

при r = R

R 2

Рис.

R1 и R 2

111

q = ξ 2πR1L = ξ2 2πR2 L , C = ε 2πL /(ln(R 2 / R1 ) .

3.3.3. Сферический конденсатор

Задача № 51 Конденсатор, состоящий из двух проводящих концентрических сфер с радиусами находится под потенциалом U ,

поданным на внешнюю сферу. Внутренняя сфера заземлена. Пространство между сферами заполнено

Рис.

воздухом (см. рис. 3.30).

Найти ϕ(r) , Е, D,Q,C.

Ответ:

ϕ =

UR1 R2

r − R1

при

r = R

, ϑ = U ,

при

R2 − R1

R1r

r = R1 ,ϑ = 0.

dϕ

UR1R2 1

Ey = −

= −

, Dy = ε

0 Ey = −ε0

R − R

ξ = −ε

UR2

, Q = ξ 4π R2 , C = ε

4π R2 R1

0 R − R R2

0 R − R

3.4. Контрольные вопросы

1.Дать определение электростатическому полю. Чем оно создается?

2.Чем описывается электростатическое поле ?

3.Какое уравнение является основным для нахождения потенциала?

4.Во что преобразуется в уравнение Пуассона?

5.Что показывает закон Кулона?

6.Как ведут себя тангенциальные составляющие электрического поля при прохождении из одной среды в другую?

7Как записываются нормальные составляющие электрической индукции при

прохождении из одной среды в другую, когда на границе существует поверх-ностный заряд?

112

8.Как определяется напряженность электрического поля при известной силе взаимодействия двух зарядов?

9.Как определяется напряженность электрического поля для точечного заряда?

10.Чему равна работа на перемещение заряда на пути dl ?

11.Чему равен потенциал в произвольной точке М?

12.Для чего применяются уравнения Пуассона и Лапласа?

13.Что определяет принцип суперпозиции при решении электростатических задач?

14.Как определяется энергия электростатического поля?

15.Как определяется емкость системы, состоящей из двух заряженных проводников?

113

Глава 4. Электромагнитное поле постоянных токов

Целью данного занятия является закрепление теоретического материала путем решения задач по следующим вопросам курса:

∙Электрическое поле постоянного тока.

∙Магнитное поле постоянного тока.

∙Индуктивность и взаимная индуктивность.

∙Энергия магнитного поля.

4.1.Электрическое поле постоянного тока

Для случая постоянного тока ( j ¹ 0, ¶ / ¶t = 0) стема уравнений Максвелла для электрического поля имеет вид:

		rotE = 0 , divD = ρ ,				D = ε E ,	R		(4.1)
							j ÏÐ = σ E
Первое уравнение (4.1) показывает, что
электрическое		поле		постоянного			тока
подобно	электростатическому					полю
потенциально.		Но		в	отличие			от
электростатического.			оно		существует		и	в
проводящей	среде,		где		R	Если		по
					E = j / σ .
проводнику	протекает			ток, то		на	его		Рис.
поверхности появляется отличная от нуля

тангенциальная		(касательная)				составляющая			напряженности
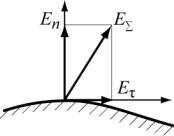
электрического		поля	E	(см. рис. 4.1).				Отношение нормальной

составляющей Еn к тангенциальной Еτ для хороших проводников имеет порядок 105 , и Еτ пренебрежимо мало по сравнению с Еn .

При вычислении электрического поля в идеальном диэлектрике, окружающем проводник с постоянным током, можно пренебречь касательной составляющей напряженности электрического поля и считать, что электрическое поле в нем почти не отличается от электростатического.

Иное наблюдается внутри проводника. При наличии постоянного тока в проводящей среде существует электрическое поле, которое описывается следующей системой дифференциальных и интегральных уравнений :

	114
rotE = 0 ,	divj =	0 ,	R	= σ E .
rotE = 0 ,	divj =	0 ,	j ÏÐ	= σ E .
R R	= 0
∫ EdL	= 0	R
L	, ∫	jdS = 0 .

( 4.2)

(4.3)

Сопоставим систему уравнений (4.2) и (4.3) с уравнениями электростатического поля в среде, не содержащей зарядов,

R	R		R	R
rotE = 0 ,	divD = 0 ,		R	R	(4.4)
rotE = 0 ,	divD = 0 ,		D = ε E ,		(4.4)
R R
∫ EdL	= 0	R			(4.5)
L	, ∫ D dS = 0 ,				(4.5)
L
	S

Видим, что они совершенно одинаковы по форме. Уравнения электростатики (4.4) и (4.5) становятся справедливыми для электрического поля в проводящей среде, если электрическую

индукцию D заменить в них плотностью тока j , а диэлектрическую проницаемость ε – удельной проводимостью σ σ.

R	(4.6)
D → j и ε →σ .

Однако, тождественность уравнений еще не гарантирует тождественности их решений. Для этого необходимо также совпадение граничных условий.

Это совпадение имеет место только в слабо проводящих средах на границах с хорошими проводниками. Действительно, как следует из второго уравнения (4.3), нормальная составляющая j на границе двух сред непрерывна

j1n = j2 n .	(3.7)
Касательные составляющие в силу непрерывности Еτ	(E1τ = E2τ )
связаны соотношением
( j1τ / σ1 ) = ( j2τ / σ 2 ) .	(3.8)

При достаточном различии проводимостей σ1 и σ 2 составляющей j1σ можно пренебречь и считать вектор j1 нормальным к границе.

Таким образом, совпадение граничных условий для векторов D в электростатике и j в проводящих средах имеет место только на границах хороших проводников (металлов) и слабо проводящих сред. В этих случаях решение соответствующей электростатической задачи может быть использовано для

115

определения поля в слабо проводящей среде. В литературе этот метод называется методом электростатической аналогии.

Применительно к системе двух проводников (конденсатору) этот метод приводят к следующему соотношению между емкостью идеального (без потерь) конденсатора и проводимостью того же конденсатора но с потерями

C	=		ε
G	=		σ	(3.9)

Это соотношение обычно используется для вычисления сопротивления изоляции между хорошими проводниками.

4.2. Магнитное поле постоянного тока

	Для	случая	постоянного	тока	( j ¹ 0 , ¶ / ¶ t = 0 )			система
уравнений Максвелла для магнитного поля имеет вид:

	Уравнения		Максвелла в	Уравнения			Максвелла в
	дифференциальной форме			интегральной форме
					R
	rotH = j			∫ Hdl		= I
		R		L
	divB = 0			L	R
	divB = 0				R
	B = μH			∫ BdS = 0 (4.11)
				S

	Если в области нет токов (магнитостатика), то в уравнениях
(4.10) и		(4.11) нужно положить		j = 0	и	I = 0 .	В этом	случае

магнитное поле оказывается потенциальным и напряженность магнитного поля можно представить в виде:

	R
	H = − grad ϕ M ,	(4.12)
где jM - магнитостатический	потенциал,	который подчиняется
уравнению
Лапласа:
	Ñ2jM = 0 .	(4.13)

В тех случаях, когда в рассматриваемой области имеется ток ( j ¹ 0) магнитостатический потенциал ϕM становится неоднозначной функцией. Разность значений между точками K1 и K2 зависит от контура, по которому выполняется интегрирование в формуле

116

K 2	R R
ϕ1M − ϕ2M = ∫	Hdl	(4.14)
K1	,	(4.14)
K1
а именно, при каждом обходе	контура вокруг	тока I в

положительном направлении (так, чтобы контур образовывал с направлением, в котором течет ток, правовинтовую систему) значение интеграла в (4.14) возрастает на величину I .

Таким образом, магнитостатический потенциал ϕM не позволяет установить однозначно связь между стационарным магнитным полем и создающим его постоянным током. Для определения магнитного поля обычно вводят векторный потенциал A , связанный с вектором B соотношением

B = rotA	(4.15)
Векторный потенциал стационарного поля удовлетворяет
векторному уравнению Пуассона
Ñ2 A = -mj .	(4.16)

Если токи сосредоточены в ограниченной области V , на поверхности S или протекают по контуру L , то решение уравнения (4.16) можно получить из соответствующей формулы для:

объемных

поверхностных

линейных

токов

μ I

∫

A =

(4.19)

A =

∫

(4.17)

4π

4π v R

(4.18)

где R - расстояние от элементов dv, dS

или dl

до точки,

в которой

вычисляется потенциал.

Переход

от

векторного

потенциала

к напряженности

магнитного

поля

H производится

по

формуле

(4.15).

Предположение, что пространство заполнено однородной изотропной средой приводит к следующим вариантам закона Био – Савара в интегральной форме

Для объемных	Для	Для линейных

117

токов

поверхностных токов

токов

R R

[j , r0 ] dV

[jS , r0 ]dS

[dL, r0 ]

H =

4π ∫

R 2

4π ∫

(4.20)

(4.21)

(4.22)

Дифференциальная

форма

закона

Био –

Савара

для

линейных токов представляется в виде

R R

[dl , r0

4πR2

(4.23)

В таком виде закон Био-Савара определяет магнитное поле

в точке М , создаваемое элементом тока IdL (см. рис. 4.2).

Рис.

4.3. Энергия магнитного поля постоянного тока

Известно, что с магнитным

полем в объеме V

связана

магнитная энергия

R R

W M =

∫

BHdV

∫ μH 2 dV

(4.24)

с плотностью энергии

wì

= μH 2

(4.25)

С учетом (4.15) и (4.16) выражение (4.24) приводится к виду

W M =

∫

AjdV

(4.26)

где магнитная энергия представлена через объемные токи и векторный потенциал. В случае линейных токов выражение для

118

энергии магнитного поля упрощается. Например, формула (4.26) с учетом (4.19) для уединенного контура L с током I примет вид

W M =			1		∫	R R
						AdL

	2				L	.		(4.27)

Применим к интегралу в (4.27) теорему Стокса (1.26), получим
R						R
∫ AdL	= ∫ rot AdS = ∫ BdS						= Ô	(4.28)
L	S					S	,

где Ф – магнитный поток через поверхность S , опирающуюся на
контур S . Подставив (4.28) в (4.27), получим
	WМ = I ×Ф / 2 .							(4.29)
В случае N N контуров выражение для WМ записывается:
		1			N
	W M =			∑InÔ n
								(4.30)
		2 n=1				,

где Фn - поток магнитной индукции, пронизывающий контур Ln , In

-ток в контуре Lп.

4.4. Индуктивность и взаимная индуктивность

Так как поток магнитной индукции

Ф = L × I	(4.31)
пропорционален L – индуктивности контура, то
W М = I ×Ф / 2 = LI 2 / 2	(4.32)
В случае N контуров поток Фnk пропорционален току Ik :
Фnk = M nk Ik	(4.33)
Коэффициент пропорциональности M n k при k ¹ n	называют

взаимной индуктивностью контуров Lk и Ln , а коэффициент M kk -

собственной	индуктивностью				контура	Lk	Взаимная
индуктивность определяется следующим выражением
	Mnk =	μ	∫ ∫		d ln d lk
	Mnk =		∫ ∫		r
		4π L L			r		(4.34)
			n	k			(4.34)
			n	k

Формула симметрична относительно индексов n и k . Это значит, что совершенно такое же выражение будет получено и для взаимной индуктивности M kn , определяемой равенством

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 2812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023196.13 Кб1Электромагнитная экология..pdf
#
05.02.2023652.23 Кб9Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб6Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб29Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб7Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб24Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб30Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб33Электромагнитные поля и волны..pdf
#
05.02.20233.12 Mб16Электроника 1. Физические основы электроники-1.pdf
#
05.02.20231.01 Mб9Электроника 1. Физические основы электроники.pdf
#
05.02.2023688.65 Кб7Электроника 2. Электронные приборы.pdf