
Твердотельная электроника.-3
.pdf
226
Идеальный омический переход должен иметь прямолинейную и симметричную ВАХ (рис.3.16).
I
U
Рисунок 3.16. ВАХ идеального омического перехода
Реальные омические переходы обычно имеют более сложную структуру (рис.3.17).
М
n+ n
Рисунок 3.17. Структура реального омического перехода
227
4. ЭЛЕКТРОННО-ДЫРОЧНЫЕ ПЕРЕХОДЫ
4.1. Виды электрических переходов при контакте полупроводников
В твердотельной электронике используются следующие варианты контактов полупроводниковых слоев:
контакт полупроводников с одним типом проводимости, но с различным уровнем легирования (n+ - n, p+ - p),
контакт полупроводников с различным типом проводимости (p - n, p+ - n, n+ - p). При этом контактирующие слои могут иметь либо одинаковую ширину запрещенной зоны, либо изготавливаться на основе полупроводников с различной шириной запрещенной зоны. В зависимости от того, какие слои образуют электрический переход, их подразделяют нагомопереходы и гетеропереходы.
Гомопереход - это электрический переход на контакте полупроводников с одинаковой шириной запрещенной зоны.
Гетеропереход - это электрический переход на контакте полупроводников с различной шириной запрещенной зоны.
В свою очередь гомо- и гетеропереходы делятся на изотипные (n+ - n, p+ - p) и анизотипные (p - n, p+ - n, n+ - p).
Основой современных твердотельных приборов являются анизотипные гомопереходы. Их теория хорошо разработана. Поэтому вполне логично первоначально рассмотреть свойства таких переходов, а затем на базе этих знаний ознакомиться с теорией и применением гетеропереходов.
Таким образом, данный раздел учебного пособия посвящен в основном изучению анизотипных гомопереходов.
4.2. Механизм образования электронно-дырочного перехода. Определение электронно-дырочного перехода
Представим, что два полупроводника с различным типом проводимости приведены в тесное соприкосновение ,такчто между слоями p- и n-типа проводимости становится возможным обмен носителями зарядов (рис.4.1). В силу того, что в p-
полупроводнике концентрация дырок pp0 много больше, чем

228
концентрация дырок в n-слое pn0 , возникает процесс диффузии дырок из полупроводника p-типа в слой n-полупроводника. По аналогичной причине (nn0 >> np0 ) электроны из полупроводни-
ка n-типа проводимости диффундируют вp-полупроводник. В приконтактной области образуются нескомпенсированные слои с положительно заряженными донорами (в слое n-типа) и отрицательно заряженными акцепторами (в слое p-типа). Возникшее
диффузионное движение основных носителей должно было продолжаться до исчезновения градиента концентрации. Однако возникшее в области контакта электрическое поле, которое называется диффузионным или более точно полем контактной разности потенциалов, направлено так, что и для электронов и для дырок оно является тормозящим. Когда величина внутреннего электрического поля E станет достаточно большой, диффузионные потоки электронов и дырок прекратятся и структура придет в состояние термодинамического равновесия.
N а- |
|
P |
N д+ |
|
|
|
|
||
|
|
|
|
|
P |
- |
|
+ |
n |
|
|
|
||
P p 0 >> |
- |
|
+ |
Pn 0 |
- |
|
+ |
||
n p0 |
- |
|
+ |
<< n n 0 |
- |
|
+ |
||
|
|
|
n |
|
|
|
|
E |
|
|
|
|
|
|
ОПЗ
Рис. 4.1. К механизму образования электронно-дырочного перехода
Электронно-дырочный переход (ЭДП) - это переходная об-
ласть на контакте полупроводников с различным типом проводимости, отличительной особенностью которой является наличие внутреннего электрического поля.
229
4.3. Контактная разность потенциалов jko . Зависимость jko от температуры, ширины запрещенной зоны, концен-
трации легирующей примеси
Возникающее в переходном слое на контакте полупроводников с различным типом проводимости электрическое поле является тормозящим для основных носителей. Из-за этого для основных носителей возникает потенциальный барьер, величина которого определяется напряженностью электрического поля в p-n переходе. Лучше всего потенциальный барьер для основных носителей зарядов показать, используя зонную энергетическую диаграмму электронно-дырочного перехода.
Поскольку в дальнейшем достаточно часто используются зонные диаграммы p-n переходов, то необходимо записать порядок изображения таких диаграмм. Он следующий.
Изображаются границы ОПЗ.
Задается положение уровня Ферми в полупроводниках. При этом надо помнить, что в состоянии термодинамического равновесия уровень Ферми в полупроводниках p- и n-типов находится на одной горизонтальной линии. При приложении напряжения происходит смещение уровней Ферми относительно друг друга на величину приложенного напряжения. Причем уровень Ферми в полупроводнике, к которому приложен отрицательный потенциал, лежит выше, чем в полупроводнике, находящемся под положительным смещением.
Изображается зонная диаграмма полупроводниковp- и n-типов вне зоны ОПЗ.
Проводятся линии, соединяющие уровни Ec и Ev полупровод-
ников p- и n-типов. Эти линии находятся в ОПЗ p-n перехода. На рис.4.2 изображена зонная энергетическая диаграмма p-n
перехода в состоянии термодинамического равновесия. Барьер jko для основных носителей заряда называется контактной раз-
ностью потенциалов. Величина этого барьера определяет потоки основных носителей зарядов вp-n переходе. Величина барьера
jko определяется напряженностью внутреннего электрического поля E , поскольку именно это поле препятствует перемещению

230
основных носителей: электронов из n-области в p-область и дырок из p-области в n-область. Электрическое поле существует только в ОПЗ.
|
|
плоскость металлурги- |
ческого контакта |
|
|
||
|
|
р |
|
|
n |
|
|
Ec |
|
|
|
|
j |
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
||
Ei |
|
|
|
|
к |
Ec |
|
|
jр |
|
|
|
|||
|
|
|
|
EF |
|||
EF |
|
|
jn |
|
|||
|
|
|
|
|
|||
EV |
|
|
|
|
|
Ei |
|
|
|
|
|
|
|
||
EV
E
Рис. 4.2. Зонная диаграмма электронно-дырочного перехода в состоянии термодинамического равновесия
Плоскость, где происходит смена типа проводимости, называется плоскостью металлургического контакта.
Запишем выражение для расчета jko . Из рис.4.2 видно, что jko = jp + jn . Значения j p и jn определяются следующим
образом: jn |
= EF - Ei ; jp = Ei - EF . |
|
|||
С учетом выражений (3.5 и 3.8) значения (EF - Ei )n |
и |
||||
(Ei - EF )p выглядят следующим образом: |
|
||||
jn = (EF |
- Ei )n = kT ln |
Nд |
|
|
|
ni |
(4.1) |
||||
|
|
||||

231
jp = (Ei - EF )p = kT ln Na
ni
Тогда выражение для jko примет следующий вид
j0 |
= kT ln |
Na Nд |
|
n2 |
|||
k |
|
||
|
|
i |
(4.2.)
Из выражения (4.2) можно получить еще ряд соотношений, позволяющих производить расчет jko . Поскольку при полной ионизации примеси nn0 = Nд , а pp0 = Na , тогда выражение
(4.2) принимает следующий вид
|
jo = kT ln |
|
nn0 pp0 |
. |
|
|
|
|
|
|
|
|||||||
|
|
n 2 |
|
|
|
|
|
|
|
|||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(4.3) |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
С учетом закона |
действующих |
масс для |
|
полупроводников |
|||||||||||||
n - типа |
(nn0 pn0 |
= ni |
2 ) |
и p -типа |
(pp0np0 = ni |
2 ) выражение |
||||||||||||
(4.2) принимает вид |
|
|
|
|
|
|
|
|
|
|
||||||||
|
jko = kT ln |
pp0 |
|
|
jko |
= kT ln |
n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
n0 |
|
|
|
(4.4) |
||||||
|
pn0 |
|
|
np0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Наконец, |
учитывая, |
что |
|
значения n 2 можно |
определять, как |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
2 |
|
æ |
|
DE |
ö |
|
|
|
|
|
|
|
||||||
ni |
= Nc Nv expç- |
|
|
|
|
|
|
÷ , формула (4.2) представляется в виде |
||||||||||
|
kT |
|
|
|||||||||||||||
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|||||
|
jko = DE - kT ln |
Nc Nv |
. |
|
|
(4.5) |
||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
Nд Na |
|
|
|
|||||||
Из анализа выражений (4.2)-(4.5) можно сделать следующие выводы.
Высота потенциального барьера jko зависит от концентрации
легирующей примеси в полупроводниках p- и n-типов. Действительно, при изменении концентрации примеси в полупроводнике изменяется положение уровня Ферми. Для невырожденного

232
n - полупроводника значение jn может изменяться практически от нуля до DE / 2 . В полупроводнике p-типа от нуля до DE / 2 . Из чего следует, что максимальное значение jko для p - n пе-
реходов на основе невырожденных полупроводников не может быть больше ширины запрещенной зоны полупроводника DE .
Значение барьера jko зависит от температуры. Учитывая, что с увеличением температуры уровень Ферми приближается к середине запрещенной зоны, значения jn и j p будут уменьшаться.
Следовательно, величина барьера jko также уменьшается с ростом температуры. Это является одной из причин очень сильной
температурной |
зависимости |
параметров полупроводниковых |
||||||
приборов на основе p-n переходов. |
|
|
|
|||||
Высота потенциального барьера jko |
определяется шириной за- |
|||||||
прещенной |
зоны |
полупроводника, |
из |
которого |
изготовлены |
|||
p - n переходы: чем больше DE , тем выше барьер jko . Типич- |
||||||||
ные значения jko |
для переходов |
из |
германия |
составляют |
||||
(0,3 ¸ 0,5) |
В, |
для |
кремниевых – (0,6 ¸ 0,8) В. На рис.4.3 пред- |
|||||
ставлена |
зависимость jko для |
резких p-n переходов |
из различ- |
|||||
ных материалов от концентрации примеси в слаболегированной области p-n перехода.
jк0
GaAs Si
Ge
 Nд
Nд
Рисунок 4.3. Зависимость j к0 от концентрации примеси в слабом
4.4. Потоки носителей зарядов в ЭДП по энергетическим диаграммам. Односторонняя проводимость p-n перехода
233
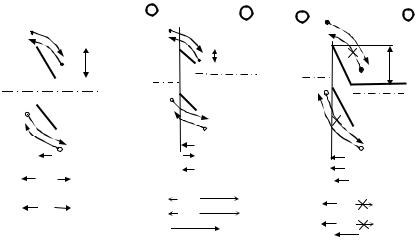
Для понимания основного свойства электронно-дырочного перехода - явления односторонней проводимости, необходимо рассмотреть движение носителей заряда в переходе. Лучше всего это сделать с использованием зонных энергетических -диа грамм p-n перехода. Рассмотрим движение носителей зарядов для состояния термодинамического равновесия, когда напряжение на переходе равно нулю (U = 0), при приложении прямого
(U > 0) и обратного смещения (U < 0). Под прямым смещением на p-n переходе понимается такое смещение, когда отрицательный потенциал от источника питания прикладывается к по-
лупроводнику n-типа. |
|
|
|
|
|
|
|
дляU = 0 , U > 0 |
|
|
|||||||||||||||||
|
На рис.4.4 представлены диаграммы |
и |
|||||||||||||||||||||||||
U < 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
u = 0 |
|
|
|
|
|
|
|
u > 0 |
|
|
|
|
|
u < 0 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
- |
|
|
- |
|
nn0 |
|
+ |
|
|||||
|
n p 0 |
|
|
|
|
|
|
|
Ec |
n p |
0 |
nn |
|
|
|
|
|
|
np0 |
|
nn0 |
|
|
||||
|
|
|
|
|
|
jк0 |
|
|
|
0 |
jк0 - u |
Ec |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
nn0 |
|
|
|
|
|
|
|
|
|
|
|
j к0 +u |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Ec |
EF |
|
|
|
|
|
|
|
EF |
EF |
|
|
|
|
Ec |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
EF |
|
|
|
|
|
|
|
Ev |
|
|
|
||||||||
|
|
|
|
|
|
|
|
Ev pp0 |
|
|
|
|
|
|
|
|
|
EF |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ev |
|
|
pp0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
pp |
|
|
|
|
|
|
|
Ev |
|
|
|
E |
|
pn0 |
|
|
|
|
|
|
|
|
Ev |
|||
|
0 |
|
|
p |
n0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
pn0 |
|
||||
|
|
|
|
|
|
|
|
|
Eвн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
jpn 0 |
|
|
jp p |
|
|
ES |
|
|
|
|
Eвн |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
j |
|
|
|
|
|
0 |
|
|
jpn 0 |
|
|
|
|
jp p0 |
|
|
jpn 0 |
ES |
jp p0 |
|||||||
|
|
|
|
|
jn |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
np0 |
|
|
|
|
|
|
|
|
j |
|
|
|
|
j |
|
|
|
|
||||||||
|
|
|
j=0 |
|
n0 |
|
np0 |
|
jпр |
|
nn0 |
|
jnp0 |
|
|
j |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jобр |
nn0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a) |
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
||
Рисунок 4.4. Зонные энергетические диаграммы p-n перехода в состоянии термодинамического равновесия (а), при прямом (б) и обратном смещении (в)
234
Для правильного понимания сущности работы ЭДП необходимо при рассмотрении вопроса помнить и руководствоваться уравнением полного тока: токи в полупроводнике образуются за счет движения электронов и дырок, а перемещаться они могут за счет сил электрического поля и градиента концентрации носителей.
При U = 0 под действием сил внутреннего электрического поля неосновные носители np0 , pn0 втягиваются в ОПЗ перехо-
да и, |
перемещаясь, создают токи неосновных носителей jn p 0 и |
jpn 0 . |
Эти токи малы, поскольку концентрации неосновных но- |
сителей невелики. Для основных носителей (nn0 , pp0 ) внутрен-
нее поле является тормозящим. Оно создало барьер jko для этих
носителей. И все же, поскольку носители в невырожденных полупроводниках подчиняются статистике Больцмана, то некоторая незначительная часть носителей способна преодолеть барьер
jko и создать токи основных носителей jp p 0 и jnn0 . Рис.4.5 ил-
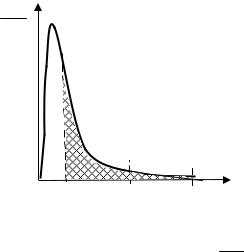
люстрирует распределение носителей по энергиям по статистике Максвелла-Больцмана. Ток основных носителей приU = 0 создается носителями, имеющими энергию W > jko . Поскольку таких носителей мало, то и токи jp p 0 и jnn0 невелики.
В состоянии термодинамического равновесия токи основных носителей и токи неосновных носителей равны и противо-
положно направлены. Суммарный ток через p - n |
переход ра- |
вен нулю. |
|
При приложении прямого смещения(U > 0), |
поскольку |
вектора внутреннего поля E и поля от внешнего источника Eвн |
|
противоположно направлены, суммарное поле |
в переходе |
уменьшается, что приводит к понижению барьераjko на вели-
чину приложенного напряжения.
В результате диффузионные потоки основных носителей резко возрастают, давая значительные токи jnn0 .
235
В этом случае через барьер (jko -U ) может перейти значитель-
ное количество носителей(заштрихованная область справа от
(jko -U ) на рис.4.5).
Так как функция распределения Максвелла-Больцмана экспоненциальна, то это означает, что при понижении барьера jko
потоки основных носителей возрастают по экспоненте. Таким образом, при приложении прямого смещения ток черезp-n переход определяется движением основных носителей заряда за счет их диффузии.
dN
dW
j0 |
-U j к0 |
W |
jк0 +U |
||
к |
|
|
Рис. 4.5. Распределение носителей заряда в полупроводнике,
приходящееся на единичный интервал энергий dN от энергии dW
W по статистике Максвелла-Больцмана.
Он достаточно большой по величине и по экспоненте изменяется от приложенного напряжения.
С увеличением прямого смещения уменьшается суммарная напряженность электрического поля в p-n переходе. При этом уменьшается глубина проникновения поля в области полупро-
