Твердотельная электроника.-3

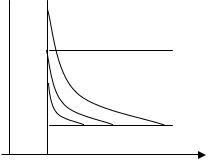
266

ния: у германиевых приборов ток насыщения значительно больше чем у кремниевых приборов.

4.10. Явления в электронно-дырочном переходе при высоком уровне инжекции.

Прежде всего введем понятие высокого уровня инжекции. Если граничная концентрация инжектированных носителей pn

в несимметричном p + - n переходе мала по сравнению с кон-

центрацией основных носителей nno ( pn << nno ), то это соответствует низкому уровню инжекции (рис.4.24).

Если pn >> nno , то это соответствует высокому уровню ин-

жекции. При высоком уровне инжекции вp-n-переходе возникают сле дующие явления:

1. В базе p-n перехода возникает внутреннее электрическое поле;

n

P+ Pn Е

nn0

3

2

1

pn0

X

Рисунок 4.24. Распределение концентрации инжектированных носителей в базе диода при низком (1), среднем (2) и высоком (3) уровне инжекции

Увеличивается концентрация основных носителей в базе на границе p-n- перехода;

Уменьшается сопротивление базы; Изменяется характер протекания тока.

Рассмотрим подробнее каждое их указанных явлений.

267

Инжекция значительного количества дырок в базу нарушает условие электронейтральности базы. Для того чтобы восстановить электронейтральность электроны начинают подтягиваться к границе p-n- перехода. Поскольку база легирована однородно,

то градиент концентрации электронов отсутствует. Тогда необходима сила, которая заставляет электроны перемещаться к гра-

q Dn и сокращая Dn , kT

E = - KT × 1 × dnn q nn dx

(4.53)

Необходимо отметить, что условие электронейтральности в базе выполняется, если pn - pno » nn - nno или, с учетом того, что pn >> pno

pn » nno - Nq

(4.54)

Причем надо иметь в виду, что равенство (4.54) является приблизительным, так как для поддержания неравномерного распределения основных носителей в базе необходимо электрическое поле, которое и возникает из-за неполной компенсации заряда неосновных носителей вблизи p-n-перехода. Кроме электрического поля, возникающего из-за неполной компенсации, существует еще одна компонента, связанная с падением напряжения на базе диода при протекании тока. Выражение напряженности, определенное по (4.53) включает обе составляющие и с учетом условия электронейтральности(4.54) принимает вид

(4.55)

268

(4.55)

Эффект уменьшения сопротивления базы при высоком уровне инжекции очевиден: при высоком уровне инжекции концентрация неосновных носителей, особенно в p - n переходах с

тонкой базой, высока и сопротивление слаболегированного слоя уменьшается. Кроме этого надо отметить, что высокий уровень инжекции вызывает изменение времени жизни и подвижности носителей, и условий на омическом контакте.

Наконец, при высоком уровне инжекции изменяется характер протекания тока: кроме диффузионной составляющей появляется дрейфовая составляющая, обусловленная наличием внут-

реннего поля в базе. Запишем выражения для ВАХ p+ - n перехода для случая, когда W << L , при высоком уровне инжекции. Так как в p+ - n переходе электронным током можно пренебречь, тогда ток, обусловленный диффузией и дрейфом дырок равен:

(4.57)

С учетом соотношения pn >> Nq (nno )уравнение (4.57) принима-

ет вид jp = -q2Dp dpn , dx

(4.58)

Тогда с учетом того, что U = U p-n +U Б , получим

exp qU >>1 запишем окончательное выражение для ВАХ при

2kT

высоком уровне инжекции.

перехода с тонкой базой, где вместо коэффициента диффузии D стоит удвоенный коэффициент, а вместо напряжения U в

экспоненте записано U , отражающее факт падения напряжения

2

в среднем пополам между ОПЗ и базой.

Несколько замечаний по поводу применимости формулы (4.64). Нижняя граница определяется исходя из непрерывности хода ВАХ при переходе от низкого к высокому уровню инжекции. Приравнивая выражения (4.40) и (4.64), получим:

272

В p-n-переходах с толстой базой, когда W >> L , сопротивление базы можно считать не зависящим от тока, т.е. пренебрегать модуляцией сопротивления базы. Тогда ВАХ p - n перехода может быть представлена в виде:

где Rб - сопротивление базы p-n-перехода

Если сопротивление Rб известно, то рассчитать ВАХ мож-

но, принимая в качестве независимой переменной значение тока

I .

При больших токах, когда напряжение на переходе прибли-

жа-

ется к контактной разности потенциалов jk 0 и как бы стабили-

зи-

руется, ВАХ p-n-перехода с толстой базой можно записать так

U = jk 0 + IRб .

Это говорит о том, что при U » jk 0 ВАХ становится близкой к

линейной, а не экспоненциальной, поскольку экспоненциальный характер ВАХ связан с экспоненциальной зависимостью концентрации инжектированных носителей от напряжения.

4.11. Диффузионная и барьерная ёмкости ЭДП

При подключении p-n-перехода к переменному источнику напряжения через него течет емкостной ток, что свидетельствует об емкостных свойствахp-n-перехода. Для описания емкостных свойств перехода вводится понятие диффузионной и барьерной емкостей.

Барьерная емкость - это емкость плоского конденсатора, мнимыми обкладками которого являются изменяющиеся границы ОПЗ, а функцию диэлектрика выполняет сама ОПЗ(рис. 4.25).

1 2 2 1

Рисунок 4.25. К понятию барьерной емкости p - n перехода

273

Барьерная емкость есть проявление токов смещения в p - n

переходе. Она определяется той долей тока, которая не связана с движением носителей заряда черезp - n переход. Действи-

тельно при приложении, например, прямого смещения границы ОПЗ смещаются так, что ширина его уменьшается, а при обратном напряжении - увеличивается.

При этом границы из плоскости 1 (соответствующие U = 0 ) смещаются в положения, соответствующие плоскости 2, (соответствующие U > 0 ), за очень короткий промежуток времени (10-14 -10-13 с). Смещение носителей и вызывает появление всплеска тока, который по своей природе является током смещения. Эти изменяющиеся границы ОПЗ принимаются за мнимые обкладки плоского конденсатора. Поскольку в ОПЗ подвижных носителей в идеальном случае нет, то ОПЗ можно считать диэлектрическим.

Значение барьерной емкостей Cб таким образом можно рас-

считать по формуле емкости плоского конденсатора

Cб = ee0 S , d

(4.67)

где S - площадь p - n перехода.

Подставляя в (4.67) выражение для ширины ОПЗ d , получим выражение для расчета Cб для резкого симметричного перехода

4.68)

Для резкого несимметричного p - n перехода

275

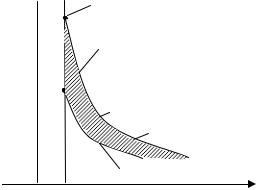
Более сложной для восприятия является диффузионная емкость. Для её понимания рассмотрим распределение концентра-

ции инжектированных в n - базу носителей в p+ - n переходе

(рис.4.28).

При U = 0 pn = pno

При увеличении напряжения до U1 и U 2 возрастает гранич-

ная концентрация p1n (0) и pn2 (0), и общая концентрация носителей в базе, т.е. происходит изменение заряда в базе p - n пе-

рехода при изменении напряжения на переходе. Можно записать, что

DQ = CD DU ,

Рисунок 4.28. К понятию диффузионной емкости p – n перехода