ПРИЛОЖЕНИЕ 3. РАСЧЕТНЫЕ ФОРМУЛЫ ДЛЯ КАСКАДА С НИЗКОЧАСТОТНОЙ КОРРЕКЦИЕЙ
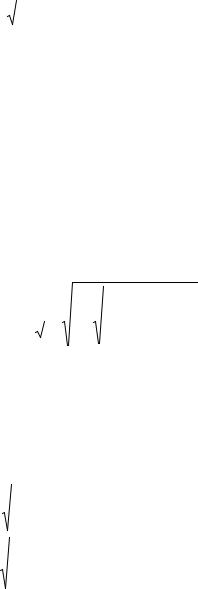
Емкость фильтра низкочастотной коррекции для получения оптимальной по Брауде частотной характеристики, имеющей максимальную протяженность горизонтального участка в области нижних частот (без подъема) рассчитывается по формуле
Cф |
= |
|
τнmopt |
; |
|
|
|
(П.3.1) |
||
|
|
|
|
|
|
|
||||
|
|
|
|
Rф |
|
|
|
|
||
|
|
= |
|
|
|
|
; |
|
||
m |
|
(1+ a)2 |
−(1+ 2ab)−ab |
(П.3.2) |
||||||
opt |
|
|
|
|
|
|
|
|
|
|
a = |
Rф |
; |
|
|
|
(П.3.3) |
||||
|
|
|
|
|||||||
|
RК |
|
|
|
|
|||||
b = |
|
|
|
RК |
; |
|
|
(П.3.4) |
||
(RК + RН ) |
|
|
||||||||
τн =СР(RК + RН ). |
(П.3.5) |
|||||||||
Если нагрузкой является следующий каскад, то RН представляет собой входное сопротивление следующего каскада с учетом базового делителя.
Расширение полосы пропускания в области нижних частот, которое дает коррекция за счет конденсатора Cф, рассчитанного по формуле (П.3.1), характеризуется коэффициентом
|
ωн |
|
1+ a |
|
|
|
|
2mopt |
|
2 |
|
|
|||
β = |
= |
1 |
+ 1 |
+ |
|
, |
(П.3.6) |
||||||||
ωнк |
|
|
|
(1+ a)2 |
|||||||||||
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ωн – нижняя граничная частота (на уровне 0,707) без коррекции, ωнK – то
же с коррекцией.
Формулы для относительного усиления и спадов плоской вершины импульса за счет СР и СЭ:
YнР = |
|
|
|
|
|
|
1 |
|
|
|
|
|
; |
|
|
|
|
|
|
(П.3.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
1 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(ωτн)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
YнЭ = |
|
|
|
|
1 |
+ |
(ωС |
Э |
R |
Э |
)2 |
|
; |
(П.3.8) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(1+SR |
|
)2 |
+(ωС |
R |
)2 |
|||||||||||||||||
|
tи |
|
|
|
Э |
|
|
|
|
|
|
|
Э |
Э |
|
|||||||
∆Р = |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(П.3.9) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
τн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∆Э = Stи ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(П.3.10) |
||||||
CЭ
где tи – длительность импульса.
68
ПРИЛОЖЕНИЕ 4. РАСЧЕТНЫЕ ФОРМУЛЫ ДЛЯ КАСКАДОВ С ВЫСОКОЧАСТОТНОЙ КОРРЕКЦИЕЙ
Параметры биполярного транзистора П-416А при JК0=2 мА:
S0=80 мСм, fr=60 МГц, gвх=0,92 мСм, CК=8 пФ, gi=0,036 мСм, rБ=50 Ом, τ=7,8 нс.
Проводимости цепей питания и нагрузок:
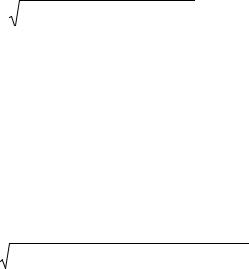
gК1=1,96 мСм; gК2=9,1 мСм; g = |
1 |
+ |
1 |
= 0,22 мСм; gН=0,83 мСм, |
|
R |
R |
||||
|
|
|
|||
|
10 |
|
11 |
|
где gК1 – проводимость коллекторной нагрузки первого каскада; gК2 – проводимость коллекторной нагрузки второго каскада;
g – проводимость делителя, включенного в цепь базы второго каскада; gН – проводимость внешней нагрузки первого каскада.
Коэффициент усиления в области средних частот K0 рассчитывается по формулам:
K0 |
= |
S0 |
|
(П.4.1) |
gi + gК1 |
|
|||
|
|
+ gН |
||
– при работе исследуемого каскада на внешнюю активную нагрузку,
K0 |
= |
S0 |
(П.4.2) |
||
gi + gК1 |
+ g + gвх2 |
||||
|
|
|
|||
– при работе исследуемого каскада на входное сопротивление каскада. Величина корректирующей индуктивности, обеспечивающая оптимальную частотную характеристику для каскада, работающего на
активную нагрузку, рассчитывается по формуле
|
|
|
|
|
L |
= |
|
|
1 |
|
−τ1(1−a)+ |
τ12(1−a)2 +(τ+τ1)2 (1−a2 ) |
, |
(П.4.3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
К |
|
|
gК1 |
|
|
|
|
|
|
1−a2 |
|
|
|
||||
где a = R |
(g |
i |
+ g |
Н |
), |
g |
0 |
= g |
i |
+ g |
К1 |
+ g |
Н |
= |
1 |
– |
эквивалентная проводимость |
|||||
R |
||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
выходной |
цепи |
|
исследуемого |
каскада |
по |
переменному току, |
τ1 =C0′R0 , |
|||||||||||||||
C0′ = CКS0rБ +СК +СМ +Свх g |
(СМ |
– емкость монтажа, равная 50 пФ; Свх.g – |
||||||||||||||||||||
входная емкость детекторной головки прибора Х1-7Б, около 4 пФ).
Для каскада, работающего на входное сопротивление следующего каскада, величина корректирующей индуктивности LК, обеспечивающая оптимальную частотную характеристику, определяется из выражения
L |
|
= |
−[τ1′(1−a)−τR0gвх2 ]+ |
[τ1′(1−a)−τR0gвх2 ]2 +(τ+τ1′)(1−a2 ) |
|
, (П.4.4) |
К |
|
gК1(1−a2 ) |
||||
|
|
|
|
|||
|
|
|
|
|
||
где |
|
|
a = R0(gi + g + gвх2 ); |
|
||
|
|
69 |
|
|
||
g0 = gi + gК1 + g + gвх2 = 1 ; R0
τ1′ = C0′R0 ;
C0′ =СК +CКS0rБ +СМ +Свх g +Cвх2
Свх2 = |
τ |
+ K02CК , |
(П.4.5) |
|
|||
|
rБ |
|
|
где K02 – коэффициент усиления второго каскада, который рассчитывается по формуле
K02 = |
S0 |
≈ |
S0 |
. |
(П.4.6) |
gi + gК2 |
|
||||
|
|
gК2 |
|
||
Величины корректирующих элементов RЭ, CЭ, обеспечивающих оптимальную частотную характеристику в каскаде с эмиттерной коррекцией при работе на активную внешнюю нагрузку, рассчитываются следующим образом
R = |
A1 −1 |
, |
(П.4.7) |
Э S0
где A1 – глубина последовательной отрицательной обратной связи по току эмиттера, которая показывает во сколько раз уменьшается коэффициент усиления каскада усилителя при введении в него отрицательной обратной связи
A |
= K0 |
= −1+ |
1+(m +1)2 |
, |
(П.4.8) |
|
1 |
K0′ |
|
m |
|
||
где K0 – коэффициент |
|
|
|
|||
усиления |
каскада без обратной связи, |
K0′ – |
||||
коэффициент усиления каскада усилителя при введении последовательной отрицательной обратной связи по току с глубиной
A1 =1+ S0RЭ ; |
|
|
|
(П.4.9) |
||||||
m = |
τЭ |
; |
|
|
|
|
(П.4.10) |
|||
|
|
|
|
|
||||||
|
|
|
τв |
|
|
|
|
|
||
τЭ =СЭRЭ ; |
|
|
|
(П.4.11) |
||||||
τв = τ+ τ1. |
|
|
|
|
(П.4.12) |
|||||
Для заданной глубины отрицательной обратной связи (А1=2), из |
||||||||||
выражения для А1 рассчитывается m: |
|
|
|
|
|
|
||||
|
|
−1+ 1+ |
A1 +1 |
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
A |
−1 |
|
|
|
m = |
|
|
|
|
|
1 |
|
|
. |
(П.4.13) |
|
|
|
A1 +1 |
|
|
|||||
|
|
|
|
|
|
|
|
|||
По известному значению m рассчитывается |
|
|||||||||
CЭ |
= mτв . |
|
|
|
|
(П.4.14) |
||||
|
|
|
RЭ |
|
|
|
|
|
||
При работе исследуемого каскада на входное сопротивление следующего каскада величины корректирующих элементов RЭ и СЭ рассчитываются следующим образом:
70
|
|
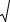
R |
= |
|
A1 −1 |
; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Э |
|
|
|
|
|
|
|
|
S0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
CЭ |
|
= − B + |
B2 − AC |
; |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ARЭ |
|
|
||||
|
|
A =1−k 2 ; |
|
|
||||||||||||||||||
|
|
B = a −kd ; |
|
|
||||||||||||||||||
|
|
C = 2b −d 2 ; |
|
|
||||||||||||||||||
|
|
K = |
|
1 |
|
|
|
; |
|
|
|
|
|
|
|
|
||||||
|
|
A |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a = |
|
τв |
; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
τв = τ+ τ1 + τ2 + τ3 ; |
|
|
||||||||||||||||||
|
|
τ1 =СКS0rБR0 ; |
|
|
||||||||||||||||||
|
|
τ2 = CК +СМ +Свх g R0 ; |
|
|
||||||||||||||||||
|
|
τ3 =Cвх2R0 ; |
|
|
||||||||||||||||||
|
|
b = |
|
|
τ |
(τ2 + τ3 )+ |
τRЭ |
(τ3 + τ4 ); |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
A1 |
|
|
|
|
|
A1rБ |
|
|
|||||||||
|
|
τ4 =СM R0 ; |
|
|
||||||||||||||||||
d = |
τв |
+ |
RЭR0τ |
(gК1 + g + gвх2 )+ |
S0RЭ |
(τ3 + τ4 ); |
||||||||||||||||
|
|
A1rБ |
|
|
|
|||||||||||||||||
|
A1 |
|
|
|
|
|
|
|
|
A1 |
||||||||||||
|
|
g0 = gi′ + gК1 + g + gвх2 ; |
|
|
||||||||||||||||||
|
|
gi = |
gi′ |
; |
|
|
|
|
|
|
|
|
||||||||||
|
|
A1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
R |
= |
|
1 |
. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
|
|
|
g0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
71
(П.4.15)
(П.4.16)
(П.4.17) (П.4.18)
(П.4.19) (П.4.20)
(П.4.21)
(П.4.22) (П.4.23) (П.4.24)
(П.4.25) (П.4.26) (П.4.27) (П.4.28) (П.4.29) (П.4.30)
(П.4.31)