Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Электромагнитные поля и волны.-4

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

4.03 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1912 13 14 15 16 17 18 19 > Следующая >>>

113

чается поляризация волны на выходе пластины для частот f1 и f2? Параметры феррита и значения частот приведены в задаче 4.3.16.

Ответ: На частоте 1,2 ГГц толщина пластины равна 9,96 см, на частоте 12

ГГц 7,12 см, отличаются направлением вращения вектора E .

114

5 ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ЭЛЕМЕНТАРНЫМИ ИЗЛУЧАТЕЛЯМИ

Вданном разделе рассматриваются темы

Элементарные излучатели в свободном пространстве;

Диаграммы направленности элементарных излучателей над идеально проводящей землей;

5.1 Краткие теоретические сведения

В курсе электродинамики рассматриваются три элементарных излучателя: электрический и магнитный диполи Герца и элемент Гюйгенса. Для определения электрических и магнитных полей, создаваемых излучателями, используются вспомогательные функции - электрический и магнитный векторные

запаздывающие потенциалы A и AM . Более распространен электрический по-

тенциал, который в дальнейшем будем называть просто векторным потенциалом. При известных токах возбуждения векторный потенциал определяется формулой

	μ		r		−ikr
v			j	e	−ikr
&			j	e
A(M ) =		∫		ст		dv ,	(5.1)
A(M ) =	4π	∫		r		dv ,	(5.1)
		V

где М-точка наблюдения, jст - плотность сторонних токов, являющихся источ-

ником электрических и магнитных полей, r – расстояние от точки объема V, где находятся токи jст и точкой наблюдения М, k – волновое число.

Диполем Герца называется отрезок проводника, длиной l , по которому протекает переменный электрический ток Iст, причем ток предполагается постоянным по длине диполя и l << λ . Для диполя Герца векторный потенциал определяется наиболее просто, как

r	μlI	стe	−ikr
A(M ) =	μlI	стe	,	(5.2)
		4πr

где r – расстояние от середины диполя до точки наблюдения.

115

Поместим диполь в центре сферической системы координат, расположив его вдоль оси «z» (рис. 5.1).

Поля Е и Н в точке М, определяемые через векторный потенциал (5.2), представляют в общем виде достаточно сложные функции сферических координат (r,θ,α). Для двух крайних случаев – ближней и дальней зон эти выражения существенно упрощаются.

Рис. 5.1

Ближняя зона определяется усло-

вием kr<<1, или

r<<l¤2p.

Комплексные амплитуды полей Е и Н в ближней зоне определяются вы-

ражениями:

ст

lIст

Hα

sinθ ;

= i

cosθ ; Eθ = i

sinθ ; (5.3)

4π

× r

2πωε × r

4πωε × r 3

Отметим характерные особенности полей в ближней зоне:

· Поля не имеют волнового характера, так как фазы полей не зависит от координат,

· Зависимость амплитуд полей в ближней зоне от координат такая же, как у электростатического диполя и отрезка проводника с постоянным током. Поэтому поля в ближней зоне называются квазистатическими. В частности, для них характерно быстрое убывание амплитуд полей с увеличением расстояния, как 1¤ r2 или 1¤ r3 .

· Поля Е и Н сдвинуты по фазе на 900 , поэтому среднее значение вектора Пойнтинга равно нулю. Это означает, что движение энергии вблизи диполя Герца носит колебательный характер.

Дальняя зона определяется условием kr>>1, или r>>l¤2p.. Комплексные амплитуды полей Е и Н в дальней зоне определяются вы-

ражениями:

116

klI

ст

−ikr

= i

sinθ × e ;

» 0 ;

Hα

4πr

(5.4)

klI

−ikr

= i

ст

Zc sinθ × e

;

Eθ

4πr

Характерные особенности полей в дальней зоне:

· Формулы (5.4) представляют поля в сферической волне, поскольку фа-

за полей постоянна на сфере с радиусом r. Вектора E и H перпендикулярны друг другу и направлению распространения волны.

·Амплитуды полей убывают с расстоянием как 1/r, то есть гораздо медленнее, чем в ближней зоне.

·Поля Е и Н синфазные и их отношение равно волновому сопротивлению данной среды для плоских волн – Zc. Среду будем считать идеальным диэлектриком (σ=0). Среднее значение вектора Пойнтинга (4.11) не равно нулю

Пср

(kI

cт

Zc sin 2

θ .

(5.5)

32(πr)2

Мощность, излучаемая диполем, может быть вычислена как интеграл по сфере в дальней зоне от Пср . Она может быть представлена в виде

P	=	1	I		2 R , -	(5.6)


∑	2			ст	Σ

где RΣ - сопротивление излучения диполя

R =	2πZc	( l	λ	)2	,	(5.6а)

Σ	3

l - длина волны в данной среде.

Зависимость амплитуд полей Е или Н в точке наблюдения от угловых координат при постоянном r называется амплитудной диаграммой направленности. Для диполя Герца диаграмма направленности описывается функция F (θ ) = sinθ . В полярной системе координат диаграмма направленности имеет вид тела вращения вокруг оси диполя (рис.5.2).

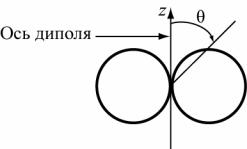
117

Магнитный диполь Герца – воображаемый диполь Герца, в котором вместо электрического тока протекает фик-

тивный магнитный ток I стм Переход от фор-

мул (5.3) и (5.4), определяющих поля диполя Герца, к соответствующим формулам для магнитного диполя Герца производится на ос-

нове принципа перестановочной двойственно-

Рис. 5.2	сти
	E « H, Iст « -Iстм , ε « -μ .	(5.7)
Магнитный диполь Герца может быть реализован в виде рамки c током
или щелевого излучателя малых размеров по сравнению с длиной волны.
Рамка с током эквивалентна магнитному диполю Герца, перпендикуляр-
ному плоскости рамки при выполнении условия
	Iстм l = -iωμ × I рS ,	(5.8)

где Iстм и l магнитный ток и длина диполя, I р и S - электрический ток и пло-

щадь рамки.

Расположим рамку в начале координат так, чтобы ее ось была направлена вдоль оси z. В дальней зоне поле рамки с током определяется формула-

ми (5.4) с учетом (5.7) и (5.8).

E =	I p k 2SZc	sinθ × e-kr	; H	θ	= -	Eα	.	(5.9)

α	4πr					Zc

Сопротивление излучения рамки определяется формулой

р		8π 3		S 2
RS	=		Zc		.	(5.10)
		3		λ4

Щелевой излучатель эквивалентен магнитному диполю Герца при усло-

вии, что длина щели много меньше длины волны, распределение вектора E по длине щели постоянно, магнитный ток диполя и напряжение на щели связаны

118

соотношением 2U щ = I cмт . При этом магнитный диполь располагается на по-

верхности щели, вдоль ее длины.

Элемент Гюйгенса – участок фронта плоской волны с размерами много меньшими длины волны. Элемент Гюйгенса эквивалентен взаимно ортогональным электрическим и магнитным диполям Герца, расположенным в плоскости фронта волны. (Рис.5.3)

Поле элемента Гюйгенса в дальней зоне, в сферической системе координат, представляется в виде

× S

−ikr

E = -i

(1 + cosθ )(θ0 cosα - α0 sinα )e

2λr

(5.11)

× S

−ikr

H = -i

(1 + cosθ )(θ

0 sinα + α

0 cosα )e

2λrZc

Рис.5.3

ляется выражением

где & комплексная

ES -

амплитуда напряженности электрического поля на поверхности элемента Гюйгенса.

Диаграмма направленности элемента Гюйгенса в главных плоскостях (a=0, a=p/2) опреде-

F (θ ,0) = F (θ ,π	) =	1 + cosθ	.	(5.12)

2	2

В полярной системе координат диаграмма направленности имеет вид

кардиоиды (рис.5.4), причем максимум излучения направлен вдоль оси z (θ=0).

119

Рис. 5.4

5.2 Примеры решения типовых задач

Задача №1 (поле диполя Герца)

Найти амплитуду тока в диполе Герца и излучаемую им мощность, если

его длина 5 см и в точке с координатами r = 1км, q = p¤2 амплитуда напря-

женности электрического поля Е	θ	=10-4 В/м. Частота колебаний
	θ
150 МГц.
Решение:
Определим излучаемую длину волны. Поскольку параметры среды не за-
даны, то будем полагать, что это –			воздух (или вакуум)
l = c			3 ×108 м
	=				с	= 2м.
	=					= 2м.
f		150 ×106 1
					с
Определим величину kr для оценки.			kr =	2π	r = p ×103 .
Определим величину kr для оценки.			kr =		r = p ×103 .
				l

Поскольку kr>>1, то точка наблюдения находится в дальней зоне и по-

ле определяется формулой (5.4).Запишем ее для амплитуды Еθ, опуская фазо-

вые множители i и e-ikr

E =	kI	стlW0	sinq . Отсюда I		=	4πrEθ	.
				ст
θ		4pr				klW0 sinq

120

Подставляя значения r , q и W0 = 120π Ом , получим амплитуду тока в ди-

поле I		=	1	А » 2.12 ×10−2 А.

	ст	15π

Сопротивление излучения диполя определяется формулой (5.6а)

	2πW		l	2
R =	0			= 5π 2 ×10− 2 » 0.5 Ом.

Σ	3	λ

Средняя по времени мощность излучения определится как

P	=	1	I	2	R	Σ	= 1.11 ×10−2	Вт.

Σ	2			ст

Задача №2 (поле диполя Герца)

Диполь Герца длиной 1м питается током частотой 1 МГц и амплитудой 2А. Определить напряженности электрического и магнитного полей на расстоянии 10м и 10 км и построить зависимости их амплитуд от углов θ и α при этих расстояниях.

Решение:

Аналогично решению предыдущей задачи, определим величины kr для двух значений r1=10м и r2=10км.

λ =

3 ×108

= 300 м,

2π

r » 0.209, kr

» 209 ,

106

Таким образом, расстояние r1

соответствует ближней зоне, а r2 – даль-

ней.

Поля в ближней зоне описываются формулами (5.3). При выполнении

расчетов учтем, что для воздуха

ωε

Hα =

lI ст

sinθ =

1 × 2

sinθ » 1.59 ×10

−3 sinθ А

4π102

4πr 2

= i

lIст

sinθ

= i

lIстW0

sinθ = i

sinθ » i2.86 sinθ

Eθ

4πωεr

4πkr3

= i

lIст

cosθ = i

lIстWo

cosθ = i

cosθ » i5.73cosθ

2πωεr 3

2πkr3

121

Таким образом, на расстоянии 10 м от диполя будут присутствовать две компоненты вектора E и одна – вектора H . Их диаграммы направленности в ближней зоне в полярной системе координат имеют вид

Рис. 5.5

На рисунке диполь выделен жирной линией. Следует обратить внимание на то, что в ближней зоне существует значительное продольное электрическое поле Еr и на сдвиг по фазе между полями Е и Н.

Поля в дальней зоне определяются формулами (5.4) . Определим амплитуду Hα

	kI		l		2	× 2 ×1
	kI	ст	l		π			−7 × sinθ А
Hα =		ст		sin θ =			sinθ = 3.33 ×10		.
Hα =	4πr			sin θ =			sinθ = 3.33 ×10		.
					300 ×	4π ×104		м
					300 ×	4π ×104

Электрическое поле имеет одну составляющую Еθ, которую можно опре-

делить согласно (5.9) через Нα и волновое сопротивление

E = W × H		α	=120π × 3.33 ×10−7	× sinθ =1.256 ×10−4 × sinθ В .
θ	0	α		м
				м

Диаграмма направленности в дальней зоне описывается функцией sinq и

имеет вид изображенный на рис. 5.5а для Нα или рис. 5.5б для Еθ.

Задача №3 (диаграмма направленности диполя над землей)

Определить диаграммы направленности в вертикальной и горизонталь-

ной плоскостях диполя Герца, находящегося над идеально проводящей землей на высоте h. Рассмотреть случаи вертикального и горизонтального диполей для высоты h= λ / 2 .

Решение:

122

Выберем прямоугольную систему координат для обозначения

z	M	z	M
	и		и

	h		h
			y	y
	б		б
	x		x
			Рис.5.6
	координат диполей и сферическую - для координат точки наблюдения
-			(рис. 5.6) Учет влияния идеально проводящей
-
+	+	-	земли на излучение антенн можно провести
+
			методом зеркальных изображений. Рассмот-
-	-		рим вертикальный и горизонтальные диполи,
-	-	+	расположенные над поверхностью идеально
+			расположенные над поверхностью идеально
+	Рис. 5.7		проводящей земли (рис.5.7)	Отметим для
	Рис. 5.7		проводящей земли (рис.5.7)	Отметим для

фиксированного момента времени на диполях положительные и отрицательные заряды и

соответствующие им заряды на зеркальных изображениях диполей. Покажем направление токов в диполях и их зеркальных изображениях от положительно-

го заряда к отрицательному. Видно, что токи в вертикальном диполе и его

зеркальном изображении имеют одинаковое направление, а в горизонталь-

ном – противоположное.

Перейдем к определению диаграмм направленности. Изобразим на рисун-

ке 5.8 условие задачи для вертикального диполя. В точке А расположен вер-

тикальный диполь, в точке В – его зеркальное изображение с таким же на-

правлением тока.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1912 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023118.93 Кб0Электромагнитная экология.-3.pdf
#
05.02.2023196.13 Кб3Электромагнитная экология..pdf
#
05.02.2023652.23 Кб17Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб13Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб45Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб18Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб37Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб41Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб50Электромагнитные поля и волны..pdf
#
05.02.20233.12 Mб25Электроника 1. Физические основы электроники-1.pdf
#
05.02.20231.01 Mб10Электроника 1. Физические основы электроники.pdf